§ 1. Делимость чисел

1. Сумма, разность и произведение двух целых чисел всегда целые числа. Этот факт иногда принято называть замкнутостью множества целых чисел по отношению к действиям сложения, вычитания и умножения.

По отношению же к действию деления множество всех целых чисел замкнутым не является: частное от деления одного целого числа на другое может, вообще говоря, и не быть целым.

Поэтому при изучении обстоятельств, связанных с делением целых чисел, одним из первых встает вопрос о выполнимости этого действия для данных двух чисел, т. е. о делимости этих чисел. При рассмотрении остальных арифметических действий над целыми числами подобный вопрос, очевидно, не возникает.

В дальнейшем мы будем считать известными основные свойства арифметических действий над целыми числами, а также простейшие свойства равенств и неравенств. Под "числом" всегда, если не оговорено противное, будет пониматься целое число.

Как обычно целые неотрицательные числа: 0, 1, 2, ... будут называться натуральными. Говоря о всех натуральных числах, мы будем пользоваться термином множество всех натуральных чисел.

Определение. Число а делится на число b (или, что то же самое, число b делит число а), если существует такое число с, что а = bс.

Этот факт называется делимостью числа а на число b и обозначается как аb.

Подчеркнем, что запись аb означает не какое-то действие, которое надлежит произвести над числами а и b, а некоторое утверждение, касающееся этих чисел. В зависимости от того, каковы числа а и b, утверждение a b может быть верным или неверным. Так, например, 42 верно, а 43 - нет.

Для выяснения того, является ли утверждение ab верным или нет, т. е. для выяснения делимости числа а на число b, имеется довольно много разно-образных способов. Один из них состоит в непосредственном делении числа а на число b. Однако такое деление часто оказывается слишком долгим и утомительным занятием, и естественно появляется желание установить истинность интересующей нас делимости, не производя фактического деления. Не лишним представляется и такое соображение: пока нас интересует только факт делимости числа а на число b; если же мы выполним деление, то мы попутно узнаем еще и частное от этого деления и остаток от него (если деление нацело "не получилось"); все эти числа, однако, для нас никакой ценности не представляют, так как мы в данный момент интересуемся только тем, будет ли остаток от деления равен нулю или нет. Значит, есть основания предполагать, что выполняя деление, мы какую-то (и по-видимому, немалую) часть работы потратили на получение "отходов производства". Можно надеяться, что более прямые способы выяснения делимости, чем "грубое" деление, которые не дадут нам столь обильных отходов, будут экономнее и позволят установить факт делимости более коротким путем. Эти надежды в действительности оправдываются, и такие способы выяснения делимости существуют. Они называются признаками делимости.

Некоторые признаки делимости, несомненно, известны читателю. Целью этой книжки является рас-смотрение различных признаков делимости, главным образом с принципиальной стороны.

Сущность всякого признака делимости на данное число b состоит в том, что при его помощи вопрос о делимости любого числа а на b сводится к вопросу о делимости на b некоторого числа, меньшего чем а. (Нетрудно видеть, что проверка делимости обычным делением также основана на этой идее.)

Таким образом, признак делимости является математическим объектом весьма распространенной, хотя и не бросающейся в глаза природы. Это не формула, не теорема, не определение, а некоторый процесс, совершенно такого же типа, что и процесс умножения чисел "столбиком" или, скажем, процесс вычисления одного за другим членов арифметической прогрессии.

Понятие признака делимости будет уточнено в следующем параграфе.

2. В определении делимости чисел ничего не говорится о том, сколько различных значений может иметь частное от деления а на b. Выясним здесь этот вопрос до конца, чтобы в дальнейшем к нему больше не возвращаться.

Пусть

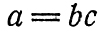(1.1)

и вместе с тем

Из этих равенств мы получаем

или

Если при этом b ≠ 0, то с - с' = 0, т. е. с - с'. Если же b = 0, то, очевидно, и a = 0, а равенство (1.1) выполняется при любом с.

Таким образом, на нуль делится только нуль, а частное от такого деления неопределенно. Именно это и имеется в виду, когда говорят о невозможности деления на нуль. Если же делитель отличен от нуля и делимость имеет место, то частное имеет одно, вполне определенное значение.

Говоря о делении, мы всегда будем предполагать делитель отличным от нуля.

Установим несколько простейших свойств делимости.

Теорема 1. аа.

Это свойство делимости называется ее рефлексивностью (или возвратностью).

Теорема 2. Если аb и b с, то с.

Это свойство делимости называется ее транзитивностью (или переходностью).

Теорема 3. Если аb и bа, то либо а = b, либо а = -b (антисимметричность делимости).

Теорема 4.Если аb и | b | > | а |, то а = 0.

Следствие. Если аb и а ≠ 0, то |а|≥|b|.

Теорема 5. Для того чтобы аb, необходимо и достаточно, чтобы | а || b |.

На основании этой теоремы в дальнейшем достаточно ограничиваться рассмотрением случая, когда делитель есть положительное число. Равным образом делимость произвольных целых чисел сводится к делимости неотрицательных чисел.

Теорема 6. Если а₁b, а₂b, ...., а_nb, то (а₁ + а₂ + .... +а_n)b.

Следствие. Если сумма двух чисел и одно из слагаемых делится на некоторое число b, то другое Слагаемое также делится на b.

Не следует считать все эти теоремы очевидными и не нуждающимися в каком-либо особом доказательстве. Дело здесь даже не в том, что в математике Доказательству подлежит всякое утверждение, кроме аксиом и определений. Доказательства этих фактов (например того, что всякое число делится на себя) принципиально необходимы, так как они не могут быть получены только из определения делимости, а нуждаются в использовании свойств самих чисел.

Подробнее в этом разобраться нам поможет следующий пример.

Очевидно, сумма, разность и произведение четных чисел всегда четны. Вместе с тем деление одного четного числа на другое не всегда выполнимо, а если и выполнимо, то частное не обязательно четно. Поэтому можно ввести понятие четной делимости четных чисел.

Определение. Четное число а четно делится на четное число b, если существует такое четное число с, что а = bс.

Очевидно, для четной делимости теорема 1 неверна, так как, например, не существует такого четного числа с, для которого а = ас.

К вопросам, связанным четной делимостью четных чисел, мы еще будем несколько раз возвращаться. Пример четной делимости показывает, что можно строить различные теории делимости с различными свойствами, и теоремы, верные для одних таких теорий, могут оказаться неверными для других.

Задачи. Доказать следующие утверждения:

1. 0: а.
2. а1
3. Если 1а, то а = 1.
4. Каково бы ни было а≠О, существует такое отличное от а число b, что ba.
5. Каково бы ни было число а, существует такое число b, что из bс и са следует либо с = b, либо с = а.
6. Доказать теоремы, аналогичные теоремам 2, 3, 4 и 5 для четной делимости.
7. Построить такую теорию делимости, в которой теоремы 1, 3 и 4 были бы верными, а теоремы 2 и 6 - нет.

3. Уже при самом беглом знакомстве с конкретными фактами делимости бросается в глаза следующее обстоятельство: возможности делимости чисел практически не связаны с их величиной. С одной стороны, существуют маленькие числа, которые делятся на сравнительно большое количество чисел. Например, 12 делится на 1, 2, 3, 4, 6 и 12; число 60 имеет 12 делителей. Таким богатым делителями числам можно противопоставить весьма большие числа, которые имеют минимальное число делителей - 2 (согласно теореме 1 и задаче 2, каждое отличное от единицы число делится хотя бы на два различных числа). Хотя в действительности и известны некоторые закономерности, связывающие свойства делимости чисел с их величиной, но эти закономерности носят столь сложный и запутанный характер, что мы не будем их здесь касаться.

4. Тем более интересным оказывается тот факт, что сама делимость позволяет установить среди чисел некоторый порядок, отличающийся от их обычного порядка по величине, но имеющий с ним много общего.

В самом деле, вдумаемся, какой точный смысл вкладывается в слова о возможности упорядочить натуральные числа по их величине. Под этой возможностью, как нетрудно видеть, понимается то, что для некоторых пар чисел а и b имеет место отношение "больше или равно":

которое означает, что разность а - b неотрицательна (т. е. должно существовать такое натуральное число с, что а - b + с). Но ведь и явление делимости состоит в том, что некоторые пары чисел а и b подчиняются некоторому, вполне определенному условию (именно, существует такое целое с, что а = bс)! Таким образом, отношение делимости и отношение "больше или равно" представляют собой понятия одной природы, и потому можно говорить об их общих свойствах или, наоборот, противопоставлять их друг другу.

В частности, подобно отношению делимости, отношение "больше или равно" между двумя натуральными числами является некоторым высказыванием об этих числах и может быть верным (например, 5≥3) или неверным (например, 3≥5).

Заметим сразу же, что отношение "больше или равно" имеет больше общих свойств с отношением делимости, чем отношение "больше". Это связано с тем, что отношение "больше или равно", подобно отношению делимости, рефлексивно (действительно, соотношение а 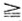а справедливо для любого а), а отношение "больше" рефлексивным не является (неравенство а > а не имеет места никогда). Именно поэтому здесь в качестве отношения порядка между натуральными числами рассматривается отношение "больше или равно", а не, казалось бы, более простое и естественное отношение "больше".

5. Отношение ≥ обладает следующими легко проверяемыми свойствами:

1° a ≥ а (рефлексивность).

2° Если а ≥ b и b ≥ а, то а = b (антисимметричность).

3° Если а ≥ b и b ≥ с, то а ≥ с (транзитивность).

4° Во всякой последовательности натуральных чисел a₁ ≥ a₂ ≥... ≥ a_n ..., все члены которой отличны друг от друга, найдется последнее число. Это свойство отношения иногда называется свойством полной упорядоченности множества натуральных чисел.

Свойство полной упорядоченности довольно сложно по формулировке и выглядит несколько искусственно. Однако оно вскрывает чрезвычайно важные черты в строении множества натуральных чисел, упорядоченных отношением ≥. Из него выводятся многие другие свойства этого отношения. Кроме того, мы увидим, что именно на нем основаны столь употребительные в разных вопросах математики рассуждения "по индукции".

В качестве полезного применения этого свойства отметим следующее: существует такое число а, что из а > b следует а = b (здесь а и b - натуральные числа).

В самом деле, если бы такого числа не было, то мы могли бы по каждому a_n находить такое a_n+1, что а_n ≥ а_n+1 и а_n ≠ а_n+1. Начав с произвольного a₁, мы получили бы последовательность

которая никогда не кончается. Но существование такой последовательности противоречит свойству полной упорядоченности множества натуральных чисел.

Таким образом, указанное число а действительно существует. Оно называется первым, или i, числом (очевидно, это нуль). Заметим здесь же, что мы Сейчас не установили единственности минимального числа. Эта единственность будет зафиксирована далее косвенном путем.

5° Каково бы ни было число а, существует отличное от а число b, для которого b≥.

Это свойство множества натуральных чисел называется его неограниченностью в смысле отношения

6° Каково бы ни было число а, не являющееся минимальным, существует такое b, что a≥b, a≠b, и для любого числа с из a≥c≥b следует либо с = а, либо с = b. Это формальное утверждение в переводе на содержательный язык означает, что каждое натуральное число, кроме 0, имеет непосредственно предшествующее натуральное число. (Иначе это можно сформулировать так: среди всех чисел, меньших данного, есть наибольшее.)

7° Либо a≥b, либо b≥а. Это свойство отношения называется его дихотомичностыо. В математике термин дихотомичность обычно выражает обязательную реализацию одной из двух возможностей. Само это слово греческого происхождения и означает разделение на две части.

Подчеркнем, что 1°-7° являются свойствами самого отношения на множестве всех натуральных чисел, а не свойствами тех или иных чисел, связываемых этим отношением. Поэтому может оказаться, что для какого-нибудь другого отношения, связывающего числа в пары, но не пз величине, а каким- либо иным способом, некоторые из утверждений 1°-7° могут оказаться и неверными.

Задача 8. Опираясь только на свойства 1°-7° отношения и не пользуясь никакими свойствами самих чисел и действий над ними:

а) Доказать единственность минимального числа;

б) Доказать единственность непосредственно предшествующего числа;

в) Сформулировать определение числа, непосредственно следующего за данным числом а (т. е. числа а + 1), и доказать его существование и единственность.

Задача 9. Проверить, какие из утверждений 1°-7° остаются в силе для отношения "больше" (>).

6. Справедливость свойств отношения ≥ (как впрочем, и любого другого отношения) может быть установлена двояко, Во-первых, мы можем воспользоваться свойствами тех или иных чисел или известными особенностями строения множества всех натуральных чисел. Именно так проверялись нами свойства 1° - 7°. Во-вторых, мы можем, уже убедившись в справедливости свойств 1° - 7 , отвлечься от того, что отношение ≥ связывает числа в пары и выводить дальнейшие свойства этого отношения только из его свойств 1°-7°. Так были нами доказаны существование минимального числа и утверждения задачи 8.

Второй подход к вопросу весьма употребителен в современной математике и носит название аксиоматического. При таком подходе устанавливаются некоторые аксиомы (в нашем случае ими являются утверждения 1° - 7°), которые отражают основные свойства изучаемых предметов и не подлежат доказательству, а из них чисто логическим путем, без повторного обращения к свойствам исследуемых предметов, выводятся все остальные утверждения, которые называются теоремами.

Быть может, некоторым из читателей рассмотрение свойств отношений в отрыве от связываемых этими отношениями объектов (например, чисел) покажется тем верхом математической абстракции, который в практической жизни совершенно не нужен. По этому поводу следует сделать два замечания.

Во-первых, с точки зрения современной математики все приводимые здесь рассуждения вовсе не являются "особенно абстрактными". Более того, в наши дни математикам приходится рассматривать одновременно много отношений и даже (!) связывать пары различных отношений новыми отношениями (так Сказать, отношениями "второго порядка").

Изложенный до сих пор материал позволяет проиллюстрировать понятие отношения между отношениями примером.

Пусть α, β, ... - некоторый набор отношений, связывающих натуральные числа. Это значит, что для любой пары чисел а и b и любого отношения у из нашего набора мы знаем, связывается ли пара а, b отношением у или нет. Если а и b отношением у связаны, будем писать aγb.

Будем говорить, что отношение α сильнее отношения β, и записывать это как α⊃β, если любая пара чисел, связанная отношением β, оказывается также связанной и отношением α, т. е. если из aβb следует aαb.

Так, например, обозначая отношение четной делимости через 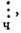мы можем написать 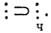. Далее, очевидно, что .

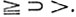Вместе с тем существуют естественные отношения на множестве натуральных чисел, относительно которых нельзя утверждать, что одно сильнее или слабее другого. Так, например, если для двух натуральных чисел а и b полагать 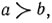, если последняя цифра в десятичной записи числа а больше последней цифры числа b, то 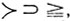ни ни .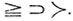

Конечно, для свободного оперирования столь сложными понятиями как отношения между отношениями необходима специальная тренировка.

Во-вторых, такие и даже еще более отвлеченные рассуждения все чаще и чаще начинают встречаться в приложениях математики к экономике, биологии, лингвистике, военному делу. К сожалению, более подробные пояснения на этот счет увели бы нас слишком далеко от основного предмета.

7. С упорядоченностью множества натуральных чисел отношением ≥ тесно связана возможность применять метод полной индукции (называемый также методом совершенной индукции или методом математической индукции). Обычно этот метод применяется в следующей форме. Пусть А(n) - некоторое утверждение, касающееся произвольного натурального числа n. Это, по существу, означает, что мы имеем дело с бесконечной последовательностью утверждений

о каждом из натуральных чисел. Предположим, что

а) справедливо утверждение A(0) ("основание индукции")^*;

б) из справедливости утверждений А (n) следует справедливость утверждения А(n+1) ("индуктивный переход").

^* (Часто за основание индукции принимают утверждение A(1). Очевидно, это различие не является существенным. Важно лишь, что основание индукции касается первого из рассматриваемых нами чисел.)

Принцип математической индукции утверждает, что в предположениях а) и б) А(n) справедливо для любого натурального n.

Принцип математической индукции не является каким-то самостоятельным утверждением, а может быть выведен из свойств 1° - 7° упорядочения множества натуральных чисел отношением

Действительно, предположим, что условия а) и б) принципа индукции для утверждений A(n) выполнены, но заключение этого принципа не имеет места. Последнее означает, что должны существовать такие числа m, для которых утверждение A(m) неверно. Пусть m₁ - одно из таких чисел. Если для всех я m₁ утверждение А (n) верно, то m₁ - наименьшее из чисел, для которых А (n) не имеет места. Если же A(n) верно не для всех n<m₁, то должно существовать такое m₂<m₁, что A(m₂) неверно.

В итоге мы приходим к некоторой последовательности различных чисел

для каждого из которых А(m) не имеет места. По свойству полной упорядоченности 4° в последовательности (1.2) должен быть последний член m_r. Очевидно, число m_r является наименьшим из всех чисел, для которых A(n) неверно.

Поскольку A(0) верно по условию, m_r ≠ 0, так что существует число m^*_r, непосредственно предшествующее m_r (в действительности этим числом является m_r - 1). Так как m^*_r < m_r утверждение A(m_r) должно быть верным. Но тогда по условию б) принципа математической индукции должно быть верным также и утверждение (m_r + 1), т. е. A(m_r), и мы получили противоречие. Это противоречие показывает, что нет чисел m, для которых A(m) не имело бы места (т. е. не было бы справедливо).

Сделаем следующее замечание. Проведенные только что рассуждения не следует считать ни доказательством принципа индукции, ни его основанием. Они означают лишь возможность вывода одного математического утверждения (метода индукции) из других (из свойств отношения ≥). Сами же эти свойства принимались нами в качестве аксиом, и потому не доказывались, а лишь проверялись. Всякая попытка их математического доказательства неизбежно натолкнулась бы на необходимость введения в качестве аксиом каких-то новых условий.

В частности, доказательства свойства полной упорядоченности должны использовать те же индуктивные рассуждения (читатель может в этом убедиться сам).

Методу математической индукции в его различных вариантах посвящены брошюры И. С. Соминского "Метод математической индукции" ("Наука", 1974) и Л. И. Головиной и И. М. Яглома "Индукция в геометрии" ("Наука", 1956), содержащие большое количество примеров применения этого метода. На протяжении данной книги этот метод также будет часто применяться.

Задача 10. Пусть пары объектов произвольной природы (ими могут быть числа, точки, функции, теоремы и т. д.) связываются некоторым отношением 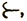обладающим свойствами, аналогичными свойствам 1° - 7°. Доказать, что тогда эти объекты (элементы) можно перенумеровать (т. е. выписать их в некотором порядке) A₁, A₂, A₃ ... так, что A_i 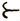A_j тогда и только тогда, когда i 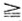j.

Сказанное, по существу, означает, что отношение, обладающее свойствами 1° - 7°, упорядочивает множество в линейную цепочку элементов:

8. Вернемся, однако, к отношению делимости. В случае положительных чисел теоремы 1, 2, 3 и задачи 3, 4 и 5 показывают, что в утверждениях 1°-6° мы можем заменить отношение 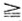отношением . Что же касается утверждения 7°, то в применении к делимости оно гласит: "из двух чисел хотя бы одно делится на другое".

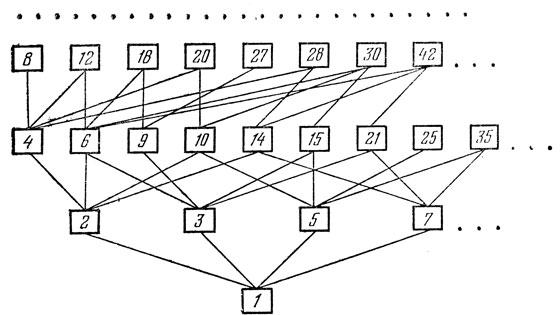
Но это неверно. Таким образом, отношение делимости обладает всеми свойствами отношения порядка за исключением одного. В связи с этим отношение делимости упорядочивает натуральные числа не в виде линейной цепочки, а иным, более сложным образом (см. рисунок). Заметим, что числа, близкие по величине, могут оказаться довольно "далекими" друг от друга в смысле делимости. Наглядно демонстрируют это числа 4 и 5 или 7 и 8,

Попробуем от делимости целых положительных чисел перейти к делимости чисел натуральных, т. е. включим в рассмотрение нуль. Тогда схема на рисунке пополнится клеткой, лежащей выше всех остальных клеток схемы, ибо нуль делится на любое число и ни одно из чисел, отличных от нуля, на нуль не делится.

Читателю предоставляется самостоятельно переформулировать и проверить утверждения 1° - 7° для этого случая.

9. Определение. Любое отношение 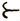подчиненное условиям:

1° рефлексивности 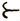(а а):

2° антисимметричности (из а 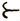b и b 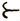а следует а = b);

3° транзитивности (из а b и b с следует а с),

называется частично упорядочивающим отношением. Частично упорядочивающие отношения играют большую роль там, где "настоящее", линейное упорядочение не имеет места, например там, где каждый объект описывается или оценивается по нескольким различным, качественно несравнимым между собой показателям.

В качестве примера можно привести оценку результатов спортивных соревнований по нескольким различным видам спорта. Если одна из команд заняла по всем видам программы соревнований более высокие места, чем другая, то естественно считать, что первая команда добилась больших успехов. Если же эти более высокие места были заняты по всем видам программы, за исключением, скажем, игры в крокет (которая почему-то на этот раз оказалась включенной в программу соревнований), где вторая команда оказалась сильней, то вопрос об окончательном распределении мест между нашими командами оказывается уже не столь очевидными. Энтузиасты игры в крокет могут даже настаивать на более высоком месте для второй команды. Во всяком случае любое суммарное распределение мест должно быть связано с некоторыми условными пересчетами (например, с приписыванием очков).

10. Условия 1°-3°, соблюдение которых делает отношение 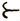отношением частичного упорядочения, являются довольно свободными. Поэтому частично упорядоченными и притом упорядоченными весьма различными способами могут быть самые разнообразные объекты. В связи с этим о произвольном частично упорядочивающем отношении мало что можно сказать сверх того, что оно частично упорядочивающее. В частности, к объектам, для которых определено частично упорядочивающее отношение, нельзя, вообще говоря, применить метод математической индукции.

Дополним, однако, условия 1° - 3° следующими:

4° полная упорядоченность;

5° неограниченность;

6° каждый объект, отличный от минимального, имеет непосредственно предшествующий;

8° каждый объект имеет не более конечного числа предшествующих;

9° каковы бы ни были а и b 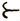a (b ≠ a), существует такое с, непосредственно предшествующее b, что с 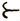а.

Оказывается, что на основе частичной упорядоченности множества натуральных чисел отношением, которое удовлетворяет условиям 1°-6°, 8° и 9°, можно построить некоторое видоизменение метода индукции, состоящее в следующем.

Пусть снова А(n) - утверждение, касающееся произвольного числа n. Предположим, что

а) Справедливо утверждение А (а), где а есть минимальное число в смысле упорядочения ;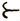

б) Если n - некоторое число, и справедливость всех утверждений вида А (m) для всех таких m, что n 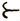m и n ≠ m, установлена, то верно и утверждение А(n).

Новая форма принципа индукции утверждает, что при соблюдении условий а) и б) утверждение А(n) справедливо при любом n.

Задача 11. Вывести "новую форму" принципа индукции из ее "старой формы".

Так как отношение делимости условиям 1° - 6°, 8° и 9° удовлетворяет (сформулируйте и проверьте для отношения делимости условия 8° и 9°), этот принцип индукции к отношению делимости применим.

В применении к делимости новый принцип индукции может быть сформулирован так: если некоторое утверждение А(n) справедливо при n = 1 и из справедливости его для всех делителей числа n, отличных от n, следует его справедливость для n, то оно имеет место для любого числа.

11. Деление целых чисел, как мы видели, выполнимо не всегда. Поэтому целесообразно наряду с действием деления рассматривать и другое, более общее действие, которое всегда выполнимо, а в случае выполнимости действия деления, по существу, совпадает с ним. Таким действием является деление с остатком.

Определение. Разделить число a на число b (b > 0) с остатком - значит представить число а в виде

где 0 ≤ r < b.

Число q при этом называется неполным частным, а число r - остатком от деления а на b. Очевидно, r = О тогда и только тогда, когда а b. В этом случае q равно частному от деления а на b.

Покажем, что деление с остатком всегда выполнимо, а неполное частное и остаток вполне определяются делимым и делителем, т. е. единственны.

Пусть сначала а 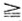0. Будем выписывать одно за другим числа

до тех пор, пока не появится отрицательное число (очевидно, рано или поздно такое число должно по-явиться^*). Пусть последним из неотрицательных членов последовательности (1.3), т. е. самым маленьким из них, окажется число а - bq.

Обозначая его через r, мы имеем

^* (Точнее говоря, это следует из полной упорядоченности множества натуральных чисел отношением )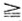

Очевидно, r < b (иначе бы число r - b, т. е. a - (q + 1 )b, было бы неотрицательным, а этого не может быть, так как r - наименьшее из неотрицательных чисел среди (1.3)). Таким образом, (1.4) и является искомым представлением числа a.

Пусть теперь а < 0. Рассуждая аналогично предыдущему, будем выписывать последовательность чисел

до тех пор, пока не появится первое неотрицательное число r (легко проверить, что r < b). Пусть

Тогда, обозначая -q' через q, мы получаем

а это и требовалось.

Возможность деления с остатком доказана во всех случаях.

Докажем теперь однозначность этого деления, т. е., что из

и

следует

От такого доказательства единственности нельзя отмахнуться попросту, заявив, что так как, дескать, действие вычитания однозначно, последовательность (1.3) может быть построена единственным способом; последний ее неотрицательный член также вполне определен; пусть это будет наше r ... и т. д. Такое рассуждение еще не избавляет нас от возможности получить другие значения q и r каким-нибудь совершенно иным путем.

Сопоставляя отношения (1.5) и (1.6), мы видим,

что

откуда

т. е. r - r₁ делится на b. Но |r - r₁| < b, а по теореме 4 это возможно лишь при

т. е. при r = r₁. Но тогда

и ввиду неравенства нулю числа b

т. е. q₁ = q. Однозначность деления с остатком доказана. Таким образом, нами доказана следующая теорема.

Теорема 7 (о делении с остатком). Для произвольных чисел a и b (b > 0) существуют и единственны такие числа r и q, что

причем 0 ≤ r < b.

Заметим, что в частности при b = 1 должно быть r = 0, откуда a = q. Это соответствует утверждению задачи 2. Ясно вместе с тем, что если b > 1, то а > q.

Задача 12. Сформулировать и доказать теорему о делении с остатком для четной делимости.

12. Определение. Число р, не равное единице, называется простым, если оно делится только на себя и на единицу.

Простыми числами являются, например, числа 2, 3, 5, 7, 11, 13 и т. д.

Число, отличное от единицы и не являющееся простым, называется составным.

Теорема 8. Простых чисел бесконечно много.

Всякое число, делящее одновременно числа а и b, называется общим делителем этих чисел. Наибольший из общих делителей чисел а и b называется их наибольшим общим делителем и обозначается обычно через (а, b).

Если наибольший общий делитель чисел а и b равен единице, то эти числа называются взаимно простыми.

Иначе говоря, числа а и b называются взаимно простыми, если они одновременно не делятся ни на какое число кроме единицы.

Теорема 9.Если a и p - натуральные числа, причем число р простое, то либо a р, либо числа a и р взаимно просты.

Всякое число, делящееся одновременно на числа а и b, называется общим кратным этих чисел. Наименьшее положительное общее кратное а и b называется наименьшим общим кратным этих чисел.

Теорема 10. Если М - общее кратное а и b, а m - их наименьшее общее кратное, то М m.

Теорема 11. Наименьшее общее кратное двух взаимно простых чисел равно их произведению.

Следствие. Для того чтобы число а делилось pa взаимно простые числа b и с, необходимо и достаточно, чтобы оно делилось на их произведение.

Теорема 12.Если ab с, причем числа b и с взаимно простые, то а с.

Теорема 13. Если произведение нескольких сомножителей делится на простое число р, то хотя бы один из сомножителей делится на р.

Следствие. Если р - простое и 0 < k < р, то число

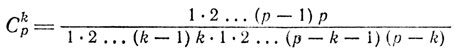
делится на р.

Теорема 14 (основная теорема арифметики). Всякое целое положительное число, кроме единицы, может быть представлено в виде произведения простых сомножителей и притом единственным способом (произведения, отличающиеся только порядком сомножителей, различными не считаются).

Основная теорема арифметики указывает на принципиальную возможность разложения любого числа на простые сомножители. Однако практическое осуществление такого разложения встречает большие трудности, которые современная математика иногда еще не может преодолеть. Разложение больших чисел на множители или установление их простоты в настоящее время осуществляется на основе применения Электронных вычислительных машин. Так, лишь совсем недавно было обнаружено, что число 2¹⁹⁹³⁷-1 является простым.

Пусть некоторое число а разложено в произведение простых сомножителей. Объединяя равные сомножители, мы получим формулу вида

где р₁, р₂,...., p_r - различные простые числа, α₁, α₂,...,α_r - некоторые целые положительные числа. Произведение, стоящее в правой части формулы (1.7), называется каноническим разложением числа а.

Теорема 15. Для того чтобы числа а и b были взаимно простыми, необходимо и достаточно, чтобы ни один из простых сомножителей, входящих в каноническое разложение числа а, не входил в каноническое разложение числа b.

Теорема 16.Пусть (1.7) - каноническое разложение числа а. Тогда для делимости b а необходимо и достаточно, чтобы

b p₁^α₁, bp₂^α₂,....,bp_r^α_r

Из теорем 15 и 16 вытекает, что делимость на произведение нескольких взаимно простых чисел равносильна одновременной делимости на каждое из них.

Задача 13. Оценить сверху наименьший простой делитель составного числа a.

Теорема 17. Пусть

a = p₁^α₁p₂^α₂...p_r^α_r

- каноническое разложение числа а. Тогда для делимости а b необходимо и достаточно, чтобы каноническое разложение b имело вид

b = p₁^β₁p₂^β₂...p_r^β_r

где

Весьма важным для целей данной книги оказывается следующий факт.

Теорема 18. Пусть m и t - натуральные числа. Тогда m можно представить в виде такого произведения m = m_lm₂, что (m₁, t) = 1 и найдется такое k, для которого t^k m₂.

Этот факт имеет свои далеко идущие алгебраические аналогии, но мы их затрагивать не будем.

Задача 14. Указать способ построения по каноническим разложениям двух чисел канонических разложений наименьшего общего кратного этих чисел и их наибольшего общего делителя.

Задача 15. Обозначим через τ(а) число различных делителей числа a (включая единицу и само число a). Показать, что для числа а с каноническим разложением p₁^α₁p₂^α₂...p_r^α_r

Задача 16. Найти а, если известно, что а 3, а 4 и τ(а) = 14.

Задача 17. Каноническое разложение числа а имеет вид p₁^α₁p₂^α₂ и τ(а²) = 81. Чему равно τ(а³)?

Задача 18. Чему равно а, если а = 2τ(а)?

Задача 19. Доказать, что каково бы ни было К > 0, найдется такое натуральное число k, что для всякого числа а, имеющего k простых сомножителей, будет

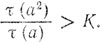
Задача 20. Верны ли для четной делимости аналоги теорем 11-14?