Глава XII. Часто или редко?

Рассматривая эратосфеново решето, мы видим, что сначала промежутки между последовательными простыми числами невелики, но по мере продвижения в ряду натуральных чисел, они, как правило, становятся больше и больше. Иными словами, по мере движения вдоль ряда натуральных чисел, простые числа встречаются всё реже и реже (см. таблицу в конце этой книжки). Если среди чисел первого десятка мы находим четыре простых числа, то между 1001 и 1010 имеется только одно: 1009.

Число и наука о нем

Евклид доказал, что простых чисел бесконечно много: как бы далеко мы ни зашли в натуральном ряду, нам будут попадаться простые числа. С другой стороны, "острова", состоящие сплошь из составных чисел, будут, как правило, становиться "длиннее", простые числа будут встречаться реже и реже. Каков же закон распределения простых чисел? Как узнать, например, сколько их содержится между 1000000 и 10000000, не пересчитывая их непосредственно? Эта задача принадлежит к числу труднейших, и до сего времени до конца она не решена. Сложность задач, связанных с распределением простых чисел, стала у математиков поговоркой. О ней знают и нематематики. Даже поэты упоминают о ней. Валерий Брюсов писал в одном из своих известных стихотворений:

...Но пред Эдипом загадка Сфинкса: 
Простые числа всё не разгаданы...

Разберём пример, который позволит лучше освоиться с самой постановкой вопроса. Рассмотрим бесконечную геометрическую прогрессию:

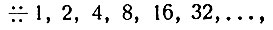
где каждое последующее число в два раза больше предыдущего. Число членов здесь бесконечно. Как же расположены эти числа по отношению к ряду всех натуральных чисел? Легко видеть, что вначале они "сидят" очень густо. В промежутке от 1 до 10 мы имеем четыре таких числа (1, 2, 4, 8). В промежутке от 30 до 40 мы имеем уже только одно (32). Наконец, в промежутке от 1025 до 2025 (промежуток в целую тысячу) нет ни одного числа нашего ряда. Нетрудно показать, что если зайти в натуральном ряду достаточно далеко, то можно найти сколь угодно длинный числовой промежуток ("остров"), не содержащий ни одного члена нашей прогрессии.

Всё это очень напоминает свойства простых чисел. Но есть и существенная разница. Закон распределения чисел ряда 1, 2, 4, 8, 16,... в ряду натуральных чисел очень прост. Нетрудно написать формулу, позволяющую найти число членов этого ряда между двумя любыми натуральными числами. Действительно, число членов нашего ряда, не превосходящих числа N, равно увеличенной на единицу целой части двоичного логарифма числа N (читатель, знакомый с логарифмами, сам докажет это). Наоборот, закон распределения чисел ряда

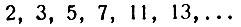
(простых чисел) необычайно сложен: за длинной серией составных чисел может последовать серия, богатая простыми числами. Например, после промежутка в 11 составных чисел

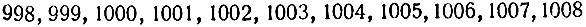
следует промежуток

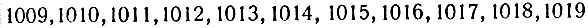
тоже из 11 чисел, содержащий три простых: 1009, 1013 и 1019.

Л. Эйлер

Мы видели, что промежутки между простыми числами остановятся всё больше и больше и делаются в конце концов сколь угодно длинными. Но встречаются, и тоже достаточно далеко, неожиданные "сгустки" простых чисел. По соседству с тысячей, например, вслед за промежутком в 11 составных следует серия из 11 чисел, из которых 3 простые. Значит, на 22 числа приходится три простых - более 13 процентов, что совсем не так уж мало! Далее, есть основания полагать, что в ряду натуральных чисел как угодно далеко встречаются пары соседних простых чисел - "числа-близнецы", о которых уже упоминалось в предыдущей главе. Поэтому наличие огромных "островов", свободных от простых чисел, почти ничего не даёт нам для суждения о том, насколько часты последние среди всех натуральных чисел. И всё-таки... И всё-таки уже Эйлер (1707-1783 гг.), замечательнейший математик XVIII столетия, полагал, что простые числа встречаются "бесконечно реже, чем целые". Как понимать эти слова Эйлера? Они означают следующее: рассмотрим какое-нибудь натуральное число N, простое или составное. Рассмотрим все простые числа, не превосходящие N, т. е. числа

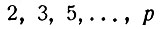
(если N простое, то последним в этом ряду будет само N = p, в противном случае - некоторое число (простое), меньшее N). Допустим, что всего будет n простых чисел, не превосходящих N. Если, например, исходить из N = 10, то простыми числами, меньшими чем 10, будут 2, 3, 5,7; таких чисел будет всего 4; значит, в этом примере n = 4. Читатель сам подсчитает, что при N = 19 n = 8; при N = 30 n = 10 и т. д.

Само число n мало что даёт для интересующей нас задачи, но отношение 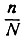как раз и показывает, какую долю составляют простые числа, не превосходящие данного числа, по отношению ко всем натуральным числам, его не превосходящим. Отношение 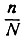вполне характеризует густоту, или, выражаясь научным языком, "плотность" простых чисел среди натуральных. В следующей таблице приведён ряд значений N и соответствующих значений n и 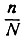. В последней строке показано, какой процент составляет число n по отношению к N:

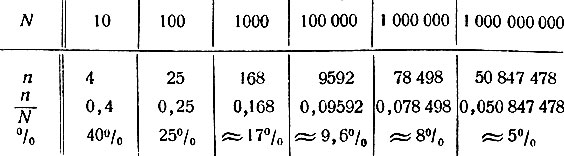
(Значок ≈, поставленный перед некоторыми числами последней строки, заменяет слово "приблизительно"; например, ≈17% читается: "приблизительно 17 процентов".) Мы видим, что "плотность", густота простых в ряду всех натуральных чисел становится меньше и меньше, если мы рассматриваем всё большие и большие числовые промежутки. Слова Эйлера о том, что простые числа встречаются бесконечно реже, чем целые, надо понимать так: если рассматривать очень большое количество N последовательных натуральных чисел, то отношение 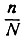будет очень малым числом; точнее, если мы выберем какое-нибудь очень малое значение для 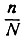, например одну миллионную, одну миллиардную и т. д., то всегда можно будет найти такое большое натуральное число, что при всех значениях N, которые его превосходят, наше требование будет выполняться, т. е. 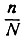будет меньше, чем указанная малая дробь.

Сам Эйлер доказал своё утверждение не вполне строго. Первое безупречное доказательство этого факта придумал французский математик А. М. Лежандр, опубликовавший его в 1798 г. Таким образом, вопрос о плотности простых чисел был решён в том смысле, что удалось установить неограниченное убывание этой плотности при возрастании числа N.

Установив это, математики поставили задачу-научить-рея вычислять n по данному N. Иными словами, они задались целью найти аналитическое выражение (формулу) количества простых чисел, не превосходящих данного натурального числа.

Эту задачу средствами современной математики решить ещё не удалось. Тогда её заменили двумя другими задачами: во-первых, ст ли искать формулу для отыскания n по заданному N не точную, а приближённую, но такую, чтобы при больших N ошибка была ничтожно мала, и тем меньше, чем больше N; во-вторых, пытались найти те закономерности, которым подчиняются самые уклонения истинного закона распределения простых чисел от этой формулы. Обеим этим задачам уже полтораста лет, и занимались ими лучшие математики и за границей и у нас.

Первую простую формулу, приближённо выражающую число простых чисел, меньших, чем заданное натуральное число N, дал Лежандр; он получил её "путём подбора", причём она достаточно хорошо давала n для любых N, больших чем 1000 и меньших чем 400000. (Во времена Лежандра таблицы простых чисел были составлены только до N=400000; в наше время эратосфеново решето доведено до N=9000000.)

Вот формула Лежандра:

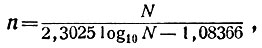
причём берётся, разумеется, целая часть неправильной дроби, вычисленной по этой формуле. Рассмотрим табличку, дающую соответствующие различным N значения n, вычисленные по формуле Лежандра и подсчитанные непосредственно по таблице:

Начиная с N= 1000 "наблюдённые" и вычисленные значения п очень близки друг к другу, причём уклонения получаются "двусторонние": при некоторых значениях N "наблюдённое" значение чуть больше вычисленного, при других -чуть меньше. Доказать справедливость формулы Лежандра в общем виде не удалось ни ему самому, ни другим математикам.

Л. Дирихле

В середине прошлого века интерес к проблемам Теории Чисел в значительной мере усилился. Крупную роль сыграли работы Л. Дирихле (1805-1859 гг.). Дирихле работал, главным образом, в области Математического Анализа (так называются главы математики, посвящённые изучению непрерывно изменяющихся величин: интегральное исчисление, дифференциальное исчисление и т. п.). Но попутно он занимался и Теорией Чисел и, прилагая к ней последовательно методы анализа (в этом - его большая заслуга), получил ряд интересных результатов. Мы говорили уже, что он доказал справедливость Великой теоремы Ферми при n = 5 и n = 14 и что им же доказано наличие бесконечного множества простых чисел в любой арифметической прогрессии со взаимно-простыми первым членом и разностью. Им же были получены важные результаты в учении о неопределённых уравнениях второй степени. С лёгкой руки Дирихле^* математики разных стран начали применять аналитические методы к изучению натуральных чисел.

^* (Дирихле первый стал систематически применять к изучению натуральных чисел методы анализа непрерывных величин. Но отдельные результаты на этом пути получили до него Эйлер и Гаусс.)

Французский математик Бертран, исходя из "опытов" с эратосфеновым решетом, высказал предположение, что между любым числом и числом, вдвое большим, имеется по крайней мере одно простое число. (Точнее, если 2x>7, то между х и 2х - 2 всегда имеется простое число.) Он не сумел доказать это предложение, но, опираясь на него, доказал ряд важных теорем арифметики и алгебры. Предложение о том, что между числами х и 2х (при х>1) имеется по крайней мере одно простое число, получило у математиков наименование "постулата Бертрана"^*. Доказать постулат Бертрана удалось в 1852 г. Чебышеву.

^* (Латинское слово postulatum (постулатум) значит "требование". В старых руководствах формулировка аксиом обычно начиналась словами: "потребуем, чтобы...".)

Пафнутий Львович Чебышев (1821-1894 гг.) по справедливости считается гордостью русской науки. Полвека работал он в самых разнообразных областях математики и везде получил выдающиеся результаты. Но самое важное в его деятельности - то, что он ставил совершенно новые вопросы, быстро привлекавшие к себе внимание многих математиков, в первую очередь - его учеников. Он создал русскую математическую школу, представители которой до сих пор занимают ведущее положение в науке.

П. Л. Чебышев

Учёные всего мира признали и оценили заслуги Чебышева. Английский математик Сильвестр писал в 1881 г., что для дальнейших успехов Теории Чисел нужно ждать, пока родится некто, настолько же превосходящий Чебышева своею проницательностью и вдумчивостью, насколько Чебышев превосходил этими качествами обыкновенных людей. Немецкий математик Ландау писал в 1909 г.: "Первый после Евклида, кто пошёл правильным путём для решения проблемы о простых числах и достиг важных результатов, был Чебышев". Чтобы почувствовать всю значительность этой оценки, нужно вспомнить, что Чебышева отделяют от Евклида 22 века и что в эти веки жили Ферма, Эйлер и Гаусс!

Чебышеву не удалось найти формулу, которая позволяла бы по данному N точно находить соответствующее значение "плотности" 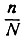. Мы говорили уже, что и теперь, спустя сто лет после работ Чебышева по теории чисел, эта задача считается неразрешимой (средствами современной науки, разумеется: наука будущего, безусловно, её решит). Но Чебышев доказал, что при очень больших значениях N отношение 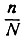мало отличается от величины 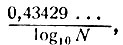причём точность формулы тем больше, чем большие значения N рассматриваются. Такого рода формулы, справедливые только приблизительно, но дающие тем большую точность, чем больше значения входящих в них величин, носят название асимптотических формул. Значит, можно сказать, что Чебышев дал асимптотическую формулу для плотности распределения простых чисел. Ему же удалось дать асимптотическую формулу для вычисления самого числа n простых чисел, не превосходящих данного N, но в эту формулу входит знак интеграла, и мы приводить её здесь не будем.

Чебышев справедливо считается создателем асимптотических законов распределения простых чисел. У него был, правда, предшественник, который чисто "опытным" путём - путём внимательного изучения эратосфенова решета - нашёл те же формулы, но доказать их правильности он не сумел и не публиковал их. Это был Гаусс.

После открытия асимптотических формул стал вопрос об оценке их точности и о тех закономерностях, которые можно подметить в самом уклонении "наблюдённых" значений числа n от вычисленных по этим формулам. Подобного рода вопросами занимались и сам Чебышев, и Адамар, и Ландау, а в последнее время - английские математики Гарди и Литтлвуд. Вопрос об отклонениях от формул Чебышева оказался чрезвычайно трудным. Но и здесь кое-что удалось сделать.

В приводимой здесь таблице в первой строке, отмеченной буквой N, даны значения натуральных чисел, а во второй, отмеченной буквой А,- соответствующие им значения для n, вычисленные по формуле Чебышева; наконец, в третьей строке - точные значения n

Мы видим, что разница между Липе ростом N возрастает, но доля, которую эта разница составляет от числа N, убывает и убывает быстро. При N = 1000, например,

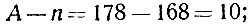
это 10 составляет ¹/₁₀ процента от тысячи. При N = 1 000000 будем иметь

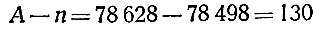
(больше чем при N = 1000); но эти 130 по отношению ко всему рассматриваемому миллиону составляют лишь 0,013 - почти в 8 раз меньше, чем в случае N = 1000. Именно это отношение характерно для оценки качества приближённого соотношения. Мы видим, что для формулы Чебышева это отношение очень мало; стало быть, она хороша: чем больше рассматриваемые числа, тем эта формула лучше (асимптотический закон).

С другой стороны, мы замечаем, что А всегда больше n, и это справедливо не только для чисел, помещённых нами в табличку, но и для всех чисел N, для которых были подсчитаны соответствующие им А и n. Казалось естественным ожидать, что формула Чебышева даёт всегда несколько "завышенный" результат. До 1914 г. было много попыток доказать это утверждение, т. е. доказать, что А>n при любом N. Но в 1914 г. Литтлвуд показал, что существуют такие числа (такие значения N), при которых n должно быть обязательно больше А, причём в дальнейшем при ещё больших значениях N будут встречаться и такие N, при которых А>n, и такие, при которых n>А; иными словами, уклонения от чебышевской формулы будут не только ничтожно малы, но будут носить совершенно случайный характер, давая результат, то чуть-чуть больший, то чуть-чуть меньший истинного.

Каково же то наименьшее натуральное число, для которого чебышевская формула даёт результат, меньший чем нужно? Товарищ Литтлвуда по работе, математик Гарди, показал, что это число невероятно велико. Оно не меньше чем 10⁷⁰⁰. Казалось при этом, что подойти как-то ближе к этому числу невозможно. И только совсем недавно, в 1933 г., английскому математику Скьюзу удалось показать, что (если сделать некоторые дополнительные предположения) можно оценить то число, при котором впервые в числовом ряду чебышевская формула даёт результат, меньший истинного. Это число равно приблизительно 10¹⁰¹⁰³⁴.

Громадность числа, данного Скьюзом, превосходит всё, что только можно себе представить. Разумеется, мы, пользуясь бесконечностью ряда натуральных чисел, без труда напишем числа, ещё - много большие, например, число, подобное скьюзовскому, но имеющее пять "этажей".Однако это будут "призраки, лишённые плоти и крови", потому что они не связаны ни с какой конкретной задачей. Число же Скьюза получилось в результате решения важной проблемы, естественно выдвинутой наукой, и в этом смысле оно является "числом-рекордсменом", оставившим далеко позади всех своих конкурентов. Число Курта Лассвица, число 9⁹⁹, о которых говорилось в первой главе, даже неизмеримо огромное число 10^8*1016, до которого дошёл в своём Псаммите Архимед, неизмеримо малы рядом со скьюзовским гигантом...