Глава XIII. Проблема Гольдбаха

В предыдущей главе мы познакомились с вопросом распределения простых чисел среди всех натуральных. Оказалось, что простые числа, расположенные сравнительно густо в начале натурального ряда, в дальнейшем становятся всё реже и реже, промежутки между ними становятся всё больше и больше. В этих промежутках попадаются числа, представляющие собою сумму двух простых чисел. Вот, например, числа первого десятка: 1 (в счёт не идёт); 2 (простое); 3 (простое); 4(4 = 2 + 2 - сумма двух простых); 5 (простое); 6(3 + 3 - сумма двух простых); 7 (простое); 8 (3 + 5 - сумма двух простых); 9 (2 + 7 - сумма двух простых); 10 (3 + 7 - сумма двух простых). Мы видим, что все числа первого десятка или являются простыми, или представляют собой сумму двух простых. Но уже 27 представить в виде такой суммы не удаётся. Зато 27 можно записать как сумму трёх простых слагаемых: 27 = 3 + 11 + 13. Спрашивается, для какого натурального числа трёх простых слагаемых не будет уже достаточно? Какое наименьшее число будет суммой не меньше, чем четырёх, пяти и т. д. простых слагаемых?

Число и наука о нем

Подобные задачи можно ставить применительно не только к простым числам. Математиков давно интересует вопрос, как заданное число записать в виде суммы некоторого числа квадратов. Если это возможно, то сколькими способами осуществляется разложение? Те же вопросы можно поставить для разложения числа на сумму кубов и т. д. Возникает своеобразная область Теории Чисел, в которой вместо делителей и множителей приходится иметь дело со слагаемыми и суммами. Её называют аддитивной теорией чисел, производя название от латинского слова additio (аддицио), что значит "сложение". Что касается той части Теории Чисел, которая имеет дело с множителями и делителями (учение о делимости и т. д.), то она носит название мультипликативной теории чисел (от латинского multiplicatio - мультипликацио,- что значит "умножение").

Вернёмся к простым числам, именно к задаче о представлении любого числа в виде суммы некоторого количества простых. Этой задачей более двухсот лет тому назад занялся член Петербургской Академии наук Хр. Гольдбах. Он перепробовал очень много чисел, пытаясь разложить их на сумму простых, и пришёл к убеждению, что трёх слагаемых всегда достаточно. Не сумев доказать это предложение, не найдя даже путей к доказательству, он написал о. нём своему другу Эйлеру, с которым уже без малого 15 лет переписывался и который был тогда в зените славы. В письме от 7 июня 1742 г. Гольдбах сообщил Эйлеру, что рискует высказать следующее предположение: "любое число, большее пяти, представляет собой сумму трёх простых". Эйлер ответил, что считает безусловно верной теоремой утверждение, что каждое чётное число есть сумма двух простых. Отсюда, как простое следствие, получается утверждение Гольдбаха (почему?). Впрочем и Эйлер доказательства не дал.

Итак, поставлена следующая задача (её называют "проблемой Гольдбаха"): требуется доказать или опровергнуть предложение: "всякое число, большее единицы, является суммой не более трёх простых чисел". Ни современники Гольдбаха и Эйлера, ни даже математики прошлого - XIX - столетия почти ничего не смогли сделать для решения этой задачи. Правда, Г. Кантор, один из оригинальнейших математиков прошлого века, терпеливо перепробовал все чётные числа от 2 до 1000, а Обри - от 1000 до 2000; они убедились, что в этих пределах любое чётное число является суммой двух простых. В 1911 г. Е. Меле показал, что подавляющее число чётных чисел от 4 до 9 000 000 являются суммами двух простых; исключений может быть не больше четырнадцати (т. е. для 4499 986 чётных чисел утверждение Гольдбаха наверняка справедливо). Наконец, на рубеже XX века появляется ряд работ, пытающихся наметить пути решения этой проблемы или связать её с другими задачами математики. Но для строгого её доказательства ничего сделать не удалось, и в 1912 г. крупнейший знаток теории чисел Э. Ландау высказал на международном конгрессе математиков предположение, что эта задача средствами современной математики вообще неразрешима!..

В 1923 г. двум английским математикам - Гарди и Литтлвуду, о которых мы уже говорили, - удалось добиться некоторого сдвига в попытках найти решение гольдбаховской задачи. Им удалось связать проблему Гольдбаха с одной из труднейших и интереснейших задач специальной главы высшей математики, называемой теорией аналитических функций. Эта задача тоже до конца не решена, но открывшаяся связь между двумя, казалось бы, разнородными ветвями науки, оказалась плодотворной и привела к ряду открытий.

Решительный перелом наступил в 1930 г. Советскому математику Льву Генриховичу Шнирельману (1905-1938 гг.), талантливому учёному, удалось так видоизменить задачу, что с помощью им же придуманных путей он сумел её решить. Именно, видя бесплодность попыток доказать утверждение Гольдбаха в его первоначальном виде, Шнирельман поставил родственную ей задачу, на вид более сложную, но по существу значительно более простую. Он, как говорят математики, "ослабил" требования задачи Гольдбаха. Гольдбах требует, чтобы каждое натуральное число являлось суммой не более трёх простых. Можно потребовать, чтобы каждое натуральное число, было суммою не более четырёх, пяти,..., ста простых. Эти требования, очевидно, слабее гольдбаховских: число, разложимое в сумму ста, может не разлагаться в сумму трёх простых.

Л. Г. Шнирельман

Наконец, можно, что и сделал Шнирельман, поставить вопрос так: существует ли какое-то вполне определённое, но нам неизвестное целое число (обозначим его буквою С), такое, что любое натуральное число можно представить в виде суммы не более чем С простых слагаемых?

Иными словами, каково бы ни было натуральное число N, всегда можно написать

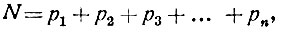
где р₁, р₂,...,p_n - простые числа, а n наверное меньше (или в крайнем случае равно) С. Если удастся доказать, что С = 3, то утверждение Гольдбаха будет доказано. Эту "ослабленную" теорему Гольдбаха Шнирельману удалось доказать полностью. Само, пока неизвестное, число С с тех пор называют "числом Шнирельмана" или "константой Шнирельмана" (слово constanta - константа - значит по-латыни "постоянная"). Значит, утверждение Гольдбаха можно сформулировать и так: "константа Шнирельмана равна трём". Но этого мало. Самый точный анализ метода Шнирельмана, сделанный разными математиками (Романов, Ландау, Хейльборн, Риччи), позволил получить оценку константы Шнирельмана; будучи очень большой, она постепенно была уменьшена до 67.

Отсюда до гольдбаховской тройки, конечно, очень далеко! Но важно то, что это доказано для любых чисел, сколь бы велики они ни были. Относительно какого-нибудь совершенно фантастического числа вроде

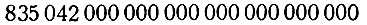
или нашего знакомца 9⁹⁹, для записи которого нужно 30 томов, тоже можно утверждать, что 67 простых слагаемых достаточно для их представления. Даже скьюзовский гигант 10¹⁰¹⁰³⁴, совершенно не поддающийся восприятию, можно, на основании доказательства Шнирельмана, представить в виде суммы не более 67 простых слагаемых (некоторые из этих слагаемых сами неизмеримо велики: гораздо больше числа 9⁹⁹). Значит, результат Шнирельмана является огромным достижением; а главное - проложены новые пути, придуманы новые способы подхода к решению старой задачи. Значит, можно ждать и новых результатов. Так оно и получилось.

В 1937 г. в учёном мире произошло событие, совершенно неожиданное для математиков. Академик Иван Матвеевич Виноградов, ныне Герой Социалистического Труда и лауреат Сталинской премии, тогда уже известный всему учёному миру своими работами по аддитивной теории чисел, почти полностью решил проблему Гольдбаха, ещё так недавно считавшуюся недоступной.

И. М. Виноградов

Результат, полученный И. М. Виноградовым, можно сформулировать так: для всех достаточно больших нечётных чисел проблема Гольдбаха решена полностью; или так: константа Шнирельмана для достаточно больших нечётных чисел не превосходит трёх.

Почему же нельзя решение И. М. Виноградова считать полным, окончательным решением проблемы Гольдбаха; откуда взялось то злополучное "почти", о котором упоминалось выше? Дело в том, что Эйлер и Гольдбах утверждали,- и это для сравнительно небольших чисел подтвердилось на опыте,- что любое чётное число является суммой двух простых. Отсюда уже, как следствие, вытекало, что любое нечётное есть сумма не более чем трёх простых. Виноградов же доказал именно последнее утверждение о нечётных числах; отсюда непосредственно следует, что для любого чётного достаточно четырёх простых слагаемых; но достаточно ли двух,- этот вопрос остаётся открытым. Кроме того, по Виноградову, утверждение Гольдбаха справедливо для всех достаточно больших нечётных чисел, иными словами, начиная с некоторого большого числа, которое некоторое время оставалось неизвестным.

В 1939 г. оно было вычислено молодым советским математиком К. Г. Бороздкиным. Это большое число может быть записано так:

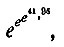
где число e есть основание натуральных логарифмов: e = 2,7182... Остаётся значительно снизить найденное К. Г. Бороздкиным число и тогда непосредственно проверить все меньшие числа,- работа, которой занимались Кантор и Обри в пределах первых двух тысяч.

Мы задержались на проблеме Гольдбаха не только потому, что она очень интересна с разных точек зрения, но и потому ещё, что ею смело может гордиться русская наука. Поставлена она была в Петербурге - нынешнем Ленинграде; первый сдвиг в её решении после почти двухсотлетнего топтания на месте сделал советский учёный - Л. Г. Шнирельман, и решил её тоже наш академик - И. М. Виноградов.