Глава XI. Эратосфеново решето

В предыдущих главах нам нередко встречались простые, или первоначальные, числа. Мы говорили уже, что простым называется число, имеющее ровно двух делителей: самого себя и единицу. Единица, имеющая только одного делителя, к простым числам не причисляется. Числа 2, 3, 5, 7, 11, очевидно,- простые. Напротив, числа 4, 6, 8, 9 - составные.

Число и наука о нем

Прежде чем ставить общие задачи, связанные с простыми числами, рассмотрим простые числа в пределах хотя бы от единицы до тысячи и постараемся путём непосредственного обзора подметить простейшие их свойства.

Как же найти все простые числа в пределах первой тысячи? Для этого поступают следующим образом: выписывают все числа от единицы до тысячи. Зачёркивают единицу (она не является простым числом). Затем подчёркивают число 2 и зачёркивают все числа, кратные двум (чётные), т. е. все числа через одно; получается таблица такого вида:

и так далее.

Далее подчёркивают первое из оставшихся незачёркнутыми чисел (3) и зачёркивают все числа "через два на третье" (т. е. кратные трём); затем подчёркивают 5 (четыре уже зачёркнуто) и зачёркивают все числа, кратные пяти ("через четыре на пятое") и так далее. Получается следующая таблица:

Таким образом, мы вычеркнем все составные числа и получим таблицу простых чисел (она приложена в конце книги на стр. 162).

Впервые такую таблицу составил греческий математик Эратосфен из Киренаики (III в. до н. э.). Он писал числа на папирусе, натянутом на рамку, и не зачёркивал, а прокалывал составные числа. Получалось нечто вроде решета, сквозь которое как бы "просеивались" все составные числа, а простые оставались. Поэтому таблицу простых чисел до сих пор зовут "эратосфеновым решетом".

Приглядываясь к эратосфенову решету, мы замечаем, что в начале таблицы простые числа расположены гораздо гуще, чем, например, вблизи тысячи. Так, в первом десятке (от 1 до 10) мы встречаем четыре простых числа: 2, 3, 5, 7. А между простыми числами 997 и 1009 имеется одиннадцать составных чисел подряд. Если зайти достаточно далеко, то можно найти какой угодно длинный числовой промежуток, т. е. сколь угодно длинный ряд натуральных чисел, состоящий сплошь из чисел составных.

Докажем, например, что существует числовой промежуток, состоящий из ста составных чисел подряд. Для этого рассмотрим число, представляющее собой произведение всех натуральных чисел от 1 до 101, т. е. число

Это - очень большое число. Оно равно приблизительно 95*10¹⁵⁸, т. е. значительно больше обычных "астрономических" чисел. (Но оно ничтожно мало рядом с числом Курта Лассвица или с числом 999, см. стр. 17-19.) Обозначим это число буквой А. Рассмотрим теперь ряд чисел:

Это - серия из ста целых чисел подряд. Каждое из них - составное. Возьмём, например, первое из них, т. е. А + 2; оно делится на 2. Действительно, А, имея по условию множителем 2, делится на 2. Само число 2 (второе слагаемое), очевидно, делится на 2. Следовательно, и сумма к разделится на 2, т. е. будет числом составным. Точно так же А + 3 разделится на 3, А + 4 - на четыре и т. д.; 1 наконец, А + 101 разделится на 101, потому что в А входит множителем 101. Таким образом, все числа найденного нами ряда -числа составные, что мы и хотели сказать.

Точно так же доказывается, что можно найти какой угодно длинный ряд (содержащий хотя бы тысячу или (миллион чисел), состоящий сплошь из составных чисел. При этом, естественно, возникает мысль: может быть, начиная с некоторого числа, все числа являются составными? Может быть, существует лишь конечное, ограниченное количество простых чисел, а всё остальное бесконечное множество чисел суть числа составные? Может быть, существует самое большое простое число? Что же это за число?

Подобные вопросы занимали уже древних математиков. Евклид, о котором говорилось в главе VI, занимался,этой задачей и дал полное её решение. Ему удалось доказать, что число простых чисел бесконечно, что не существует наибольшего простого числа. Докажем это предложение.

Мы будем, следуя Евклиду, доказывать его с помощью приёма, который называется "доказательством от противного"^*. Иными словами, допустив, что существует наибольшее простое число, мы в результате правильных рассуждений придём к нелепости. Это и покажет, что, предположение о существовании наибольшего простого числа неправильно, что такого числа нет.

^* (В настоящее время имеется много различных доказательств теоремы о бесконечности множества простых чисел.)

Итак, предположим, что существует наибольшее простое число. Обозначим его через р. Рассмотрим число, представляющее собой произведение всех простых чисел от 2 до р, т. е. число 2*3*5*7*11*...*р. Прибавим к полученному числу единицу. Получим

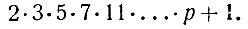
Это число, конечно, гораздо больше, чем р. Докажем, что оно не может быть составным.

Действительно, первое слагаемое, 2*3*5*...p, как произведение всех простых чисел, делится на любое простое число, а второе слагаемое (единица) при делении на любое целое число, кроме единицы, даёт в частном нуль и в остатке единицу. Значит, и сумма 2*3*5*7*...*p+1 при делении на любое простое число даст в остатке единицу (сравнима с единицей по любому простому модулю), т. е. на простое число не разделится. Но и на составное число оно делиться не может. Действительно, каждое составное число является произведением простых чисел, а если бы число 2*3*5*7*...*p+1 делилось на произведение, то оно делилось бы и на сомножителей^*, т. е. на простые числа, что, как мы видели, невозможно. Итак, число 2*3*5*7*... не делится ни на какое число (кроме, разумеется, самого себя и единицы), т. е. оно является числом простым; ранее мы видели, что оно больше р. Таким образом, предположив, что р — наибольшее простое число, мы нашли простое число ещё большее. Это противоречие убеждает нас, что исходное предположение неправильно, т. е. что наибольшего простого числа быть не может: число простых чисел бесконечно.

^* (Вспомним теорему первую главы VI (стр. 58). Мы тогда уже говорили, что она нам пригодится.)

Все простые числа, начиная с трёх, можно разбить на две категории. Одни (например, 5, 13, 17) имеют вид 4n+1; другие (например, 3, 7, 11) имеют вид 4n-1. Никакого иного вида нечётное число (а все простые числа, кроме числа 2,— нечётны) иметь не может, так как при делении нечётного числа на 4 возможны остатки, равные только 1 или 3. Разумеется, не всякое число вида 4n±1 простое, но всякое простое число имеет один из этих видов. Спрашивается: в каждом ли из этих классов содержится бесконечное множество простых чисел, или же один из них конечен, а другой — нет? Оба они быть конечными, разумеется, не могут.

Исследование показало, что и тех и других чисел бесконечно много. Для чисел вида 4n+1 доказательство б этого утверждения несколько громоздко, и мы ограничимся тем, что докажем бесконечность множества простых чисел вида 4n-1.

Докажем предварительно следующее вспомогательное предложение (лемму): «Произведение нескольких чисел вида 4n+1 само есть число вида 4n--1».

Рассмотрим два числа этого класса: 4а+1 и 4b+1. Перемножим их:

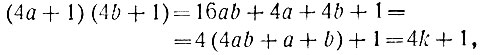
где через k обозначено целое число 4ab+a+b. Мы видим, что произведение двух множителей вида 4n+1 обязательно имеет тот же вид. Присоединяя третий, четвёртый и т. д. множители, мы убедимся, что то же самое можно сказать о произведении любого числа таких множителей.

Перейдём теперь к теореме о числах вида 4n—1 и применим к ней евклидов приём доказательства. Допустим противное — что

простых чисел вида 4n—1 — конечное количество, например m. Обозначим их р₁, р₂,..., р_m. Рассмотрим число

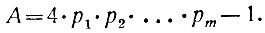
Оно должно иметь хотя бы один (простой) множитель вида 4n—1, потому что оно само имеет вид 4n—1, а произведение множителей вида 4n+1, как мы видели, должно иметь вид 4n+1. Итак, среди простых множителей числа А должно быть некоторое р = 4n-1. Но р не может равняться ни одному из чисел p₁, p₂, ..., p_m, потому что ни на одно из этих чисел наше А не делится; это р — простое число вида 4n-1. Следовательно, числами p₁, p₂, ..., p_m не исчерпываются все простые числа вида 4n — 1; а это противоречит нашему исходному предположению. Таким образом, простых чисел вида 4n — 1 бесконечно много.

Числа вида 4n—1 образуют арифметическую прогрессию с первым членом 3 и разностью 4 (÷3, 7, 11, 15, ...). Доказанную только что теорему можно было бы сформулировать и так: в бесконечной арифметической прогрессии

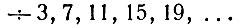
содержится бесконечное же множество простых чисел.

Спрашивается, нет ли ещё прогрессий, обладающих тем же свойством? Мы видели, что прогрессия с первым членом 1 и разностью 1 (сам натуральный ряд) содержит бесконечное количество простых чисел. То же самое говорилось (хотя мы и не доказывали этого) о прогрессии ÷ 1, 5, 9, 13, 17, 21, ..., т. е. о числах вида 4n+1.

Вопрос о количестве простых чисел в той или иной арифметической прогрессии занимал многих математиков, особенно на рубеже XVIII и XIX столетий. Решил его полностью Лежён-Дирихле (1805—1859 гг.), который доказал, что любая арифметическая прогрессия, первый член и разность которой взаимно-просты, содержит среди своих членов бесконечное множество простых чисел. Оговорка относительно взаимной простоты первого члена и разности очень существенна: если они имеют общий множитель, отличный от единицы, то, очевидно, все члены прогрессии будут содержать этот множитель и, следовательно, будут числами составными.

Изложить доказательство Дирихле элементарно — совершенно невозможно.

Упомянем, кстати, ещё об одной проблеме, которая естественно возникает при внимательном рассматривании эратосфенова решета и которая до сих пор не решена. Среди простых чисел встречаются «числа-близнецы», т. е. пары соседних нечётных чисел, являющихся одновременно простыми. Таковы, например, числа 5 и 7, числа 11 и 13, числа 17 и 19 и т. д. В начале «решета» подобные пары встречаются довольно часто, но по мере продвижения в область больших чисел, их становится, всё меньше и меньше. В первой сотне имеется 8 таких пар (3 и 5; 5 и 7; 11 и 13; 17 и 19; 29 и 31; 41 и 43; 59 и 61; 71 и 73); между числами 501 и 600 — только две пары (521 и 523; 569 и 571). Дальше они встречаются очень неравномерно, но в общем - всё реже и реже, 1 значительно реже, чем сами простые числа. Впрочем известны и весьма солидные пары «близнецов», например 5 971847 и 5 971849. Спрашивается, будет ли среди этих пар последняя? Этого до сих пор не удалось установить. Мало того, до сих пор не намечено даже пути, следуя которому можно было бы приблизиться к решению этой проблемы.

Важнейшим вопросом, связанным с простыми числами, является вопрос о возможности разложения любого числа на простые множители, т. е. о возможности представления любого числа в виде произведения простых чисел 1 и притом единственным образом. Эта возможность кажется нам совершенно очевидной, и мы в предыдущих главах неоднократно её использовали. Но в действительности предложение о разложении на простые множители является теоремой, которую нужно и можно доказать. Она настолько важна в теории чисел, что её нередко называют «основной теоремой арифметики». Вот как она формулируется: «Всякое натуральное число разлагается единственным образом на простые множители». Докажем 1: эту теорему.

Предварительно докажем вспомогательную теорему (лемму). Именно, докажем, что из делимости произведения kl на простое число р следует, что хотя бы один множитель (либо k, либо l, а может быть и оба) делится на р.

Действительно, число к либо делится на р,— и тогда теорема доказана,— либо нет. Если к не делится на р, то числа k и р взаимно-просты, потому что к, не делясь р на р, не содержит его в числе своих множителей, а р, будучи простым, никаких иных множителей, кроме единицы и самого р, не имеет. Но если к взаимно-просто с р, а произведение kl делится на р, то l должно делиться на р (теорема третья главы VI, стр. 58). Следовательно, l делится на р.

Эта лемма без труда распространяется на любое число Умножителей: если произведение аb... h делится на простое число р, то на него делится по крайней мере одно из чисел а, b,..., h.

Переходим теперь к доказательству самой теоремы — доказательству того, что всякое натуральное число разлагается единственным образом на простые множители. Здесь, собственно, не одно, а два утверждения, утверждается, во-первых, возможность разложения на простые множители, и, во-вторых, единственность такого разложения.

Что разложение возможно, это очевидно. Пусть дано некоторое число N. Если оно простое, то теорема доказана, ибо его можно считать собственным единственным простым множителем. Если же оно составное, то разделится на какое-то простое число р, меньшее чем N. В частном получится число N₁, тоже меньшее чем N. Если N₁ просто, то N = p₁N₁, и теорема доказана. Если же N₁, не является простым числом, то оно разделится на некоторое простое число р₂, меньшее чем N₁, и в частном получится N₂, тоже меньшее чем N₁. Числа N₁, N₂, N₃ и т. д. всё время уменьшаются, и число их не может быть бесконечным. Поэтому дойдём до последнего частного,— числа p_m — уже простого, и получим представление числа N в виде произведения простых чисел p₁p₂...p_m.

Это всё очень просто и почти очевидно. Существенной является вторая часть теоремы, именно утверждение, что разложение числа N на простые множители единственно. Предположим, что нам удалось двумя путями разложить число N на простые множители; первый метод дал разложение

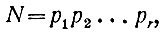
а второй — разложение

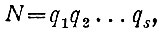
где все р и q — простые числа.

Имеем, очевидно,

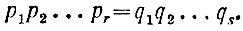
Левая часть этого равенства делится на p₁; значит, и правая, т. е. произведение q₁, q₂,... q₃, на него разделится. Но в силу леммы один из множителей q₁, q₂,..., q_s должен разделиться на p₁. Допустим, что q₁ делится на р₁ (мы всегда можем перенумеровать числа q именно таким образом). Число q₁, будучи простым, делится только на единицу и на самого себя; следовательно,

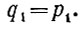
Поделив обе части равенства (*) на 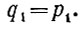получим:

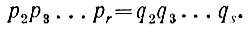
Повторив это же рассуждение, получим:

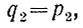
а после нового сокращения придём к соотношению:

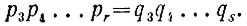
Точно так же найдём, что q₃ = р₃; q₄ = р₄;... q_s = р_s. Следовательно, множителей q столько же, сколько множителей р, каждое q равно некоторому р, т. е. оба разложения числа N на простые множители — тождественны.

Как практически разлагать числа на простые множители, читатели помнят из школьного курса. Так, например, разложение числа 8316 на простые множители выполняется следующим образом:

Любое число N можно, таким образом, представить единственным образом в форме

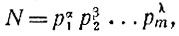
где р₁, р₂, ...,р_m — простые числа, а α, β, ..., λ — некоторые показатели. Такое представление числа N иногда (называют «каноническим разложением числа на сомножители.

Прежде чем расстаться с основной теоремой арифметики, сделаем ещё одно замечание. Мы определили простое число как такое, которое не имеет делителей, кроме самого себя и единицы. Далее, мы доказали, что если произведение нескольких чисел делится на простое число, то на него непременно разделится хотя бы один из множителей (лемма к основной теореме). Можно было бы доказать теорему, обратную этой лемме, именно - доказать, что всякое число, на которое обязательно делится хотя бы один множитель делящегося на него произведения нескольких чисел, не имеет иных множителей, кроме единицы и самого себя. Поэтому именно последнее свойство можно принять за определение простого числа. Так часто и делают: именно, простым числом называют число, на которое произведение может делиться только в том случае, если на него делится один из множителей; а число, не имеющее иных делителей, кроме себя и единицы, называют неразложимым. Пользуясь этими терминами, мы можем лемму сформулировать так: "Всякое неразложимое число - просто"; а обратную ей теорему так: "Всякое простое число-неразложимо". Обе эти теоремы можно соединить в одну: термины: "простое число" и "неразложимое число" - значат одно и то же.

Искушённый различными арифметическими сюрпризами читатель не станет спрашивать: "зачем было вводить два термина, если они обозначают одно и то же?" Читатель чувствует, конечно, что здесь скрыт какой-то подвох. Ведь если есть "арифметики", в которых трижды три - четыре и 3*3=10, то почему бы не быть и такой арифметике, в которой простые числа не являются неразложимыми, а неразложимые - простыми?..

Правда, такая арифметика кажется невероятной. Ведь именно лемма, смысл которой, по существу, и состоит в отождествлении понятий простоты и неразложимости, позволила нам доказать, что разложение любого числа на простые множители - единственно. Неужели возможны такие "арифметики", в которых одно и то же число разлагается на неразложимые множители несколькими различными путями, т. е. имеет несколько канонических разложений?

Оказывается, что возможны. Существуют такие числовые системы, в которых разложение чисел на неразложимые множители не единственно, а на простые - не всегда возможно. Именно наличие этих систем и привело к необходимости различать числа простые и числа неразложимые. Правда, те числовые системы, которые привели к установлению этих понятий, очень сложны, и говорить здесь о них, несмотря на всю их важность для высших отделов Теории Чисел, невозможно. Но мы рассмотрим простой искусственный пример, который поможет разобраться в существе дела.

Рассмотрим ряд всех чётных положительных чисел, т. е. числа

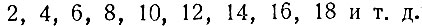
Этот ряд многими свойствами напоминает натуральный ряд. Так, например, в нём всегда выполняются обычные сложение и умножение; это значит, что сумма и произведение двух или нескольких чётных чисел дают снова число чётное. Вычитание меньшего числа из большего тоже всегда возможно. Наконец, деление с остатком (последовательное вычитание) совершенно аналогично обычному делению с остатком.

В этой числовой системе некоторые числа имеют ровно двух делителей (рассматриваются, разумеется, только чётные делители). Таковы числа 4, 6, 10, 14 и 1 многие другие, делящиеся только на два и на себя. Любое число вида 4n + 2 (где n - обычное натуральное число) будет в нашей системе иметь только два делителя. Числа такого вида и будут, с точки зрения этой системы, числами неразложимыми. Число 2, подобное единице в ряду натуральных чисел, имеет только одного делителя (самого себя). Наконец, числа 8, 12, 16, вообще числа вида 4n, имеют несколько делителей.

Пока аналогия с обычным натуральным рядом полная. Но дальше начинается расхождение. Рассмотрим число 420, принадлежащее к нашей системе (чётное). Его можно двумя путями разложить на множители, неразложимые с точки зрения нашей системы. Действительно, имеем

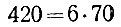
и

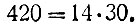
Числа 6, 14, 30 и 70 неразложимы (ни одно из них не является произведением двух чётных же чисел). Следовательно, возможно два разложения числа 420 на неразложимые далее множители.

Какие же числа будут играть в нашей системе роль простых? Нетрудно сообразить, что это будут числа вида 2p, где р - простое число в обычном смысле (сточки зрения арифметики натурального ряда). Всякое простое число будет в нашей системе неразложимым. Но не всякое неразложимое будет простым. Числа 30, 42, 70, будучи неразложимыми, не будут простыми. Лемма, предшествующая основной теореме арифметики, для них не выполняется. Поэтому-то и получилась возможность разлагать число на неразложимые дальше множители несколькими способами.

Другим парадоксом этой числовой системы будет то, что не всякое число можно будет разложить на простые множители, т. е. представить в виде произведения чисел вида 2р, где р - обычное первоначальное число. То же число 420, разложимое двумя путями на "неразложимые" множители, не может быть разложено на "простые" множители.

Чтобы закончить главу об эратосфеновом решете, скажем несколько слов о попытках найти общую формулу, которая давала бы при всех целых значениях величины n, входящей в неё, только простые числа. "Охота" за такими формулами началась ещё в классической древности и до сих пор не увенчалась успехом. Существуют различные формулы, содержащие некоторую величину n и дающие при различных целых значениях n простые числа. Но все они при некотором значении n "перестают действовать". Так, например, выражение

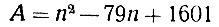
даёт простые числа при любом n, не превосходящем 79. Например, при n = 0 мы получим A = 1601, при n = 1 будет А = 1523, при n = 2 будет A = 1447, - всё числа простые. Наконец, при n = 39 получим A = 41,- тоже простое число. Далее, при значениях n от 40 до 79 получаются те же значения A, но в обратном порядке: при n = 40 будет A = 41, ... при n = 78 будет A = 1523, при n = 79 будет A = 1601. Но при n = 80 формула "отказывается служить"!

В этом случае получим:

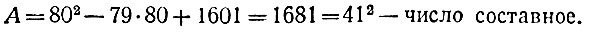
Вот ещё интересный пример^*. Если в выражение

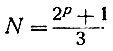
вместо р подставлять различные простые нечётные числа до 31, то значения N тоже будут простыми числами. Приводим табличку значений р и соответствующих значений N:

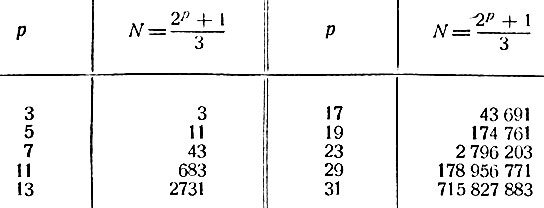
^* (Этот пример указан мне проф. А. Ф. Бермантом.)

Но формула "отказывается служить" при p = 37; при этом 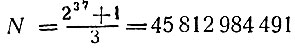- число составное; оно разлагается на 2 простых множителя, именно:

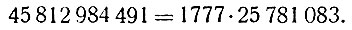
В конце предыдущей главы мы говорили о знаменитой ошибке Ферма, связанной с "охотой за формулой", дающей простые числа. Ферма считал, что при любом, целом неотрицательном n выражение 2²ⁿ+1 даёт простое число. Если математическое чутьё обмануло Ферма в том отношении, что его утверждение оказалось неправильным, то во всяком случае оно подвело его к очень важной и интересной проблеме. Оказалось, что если и не все числа вида 2²ⁿ+1 являются простыми, то те из чих, которые просты, обладают рядом замечательных свойств. Мы уже говорили, что ими занимался Эйлер, который и обнаружил ошибку Ферми. Но самый любопытный результат, относящийся к этим числам, был получен Гауссом. Он связан с известной геометрической задачей - с построением помощью циркуля и линейки правильных многоугольников.

Уже в древности умели строить правильные трёх-, четырёх- и пятиугольники. Пользуясь возможностью делить любой угол пополам, без труда строили 8-, 16-, вообще 2ⁿ-угольники; далее 6-, 12-, вообще 2ⁿ*3-угольники, 10-, 20-, вообще 2ⁿ*15-угольники. Отнимая от одной шестой части окружности одну десятую часть её, получали одну пятнадцатую: т. е. строили правильный вписанный пятнадцатиугольник, а за ним 30-, 60-, вообще 2п- 15-угольники. Но все попытки построить циркулем и линейкой правильный семи- или одиннадцатиугольник оканчивались неудачей.

Так продолжалось более двух тысяч лет. Более двух тысяч лет все попытки математиков построить циркулем и линейкой правильные многоугольники, которых не умели строить в древности, оканчивались неудачей. И только в 1796 г. девятнадцатилетний Гаусс неожиданно для всего математического мира нашёл способ построения циркулем и линейкой правильного семнадцатиугольника, а через пять лет опубликовал решение задачи о правильных многоугольниках в общем виде.

Гаусс доказал следующую замечательную теорему: циркулем и линейкой можно построить только такие правильные многоугольники (с простым числом сторон) у которых число сторон есть "простое число Ферма", т. е. число вида 2²ⁿ + 1 (при тех значениях n, разумеется, при которых эта формула даёт простое число, что, как мы знаем, осуществляется не всегда). При n = 2 получается правильный 17-угольник, при n = 3 - правильный 257-угольник. Если число сторон правильного многоугольника - простое, но не является числом Ферма, то его построение классическими средствами - циркулем и линейкой - невозможно. Правильные многоугольники с семью, с одиннадцатью, с тринадцатью сторонами построить циркулем и линейкой нельзя, а с 17 и 257 сторонами - можно!

Сам Гаусс, решив задачу в общем виде, дал разработанный до конца метод построения только для семнадцатиугольника. Следующими после 17 "числами Ферма" являются 257 и 65 537. Законченное построение многоугольника с 257 сторонами дал Ришело (оно занимает 80 страниц), а многоугольник с 65 537 сторонами построил (по гауссову же методу) Гермес (рукопись занимает довольно объёмистый ручной чемодан и хранится в Гёттингене). Теория Чисел оказалась любопытнейшим образом связанной с геометрией.

После смерти Гаусса ему поставили в Гёттингене памятник на пьедестале, имеющем форму правильной 17-угольной призмы.