Глава X. Ещё о делимости; "большая" теорема, которую зовут "малой"

Разбирая на стр. 87 задачу о пифагоровых треугольниках, мы были вынуждены использовать предложения, подобные следующему: "сумма или разность двух чётных или двух нечётных чисел представляют собой числа чётные". Эти предложения, несомненно, относятся к учению о делимости; но в отличие от признаков делимости, разобранных в предыдущей главе и существенно связанных с выбором системы счисления, здесь выбор системы счисления не играет никакой роли.

Число и наука о нем

В качестве первого примера рассмотрим разность между квадратом нечётного числа и единицей, т. е. выражение m² - 1, где m - число нечётное. Нетрудно убедиться, что при любом (нечётном) m эта разность должна разделиться на 8. Действительно, она разлагается на множители:

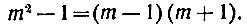
Раз m - число нечётное, значит оба множителя в правой части будут чётными, причём, очевидно, соседними чётными числами, потому что разность между ними равна m + 1 - (m - 1) = 2. Но из двух соседних чётных чисел одно обязательно делится на 4^*. Значит, один из множителей делится на 4, да ещё второй введёт двойку. Всё произведение будет делиться на 2*4=8.

^* (Действительно, если одно из них, будучи чётным, не делится на 4, то при делении на 4 оно может давать в остатке только 2, т. е. иметь вид 4n + 2. Но чётными соседями этого числа будут числа (4n + 2) ± 2, т. е. 4n и 4n+4; оба они кратны четырём.)

Можно рассуждать и иначе: раз m по условию нечётное число, значит, его можно записать в виде 2k + 1, где k - произвольное число (натуральное или нуль). Получим:

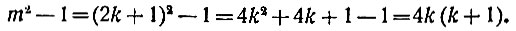
Из двух соседних чисел k и k +1 одно обязательно чётное. Значит, в состав нашего выражения, кроме коэффициента 4, войдёт ещё множитель, равный двум, т. е. в составе его будет множитель, равный 4*2 = 8, что мы и хотели доказать.

Давая в выражении m² - 1 числу m различные натуральные значения, получим следующие числа, кратные восьми:

Пусть читатель сам докажет, что при m чётном разность m² - 1 делится на 3.

В качестве второго примера рассмотрим разность между кубом любого числа и самим числом. Эта разность, как нетрудно показать, делится на 6. Действительно, возьмём произвольное число m. Разность между кубом и самим числом равна m³ - m. Разлагая на множители, получим:

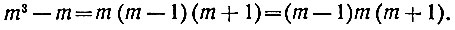
Иными словами, разность между кубом натурального числа и самим числом всегда представляет собой произведение трёх стоящих подряд натуральных чисел. Из трёх же стоящих подряд натуральных чисел по крайней мере одно - чётное (делится на 2) и одно делится на 3^*.

^* (Действительно, рассмотрим три числа, стоящие подряд: k, k+1, k+2. Первое имеет вид либо k = 3n, либо k = 3n+1, либо k = 3n+2, потому что при делении на 3 возможны только такие остатки: 0, 1, 2. Если k = 3n, то вопрос ясен. Если k = 3n+1, кто k + 2 = 3n + 3 делится на 3. Если, наконец, k = 3n+2, то k + 1 = 3n + 3 тоже делится на 3. Во всех возможных случаях одно из трёх стоящих подряд чисел оказывается кратным числа 3.)

Следовательно, разность между кубом натурального числа и самим числом делится на 2*3 = 6, что мы и хотели доказать.

В качестве третьего примера рассмотрим задачу, обошедшую все школьные олимпиады и конкурсы: "доказать, что выражение m⁵ - 5m³ + 4m при любом натуральном m делится на 120". Для m = 1 и m = 2 это очевидно, потому что при m = 1 или 2 наш трёхчлен равняется нулю, а нуль принято считать кратным любого числа, стало быть, и ста двадцати; поэтому будем считать, что m>2.

Сделаем следующие очевидные преобразования:

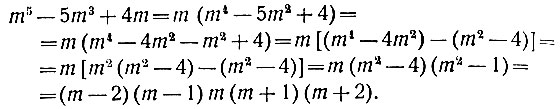
При любом m наш трёхчлен разлагается на пять множителей, представляющих собой (при m, большем двух) пять последовательных натуральных чисел. В последовательности пяти натуральных чисел найдётся по меньшей мере два соседних чётных; значит, трёхчлен будет делиться на 8. Далее, в последовательности пяти чисел имеется по крайней мере одно, делящееся на 3 (уже три первых множителя, как мы видели, обеспечивают делимость на 3). Наконец, соображениями, совершенно аналогичными тем, которые сделаны в примечании к предыдущему примеру, убеждаемся, что произведение пяти стоящих подряд натуральных чисел должно делиться на 5. Итак, наш трёхчлен делится на взаимно-простые числа 8, 3 и 5; он разделится и на их произведение, т. е. на 120. Вот несколько различных значений m и соответствующих значений трёхчлена:

Разобранные примеры, несмотря на некоторую искусственность, очень поучительны. Они подводят нас к двум любопытным теоремам. Прежде всего, мы видим, что разность m³ - m делится на 3. Так же можно доказать, что m⁵ - m делится на 5, хотя доказательство несколько громоздко. Непосредственно очевидно, что m² - m делится на 2. Напротив, m⁴ - m может при некоторых m и не делиться на 4: именно, при m = 2 мы получим m⁴ - m = 16 - 2 = 14, т. е. число, на 4 не делящееся. Возникает вопрос: при каких же именно значениях а разность m^а - m делится на показатель а при любом m, а при каких - нет. Эту задачу решил уже знакомый нам Ферма. Ей будет посвящен конец настоящей главы.

Вторая теорема, к которой подводят наши примеры, состоит в следующем. Мы видели, что произведение трёх последовательных натуральных чисел делится не только на 3 (это понятно), но и на 6, т. е. на произведение 1-2-3. Точно так же произведение пяти последовательных натуральных чисел делится не только на 5, но и на 120, т. е. на произведение 1*2*3*4*5. Читатель без всякого труда докажет, что произведение четырёх последовательных натуральных чисел делится на 1*2*3*4 = 24. Оказывается, имеет место следующая общая теорема:

Произведение m последовательных натуральных чисел

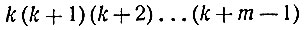
делится без остатка на произведение m первых последовательных натуральных чисел, т. е. на

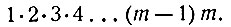
Элементарное арифметическое доказательство этой теоремы довольно громоздко; поэтому говорить о нём мы не будем. Для читателей, знакомых с теорией соединений и биномом Ньютона, заметим, что частное 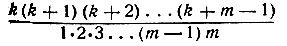сочетаний из (k + m -1) элементов по m или же коэффициенту при (m + 1)-ом члене разложения бинома (а + b)^k+m-l. Следовательно, это частное должно быть целым числом, т. е. k(k+1)...(k+m-1) должно делиться без остатка на 1*2*3...(m - 1)m.

В разобранных выше примерах разыскивались конкретные делители некоторых выражений при каком угодно (целом) значении величины n, входящей в эти выражения Часто вопрос ставится иначе: даётся некоторое выражение и требуется выяснить, может ли оно вообще при произвольном n иметь делители (отличные, разумеется от него самого и от единицы) или же всегда является числом простым. Такого рода выражения изучались в надежде найти признаки, позволяющие по виду числа по его строению решить вопрос: простое оно или нет. Примером подобного исследования может служить совсем простая теорема, найденная француженкой Софи Жермен:

"Всякое число вида n⁴ + 4, где n>1, является составным".

Докажем эту теорему. Имеем:

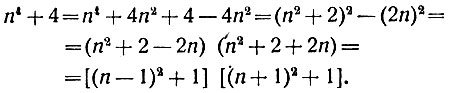
При целом n оба множителя -целые числа. При n>1 ни один из них не равен 1 и, следовательно, n⁴ + 4 является числом составным. При n=1 мы имеем исключительный случай: n⁴ + 4= 1⁴ + 4 = 5 - число простое.

Простые числа занимают математиков буквально тысячелетия. Древние греки интересовались ими две с половиной тысячи лет тому назад. Многие пытались найти признаки, позволяющие по строению числа установить - простое оно или составное. Достичь некоторого успеха на этом пути удалось впервые Ферма. В 1640 г. ему удалось доказать теорему, которая так поразила и обрадовала его, что он написал по поводу её открытия (в письме к Френиклю): "Меня озарило ярким светом".

В чём же состоит эта теорема Ферма?

Мы уже видели, что при любом m двучлен m³ - m делится на 3, двучлен m⁵ - m делится на 5. Ферма показал, что при любом простом р двучлен m^р - m делится на р, каково бы ни было число m. Этот скромный с виду результат привёл к важным обобщениям и породил довольно значительную литературу; его считают одной из основных теорем теории чисел. И всё же эту теорему называют "малой", в отличие, от "Великой теоремы Ферма", о которой было рассказано в конце главы VII.

Сам Ферма формулировал свою теорему не совсем так, как это было сделано выше. Выражение m^р - m можно преобразовать, взяв m за скобку; получится m(m^p-1 - 1). Если m кратно р, то теорема очевидна. Важен и интересен только тот случай, когда m не делится на р, Но в таком случае тир взаимно-просты, потому что только те числа могут иметь общие множители с простым числом р, которые ему кратны. В случае взаимно-простых тир должна делиться на р разность m^p-1 - 1. Так и была сформулирована теорема самим ферма: "Если р просто, а m не делится на р, то m^p-1 - 1 делится на р".

Эту же мысль можно выразить на языке сравнений. Раз m^p-1 - 1 делится на р, значит, m^p-1 и 1 сравнимы по модулю р, что, как мы знаем, записывается так:

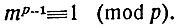
В этой форме теорема Ферма даётся в современных курсах теории чисел.

Разберём несколько примеров. Положим m = 2; тогда в качестве р можно будет взять любое простое нечётное число, т. е. любое простое, за исключением самого числа 2. В следующей таблице даны значения р, 2^р-1, 2^p-1 - 1 и показано, что 2^р-1-1 всегда содержит множителем р.

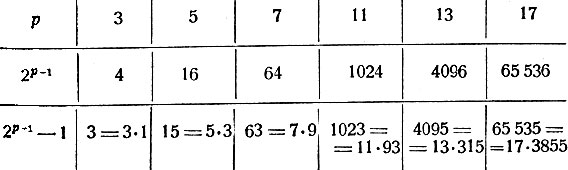
Если р не является простым числом (например, р = 15 = 3*5), то число 2^p-1- 1 не будет обязательно обладать этим свойством. Действительно, 2^13-1 - 1 = 2¹⁴ - 1 = 16 384 - 1 = 16 383 не делится на 15. Точно так же n не должно Делиться на р. Если при п=2 мы возьмём в качестве р тоже 2, то у нас ничего не выйдет: 2^2-1 - 1 = 1 Не делится на 2.

Вот ещё примеры:

Мы видим, что n не обязано быть простым (например, в третьем столбце n = 10 = 2*5).. Но оно не должно делиться на р. Поэтому при n=3 не рассматривается значение р=3, при n = 5 - значение р = 5, при n = 10 - значения р=2 и р=5. Читатель сам убедится путём подсчёта, что в этих случаях утверждение теоремы не выполняется.

Переходим к доказательству теоремы Ферма. Начнём с того, что рассмотрим полную систему наименьших положительных вычетов числа р, т. е. все остатки, которые могут получиться при делении различных чисел на р (кроме остатка, равного нулю). Вот эти вычеты:

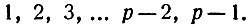(1)

Помножим каждый из них на число m, не делящееся на р. Получим

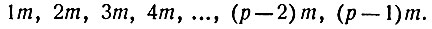(2)

Все эти числа различны, ни одно из них не равно нулю. Но этого мало: все они дают при делении на р разные остатки. Действительно, если am и bm, где а и b - различные числа из ряда (1), т. е. меньшие р, дают при делении на р одинаковые остатки, то разность am - bm = m(а - b) должна делиться на р. Число m взаимно-просто с р. Следовательно, а - b должно делиться на р. А это невозможно, потому что разность а - b не равна нулю заведомо меньше р (и а и b - положительные числа, меньшие р). Полученное противоречие показывает, что исходное предположение о возможности одинаковых остатков при делении чисел ряда (2) на р - неверно. Следовательно, все эти остатки различны, и так как их ровно р- 1, то они равны числам ряда (1), т. е. 1, 2, 3, ..., р-1, только взятым в каком-то другом порядке. Но это значит, что каждое число ряда (2) сравнимо по модулю р (равноостаточно) с одним, и только одним, из чисел ряда (1). Обозначим число из ряда (2), сравнимое с 1, через k₁, число, сравнимое с 2, - через k₂ и т. д., число, сравнимое с р-1, - через k_p-1. Получим следующий ряд сравнений:

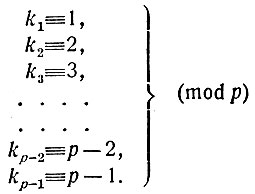
Перемножим теперь все эти сравнения, что, как мы знаем, делать можно. Получим:

(*)

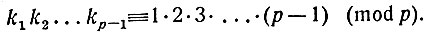Переходим к центральному пункту доказательства. Числа k₁, k₂,... , k_p-1 представляют собой все числа ряда (2), только взятые в другом порядке. Произведение их не зависит от порядка множителей; поэтому

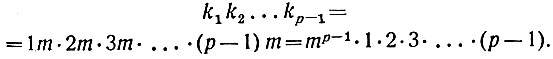
Заменяя произведение в левой части сравнения (*) равной ему величиной, получим:

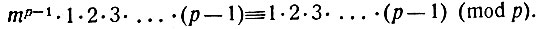
Все члены произведения 1*2*...*(p-1) меньше первоначального числа р, а потому взаимно-просты с ним. Значит, сравнение можно на них сократить.

Получится:

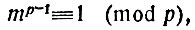
что и требовалось доказать.

Это доказательство можно изложить, не используя понятия сравнения, что и было сделано самим Ферма, жившим без малого за 200 лет до Гаусса - изобретателя теории сравнений. Такое доказательство очень громоздко. Существует любопытное доказательство теоремы Ферма, связанное с превращением простой дроби в периодическую десятичную. Но оно, во-первых, длинно, а, во-вторых, не совсем подходит к теме этой книжки, посвященной целым числам^*.

^* (Изложено оно в книге Радемахера и Теплица "Числа и фигуры", которая вообще очень интересна.)

Для читателей, знакомых с биномом Ньютона, можно привести ещё одно доказательство теоремы Ферми.

Напишем по формуле Ньютона разложение двучлена (m+1)^р, где m - целое, а р - простое число:

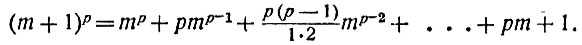
Все коэффициенты бинома Ньютона, т. е. числа вида 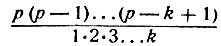- числа целые. Мало того, все они, кроме первого и последнего, делятся на р. Действительно, мы уже знаем, что в дроби 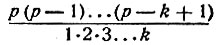числа, стоящие в знаменателе, должны полностью сократиться с множителями числителя. Но р взаимно-просто со всеми числами 1, 2, 3, ..., k. Значит, числа эти должны полностью сократиться с множителями произведения (p-1) (р - 2), ..., (р-k+1), а множитель р останется нетронутым. Итак,

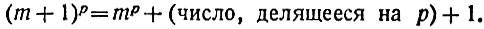
Это равенство показывает нам следующее. Если при каком-нибудь значении m двучлен m^p - m делится на р, то на р обязательно разделится и (m+1)^р-(m+1), т. е. такой же двучлен, но с основанием, на единицу большим (потому что из делимости вычитаемого и разности на некоторое число следует делимость на это число и уменьшаемого). Если m = 1, то m^р - m = 1 - 1 = 0 наверное делится на p (нуль делится без остатка на любое число). Значит, и (m+1)^р - (m+1), т. е. 2^p-2, будет делиться на р, а отсюда, в свою очередь, будет следовать, что 3^p - 3 делится на р и т. д. до произвольного значения m^*. Следовательно, m^р-m при любом m и простом р делится на р ("малая" теорема Ферма).

^* (Напомним, что подобное рассуждение называется полной к математической индукцией.)

Эта теорема была открыта Ферма в связи со следующей задачей: он искал такие выражения, содержащие букву n, которые были бы простыми числами. В связи с этим Ферма формулировал любопытную "теорему", которая оказалась неверной (см. стр. 92). Вот эта "теорема". Ферми рассматривал числа вида 2²ⁿ + 1, где n - произвольное целое число. Вот какие числа он получил, полагая n равным 0, 1, 2, 3, 4:

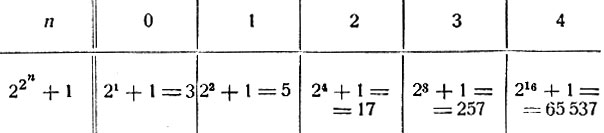
Все числа в нижней строке этой таблички (3, 5, 17, 257, 65 537) - числа простые. Ферма утверждал, что и при больших значениях n получатся простые числа. При n = 5 Ферма получил число 4294 967 297, которое он, Ферма, не сумел разложить на множители и думал, что оно тоже простое. Однако Эйлер, о котором речь будет дальше, убедился, что 4 294 967 297 делится на 641, т. е. не является простым числом. Таким образом, в Эйлер показал, что Ферма ошибся^*.

^* (Легко разделить 4 294 967 297 на 641, когда заранее знаешь, что делить нужно именно на 641. Но делить десятизначное число на все простые числа подряд (а простых чисел уже в пределах первой сотни - двадцать пять штук), не имея при этом ни достаточно больших таблиц простых чисел, ни иных вспомогательных средств,- очень трудная работа.)

Это неверное предложение очень поучительно. Своеобразное "чутьё" подсказывает талантливым математикам, в каком направлении вести исследование. Мы увидим в следующей главе, что числа Ферма, т. е. простые числа вида 2²ⁿ + 1, оказались весьма замечательными, и изучение их привело впоследствии к крупным открытиям. Далее математик работает подобно любому учёному-естественнику: он делает предположения (гипотезы), проверяет их путём наблюдения и своеобразного математического опыта, ищет аналогии и т. п. Но, получив результат путём догадки или опыта, математик обязан строго доказать его. В противном случае всегда остаётся опасение, что высказанное утверждение может оказаться ошибочным.