Глава IX. Разделится или нет?

От тел и колец, т. е. от вопросов, принадлежащих скорее алгебре, вернёмся снова к арифметике: займёмся признаками делимости. Признаки делимости на 2, 3, 4, 5, 6, 8, 9, 10, 25 всем известны. Заметим только, что в различных системах счисления признаки делимости выглядят по-разному. Вот, например, признак делимости на два: "на два делятся все числа, последняя цифра которых четна". Предположим, что мы пользуемся троичной системой счисления; в ней число "десять" записывается так: 101, т. е. оканчивается нечётной цифрой - единицей; тем не менее и в троичной, и в любой другой системе счисления число "десять" будет делиться на 2, потому что делимость на два есть внутреннее свойство числа десять, совершенно не зависящее оттого, как это число записывать. Следовательно, признак делимости, имеющий место в десятичной системе, в другой системе счисления может оказаться неверным. Есть, разумеется, и такие предложения о делимости, которые справедливы в любой системе счисления, хотя бы, например, такая теорема: "Разность между кубом любого нечётного числа и самим числом делится на шесть"; ими мы займёмся в следующей главе.

Число и наука о нем

Остановимся сначала на хорошо знакомых вещах: рассмотрим признак делимости на 9. Он поможет нам лучше понять те методы, которыми пользуются при выводе всевозможных иных признаков делимости.

Признак делимости на 9 основывается на том, что всякое число, имеющее в нашей системе счисления вид единицы с нулями (всякая степень десяти), даёт при делении на 9 остаток 1. Действительно,

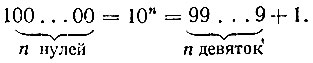
Первое слагаемое, составленное сплошь из девяток, очевидно, делится на 9. Поэтому в остатке от деления 10" на 9 будет обязательно единица.

Рассмотрим, далее, какое-нибудь произвольное число, например, 4351. Каждая тысяча даёт при делении на 9 остаток единицу. Значит, четыре тысячи дадут остаток 4. Точно так же три сотни при делении на 9 дадут остаток 3, пять десятков - 5, да ещё останется 1 (число единиц в данном числе). Следовательно,

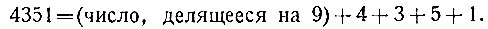
Если бы "хвост" 4 + 3 + 5 + 1, представляющий собой ("сумму цифр" данного числа, делился на 9, то и всё число разделилось бы на 9. Отсюда вывод: если "сумма цифр" данного числа делится на 9, то и само число разделится.

Слова "сумма цифр" мы взяли в кавычки, потому что, строго говоря, складывать цифры нельзя: ведь цифра - это значок, с помощью которого записывается число. Складываются, разумеется, числа, изображаемые отдельными цифрами данного многозначного числа; но для краткости условились говорить "сумма цифр".

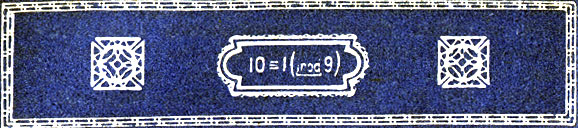
Повторим то же рассуждение, пользуясь понятием сравнения. 10 при делении на 9 даёт в остатке 1, т. е. 10 и 1 сравнимы по модулю 9:

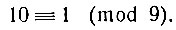
Возводим обе части сравнения в произвольную степень m; получим:

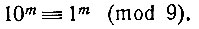
Умножив обе части этого сравнения на любое число N, получим:

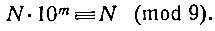
Полученный результат можно сформулировать так: произведение любого числа N на степень десяти даёт при Делении на 9 тот же остаток, что и само число N.

Рассмотрим теперь число, составленное из цифр а, b, ..., k, l, т. е. число

Это-не произведение чисел а, b и т. д., а число, содержащее l единиц, Десятков и т. д. Его можно записать и так:

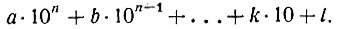
Напишем столбиком ряд сравнений, справедливых на основании только что сказанного:

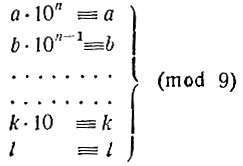
Сложим почленно эти сравнения. Слева мы получим

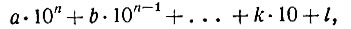
т. е. данное нам число, а справа -сумму его цифр. Следовательно, любое число и сумма его цифр сравнимы по модулю 9, т. е. либо одновременно делятся на 9, либо нет.

Признак делимости на 9 используется в следующем поучительном фокусе. Предложите товарищу написать незаметно для вас любое трёх- или четырёхзначное число, состоящее из различных цифр. Пусть он переставит цифры в каком хочет ином порядке; тогда он получит новое число. Меньшее из этих двух чисел пусть он вычтет из большего. Теперь предложите ему зачеркнуть одну цифру полученной разности и назвать вам сумму незачёркнутых цифр. Вы сейчас же сможете назвать зачёркнутую цифру.

В самом деле: и первоначальное, и "перевёрнутое" числа имеют одну и ту же сумму цифр; иными словами, они при делении на 9 дают одинаковые остатки, и, следовательно, их разность делится на 9. Но если эта разность делится на 9, то значит, на 9, в свою очередь, делится её сумма цифр. Вам сказана сумма всех цифр, за исключением одной. Следовательно, зачёркнутая цифра должна дополнять названную вашим товарищем сумму до ближайшего кратного девяти. Если, например, было написано число 2365, а после перестановки получилось 3652, то их разность будет 1287; разность эта, а значит, и сумма её цифр 1 + 2 + 8 + 7 = 18 делятся на 9. Если зачёркнута цифра 2, то останутся цифры, дающие в сумме 1 + 8 + 7 = 16. Услышав от товарища, что получилось 16, вы дополняете это число до ближайшего большего, кратного 9, т. е. до 18 (из кратных девяти: 1*9 = 9; 299=18; 3*9 = 27 и т. д.; ближайшим, большим шестнадцати будет 18). Полечите, очевидно, 18 - 16 = 2, т. е. как раз зачёркнутую цифру. Если сумма незачёркнутых цифр сама окажется кратной девяти, то, очевидно, и зачёркнутая цифра должна быть кратной девяти, т. е. равняться или 9, или 0. В этом случае вам так и придётся сказать: "зачёркнуто либо девять, либо нуль".

Займёмся теперь признаком делимости на 11. Он основан на тех же соображениях, что и признак делимости на 9. Как 10; 100; 1000 и т. д. (т. е. единица ре любым числом нулей) при делении на 9 дают в остатке единицу точно так же 100; 10000; 1000 000 (вообще - 1 единица, с чётным числом нулей) при делении на 11 дают в остатке единицу^*. Иными словами,

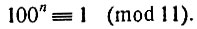
^* (Предлагаем читателю доказать это.)

Рассмотрим теперь какое-нибудь число, например, 57 385. Разобьём его на грани по две цифры в каждой, справо налево, как это делается при извлечении квадратного корня. При этом в крайней левой грани может получиться и одна цифра (что как раз имеет место в нашем примере: 5'73'85). Что представляет собой первая грань? Пять десятков тысяч (5×10000). Каждый десяток тысяч даст при делении на 11 остаток 1, значит, пять десятков тысяч дадут при делении на 11 остаток 5. Следующая грань (73) представляет собой 73 сотни. Каждая сотня даст при делении на 11 остаток 1. Значит, 73 сотни дадут в остатке 73. Остаётся ещё крайняя правая грань: 85. Значит, наше число равно

т. е. числу, делящемуся на 11 + "сумма граней". Отсюда получается следующее правило:

Если сумма граней делится на 11, то и всё число разделится на 11.

В нашем примере сумма граней равна 5 + 73 + 85 = 163. Полученный результат не делится на 11; значит, и 57 385 не разделится на 11. Если при сложении граней получится большое число, то его, в свою очередь, можно разбить на грани и испытать их сумму; в нашем примере имеем: 163 = 1'63. Складываем грани; 1 + 63 = 64 - не делится на 11; значит, и исходное число не делится на 11.

Ещё пример:

563 035 делится на 11. Действительно, разбиение на грани даёт 56'30'35 (здесь первая грань состоит из двух цифр). Складываем грани 56 + 30 + 35 = 121. Сумма граней делится на 11; значит, и 563 035 делится на 11.

Не следует думать, что для каждого числа существует единственный признак делимости. Вот ещё признак делимости на 11. Сложим отдельно все цифры данного числа, стоящие на чётных местах, и все цифры, стоящие на нечётных, и из большего итога вычтем меньший^*. Если разность делится на 11 (или равна нулю; нуль делится на любое число), то и данное число разделится на 11.

^* (Понятно, что в этом случае безразлично, считать ли цифры справа налево или слева направо: если число цифр в числе нечётное, то каждая цифра будет одинаковой чётности и слева и справа, а если число цифр чётное, то при счёте слева и справа чётность цифр изменится, но сумма чётных цифр останется равной или неравной сумме нечётных цифр.)

Рассмотрим пример. Пусть дано число 8 230 541. На нечётных местах (считая справа) стоят цифры: 1 (на первом месте), 5 (на третьем), 3 (на пятом), 8 (на седьмом); складывая эти цифры, получим 1 + 5 + 3 + 8 = 17. На чётных местах стоят цифры: 4 (на втором), 0 (на четвёртом), 2 (на шестом); их сумма равна 4 + 0 + 2 = 6. Разность 17 - 6 = 11 делится на 11. Значит, и число 8230541 разделится.

Пусть читатель подумает сам, как доказать этот признак делимости. Рассуждение будет особенно просто, если использовать понятие сравнения.

Рассмотрим задачу, связанную с признаками делимости на одиннадцать.

Задача. Написать наименьшее делящееся на 11 шестизначное число, первая цифра которого 7 и все цифры различны.

Пишем вслед за семёркой четыре цифры, начиная с нуля, в порядке их роста: 70123. Ясно, что таким образом мы получим наименьшее число нужного нам вида. Остаётся приписать последнюю цифру так, чтобы всё число разделилось на 11.

Сумма цифр, стоящих на нечётных местах (считая слева), равна 7+1+3 = 11; сумма цифр, стоящих на чётных местах, равна 2. Чтобы разность сумм цифр, стоящих на чётных и нечётных местах, делилась на 11 или равнялась нулю, последняя цифра должна быть девяткой (7+1+3 = 0 + 2 + 9). Значит, искомое число - 701239.

Совершенно аналогичен признак делимости на 37. Число 1000 и все его степени (т. е. числа, изображаемые единицей с числом нулей, кратным трём) дают при делении на 37 остаток, равный 1. Действительно, 999 делится на 37 (получается 27). Значит,

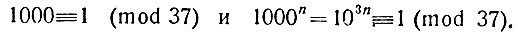
Если при испытании делимости на 11 мы разбивали число на грани по две цифры в каждой, то при испытании делимости на 37 приходится делить его на грани по три цифры в каждой, тоже справа налево. При этом в крайней левой грани могут получиться одна, две или три цифры. Если сумма граней делится на 37, то и всё число разделится. Например, 25 012 делится на 37: разбивая на грани, получим 25'012; сумма граней равна 25+12 = 37.

Переходим к признакам делимости на 7 и на 13. Они основаны на том, что 1001 делится на 7 и на 13; кстати, 1001 делится и на 11, так что мы, мимоходом, получим третий признак делимости на 11.

Рассмотрим какое-нибудь число, например 357 285. Это число содержит 357 тысяч и 285 простых единиц. Его можно записать так: 357000+285. Прибавим и отнимем от нашего числа число его тысяч, т. е. 357; от этого ничего не изменится; сделаем далее простые преобразования:

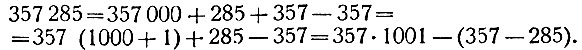
Первое слагаемое, очевидно, делится на 1001; значит, судьба нашего числа зависит от выражения в скобках; но в скобках стоит разность между числом тысяч данного числа и числом его простых единиц^*. Если эта разность делится на 7, 11 или 13, то и само число разделится. Заметим, что число тысяч может оказаться меньше числа простых единиц; тогда, разумеется, из большего вычитаем меньшее.

^* (Имеются в виду не разряды, а классы тысяч и простых единиц.)

Рассмотрим число 208 824 525. В нём 208 824 тысячи и 525 простых единиц. Вычитаем из числа тысяч число единиц: 208824 - 525 = 208299. Нужно узнать, делится ли на 7, 11 или 13 это число. Повторяем наш приём. Теперь число единиц (299) больше числа тысяч (208). Вычитаем из большего меньшее: 299-208 = 91. Полученное число (91) делится на 7 и на 13, но не делится на 11. Значит, и 208824 525 делится на 7 и на 13, но не делится на 11.

Со свойствами числа 1001 связан любопытный арифметический фокус. Предложите кому-нибудь написать какое угодно трёхзначное число так, чтобы вы не видели, какое. Предложите, далее, приписать к этому числу справа такое же число (если, например, было задумано 167, то получится 167 167). Предложите разделить результат на 7. Всё благополучно разделится, хотя, казалось бы, взятое наугад число вовсе не обязано делиться на 7. Результат предложите разделить на 11; снова всё благополучно разделится! Наконец, последний результат предложите разделить на 13. Деление пройдёт без остатка, и в результате получится первоначально задуманное число.

Секрет фокуса очень прост. Приписав справа от задуманного числа его самого, мы тем самым умножаем его на 1001 (если, например, задумано число 167, то будем иметь 167 167 = 167000 + 167 = 167 (1000+1) = 167*1001. Но 1001 = 7*11*13. Значит, разделив 167 167 последовательно на 7, 11 и 13, мы разделим его на 1001. Сперва мы умножили задуманное число на 1001, а потом разделили. Понятно, что все деления прошли благополучно, . и в итоге получилось само задуманное число.

Мы говорили уже, что в разных системах счисления признаки делимости на одно и то же число - различны. Так, например, в системе счисления с основанием 3 число, оканчивающееся нечётной цифрой, может делиться на 2. Установим признак делимости на 2 в троичной системе счисления. Число 3 при делении на 2 даёт остаток 1. То же можно сказать о любой степени трёх, " потому что всякая степень трёх, не содержа множителем двойку, при делении на 2 даёт в остатке единицу. Повторив те же рассуждения, которыми мы пользовались при выводе обычного признака делимости на 9, убедимся, что в троичной системе счисления на 2 делятся такие, и только такие, числа, сумма цифр которых делится на 2. Число 10201^*, например, сумма цифр которого равна четырём, должно делиться на 2. Действительно, число 10201 равно 1*3⁴ + 0*3³ + 2*3² + 0*3 + 1 = 81 + 18 + 1 = 100, а сто, очевидно, на 2 делится.

^* (Жирный шрифт, как и в главах IV и V, обозначает число, записаннное в недесятичной, в данном случае в троичной системе счисления.)

Найдём все системы счисления, в которых признаком делимости любого числа на данное число а является делимость его суммы цифр на число а.

Заметим прежде всего, что этот признак делимости можно сформулировать иначе, именно так: разность между любым числом и суммой его цифр должна делиться на а. Действительно, в этом (и только в этом!) случае из делимости любого числа на а будет следовать делимость на а суммы его цифр и наоборот.

Обозначим основание искомой системы счисления буквой n. Число n, как основание системы счисления, запишется так: 10; его сумма цифр равна единице. Значит, n-1, разность между числом и его суммой цифр, должна делиться на а, что запишется следующим образом: n-1 = mа, где m - любое натуральное число (или нуль). Отсюда следует, что искомое основание n системы счисления должно равняться увеличенному на единицу кратному числа а:

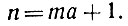
Обратно: из этого равенства следует, что любая степень n при делении на а даст в остатке единицу. В самом деле, наше равенство выражает совершенно то же, что сравнение

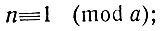
возведя это сравнение в любую степень k, получим:

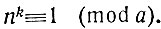
Но если любая степень основания системы счисления даёт при делении на А в остатке единицу, то, повторив слово в слово вывод обычного признака делимости на 3 или на 9, убедимся, что делимость суммы цифр некоторого числа на а обеспечит делимость на а самого этого числа.

Итак, наш признак делимости будет иметь место во всех системах счисления, основание которых на единицу больше произвольного кратного числа а. Например, делимость суммы цифр будет обеспечивать деление числа на 9 не только в десятичной (10 = 1*9+1), но и в девятнадцатиричной (19 = 2*9+1), и в двадцативосьмиричной (28 = 3*9+1), и во всех системах с основанием, равным 9m+1. Ни в каких иных системах счисления этот признак делимости не будет иметь места.

Вот ещё задача: найти наименьшее основание системы счисления, в которой имеют место следующие признаки делимости:

1°. Если сумма цифр некоторого числа делится на 5, то и само число разделится на 5.

2°. Если число, образованное двумя последними цифрами произвольного числа, делится на 7, то и само число разделится на 7.

Из предыдущей задачи мы знаем, что первому условию можно удовлетворить, взяв в качестве основания системы счисления число вида 5m+1:

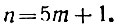
Займёмся вторым условием. Если делимость некоторого числа на 7 обусловливается делимостью на 7 числа, образованного его двумя последними цифрами, то, значит, единица третьего разряда 100 = n² должна делиться на 7^*; тогда и любое число единиц третьего разряда будет делиться на 7, и вопрос сведётся к исследованию второго и первого разрядов. Итак, n² должно делиться на семь: n² = 7p. Чтобы правая часть равенства была точным квадратом, число р должно равняться 7, умноженному на точный квадрат: р = 7k²; мы будем иметь

^* (Так, в десятичной системе счисления, признак делимости на 4 или на 25 заключается в делимости на эти числа нашей единицы третьего разряда - сотни.)

Для определения n получилось два линейных уравнения с тремя неизвестными:

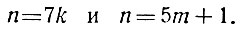
Приравнивая друг другу правые части, получим одно неопределённое линейное уравнение с двумя неизвестными:

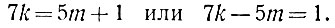
Решать такие уравнения в целых числах мы умеем. Без особого труда найдём:

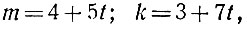
где t - любое целое число; следовательно, n = 21 + 49t. Наименьшее положительное значение n = 21 получится при t=0.

Число 21 и будет ответом на нашу задачу. Наименьшим основанием системы счисления, в которой имеют место данные выше признаки делимости, является число 21.

Разобрав вопрос о связи признаков делимости с различными системами счисления, мы перейдём к таким теоремам о делимости чисел, которые от системы счисления не зависят.