Глава VIII. Арифметика, в которой "трижды три-четыре"

Мы уже рассматривали (на стр. 43) арифметику, в которой 3×3 = 10. Это - система счисления при основании 9. Разумеется, и в этой, и во всякой другой системе счисления три раза повторенное число три будет равно девяти; но в десятиричной системе счисления само число девять, будучи единицей второго разряда, выглядит так: 10. Поэтому и получилась парадоксальная запись.

Число и наука о нем

Теперь мы собираемся говорить не о способе записи. Мы покажем, что существует такая точка зрения, вполне разумная и в некоторых случаях полезная, при которой три, умноженное на три, даёт четыре. Чтобы понять возможность такой точки зрения, вернёмся на время к линейным неопределённым уравнениям, которые рассматривались нами в предыдущей главе.

Рассмотрим уравнение

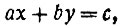
где а, b, с - целые числа, причём а и b - взаимно-простые. По существу, при решении важно найти только х. Тогда y определится сразу:

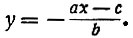
При этом х нужно искать с таким расчётом, чтобы выражение, которому равен y, было целым. Но это выражение наверное будет целым, если ах-с разделится на b или, иначе, если ах при делении на b даёт остаток с. (Действительно, если ах при делении на b даёт остаток с, то это значит, что ах = bm + с, отняв отсюда с, получим bm, очевидно, делящееся на b.)

В этой задаче нахождение y, когда х уже найдено, не представляет никакой трудности, и мы можем y вообще не рассматривать. А задачу - найти х - можно поставить так, что в ней y совсем не будет участвовать. По существу, здесь поставлена следующая задача: найти такое х, чтобы произведение ах при делении на b давало остаток с.

Для начала предположим, что a = 1. Это, очевидно, простейший случай, и отправляться нужно именно от него. Тогда наша задача примет вид: найти все числах, которые при делении на данное число b дают остаток с. Несмотря на кажущуюся простоту, такая постановка вопроса оказалась очень плодотворной. Её развил и превратил в стройную систему Гаусс (1777-1855 гг.), которому удалось сделать на этом пути много важных открытий.

К. Ф. Гаусс

Итак, нас интересуют все числа, дающие при делении на некоторое определённое число данный остаток. Если, например, число, на которое делят [его называют модуль^*], равно 7, а требуемый остаток равен 2, то искомыми числами будут:

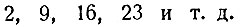
^* (Слово "модуль" происходит от латинского modulus (модулюс), что значит "мерка"; употребляется оно обычно в смысле "делитель". Постоянные, которые входят в знаменатель различных физических и технических формул, часто называются модулями: например, модуль упругости, модуль Юнга и т. д.)

Они образуют неограниченно продолжаемую арифметическую прогрессию, первый член которой равен 2, а разность - 7.

Числа, дающие при делении на модуль равные остатки, называют равноостаточными или сравнимыми по этому модулю. Следовательно, числа 2, 9, 16, 23 и т. д. сравнимы друг с другом по модулю 7. Точно так же числа 1 и 27 сравнимы по модулю 13, число 103 сравнимо с 3 по модулю 10.

Понятие сравнения, введённое Гауссом, нашло такое широкое применение в математике, что для него пришлось ввести специальное обозначение (его придумал тот же Гаусс). Если а и b при делении на m дают равные остатки, т. е. если а сравнимо с b по модулю m, то пишут:

читается это так: "а сравнимо с b по модулю m". Знак сравнения (≡) напоминает знак равенства. Это не случайно: свойства сравнений похожи на свойства равенств.

Кроме сравнений, содержащих известные, данные числа, например, 2≡5 (mod 3), 1000≡1 (mod 37) и т. д., приходится рассматривать сравнения, содержащие неизвестные. При этом возможны три случая: либо сравнение справедливо при любых целых значениях входящих в него букв, либо оно справедливо только при некоторых, либо оно не может быть справедливым ни при каких значениях входящих в него букв. Например, сравнение ах≡2а (mod а) справедливо при любых целых х и а (ах и 2а оба дают при делении на а остаток, равный нулю; значит, они сравнимы). Напротив, сравнение 2х≡3 (mod 5), справедливое при х = 4 (ибо 2*4=8 даёт при делении на 5 остаток 3), не выполнятся при х = 5, потому что тогда 2х равно 10; это число делится на модуль 5 без остатка. Наконец, сравнение 2х≡1 (mod 2) не выполняется ни при каком целом х: левая часть его (2х) делится на модуль, а правая - нет.

Решить сравнение, значит - найти все удовлетворяющие ему значения неизвестных (или доказать его невозможность). Сами значения неизвестных, удовлетворяющие сравнению, называются его решениями.

Сравнения, как и уравнения, могут быть первой, второй и т. д. степени, могут содержать одно, два и т. д. неизвестных. Вот несколько примеров сравнений:

Рассмотрим простейшие свойства сравнений. Возьмём сравнение a≡b (mod m) и попробуем "перевести" его на привычный нам язык равенств. Это нетрудно сделать. Ведь сравнение a≡b (mod m) обозначает, что а - b делится на m без остатка, т. е. что a - b равно произведению m на произвольное целое число n. Обратно: если а - b = mn, где n - целое число, то при делении а на m и b на m получатся одинаковые остатки. В самом деле, допустим, что при делении на m число а даёт остаток r₁, а число b - остаток r₂. Это значит, что имеют место равенства: а = pm+r₁, b = qm + r₂, где р, q, r₁ и r₂ - числа целые, а r₁ и r₂, кроме того, оба меньше m. Допустим, что r₁>r₂. Вычитая второе равенство из первого, получим:

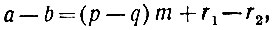
или

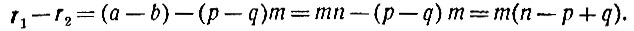
Следовательно, разность r₁-r₂ есть число, кратное m. Эта разность меньше m, потому что и уменьшаемое и вычитаемое - положительные числа, меньшие m; значит, она может быть равна только нулю, и значит, r₁=r₂. Но равноостаточность а и b по модулю m записывается как раз так: a≡b (mod m).

Итак, равенство а - b = mn (или а = b + mn) и сравнение а≡b (mod m) обозначают совершенно одно и то же. Где нужно, можно вместо равенства писать сравнение, где нужно - вместо сравнения равенство. То и другое выражают одну мысль, только, так сказать, на разных языках.

Покажем теперь, что сравнения по одному и тому же модулю можно складывать, вычитать и перемножать (левую часть - с левой, правую - с правой). Рассмотрим два сравнения:

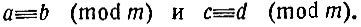
Первое, как мы знаем, равносильно равенству а = mn₁ + b, а второе равенству с = mn₂ + d; сложив (или вычтя) эти равенства, мы будем иметь: а±с = m(n₁±n₂)+b±d; переведя результат на язык сравнений, мы получим:

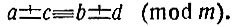
А это как раз и значит, что сравнения можно почленно складывать (и вычитать).

Если равенства а = mn₁ + b и с = mn₂ + d мы перемножим, то получим:

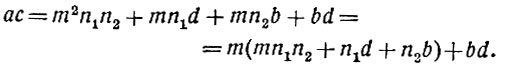
Обозначая выражение в скобках, которое, очевидно, является целым числом, одной буквой n, мы будем иметь:

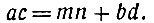
Это значит, что ac≡bd (mod m), т. е. что сравнения по одному и тому же модулю можно перемножать. Разумеется, складывать и перемножать можно не только два, но и любое число сравнений. Отсюда сейчас же получается следствие: сравнение, не содержащее неизвестных, можно возвести в любую степень^*.

^* (Умножение на выражение, содержащее неизвестное, как и в случае обыкновенных уравнений, может привести к посторонним решениям.)

Так же просто можно показать, что к обеим частям сравнения можно прибавить, от обеих частей отнять одно и то же число и обе части умножить на одно и то же число^*. Например, из a≡b (mod m) следует a+c≡b+c (mod m). Действительно, сложим сравнения

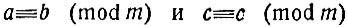
(первое дано, а второе - очевидно), получим а+c≡b+с (mod m), что и требовалось доказать.

^* (Умножение на выражение, содержащее неизвестное, как и в случае обыкновенных уравнений, может привести к посторонним решениям.)

Указанные свойства сравнений позволяют производить над ними почти все преобразования, которые мы производим над уравнениями. В частности, можно переносить члены с одной стороны (или, лучше сказать, из одной части) сравнения в другую, изменив, разумеется, знаки на обратные. Это, вместе с приведением подобных членов, позволяет приводить все сравнения к виду:

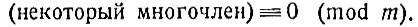
Например, сравнение

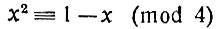
приводится к виду

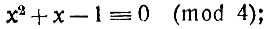
сравнение

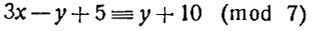
- к сравнению

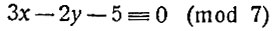
и т. д. В частности, любое сравнение первой степени с одним неизвестным можно привести к виду

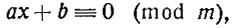
где a, b и m - заданные целые числа (m, кроме того, положительно).

Но в некотором отношении сравнения всё-таки "хуже" равенств. Сокращать их на общий множитель можно не всегда. Рассмотрим этот вопрос внимательнее.

Сравнение 22≡12 (mod 5), несомненно, справедливо: и 22 и 12 при делении на 5 дают остаток 2. Если мы разделим обе его части на 2, то получим 11≡6 (mod 5); это тоже справедливо: и 11 и 6 при делении на 5 дают в остатке 1. Кажется всё благополучно. Вот, однако, другой пример: 14≡10 (mod 4); действительно, и 14 и 10 при делении на 4 дают в остатке 2. Если же мы разделим обе части сравнения на 2, то получим 7 ≡ 5 (mod 4), что неверно: ведь 7 при делении на 4 даёт остаток 3, а 5 - единицу. В чём же дело?

В первом примере оба члена сравнения взаимно-просты с модулем. Во втором же оба члена и модуль имеют общий множитель, именно 2. Это и привело во втором примере к неблагополучию^*.

^* (Вопрос читателю: может ли одна часть сравнения быть взаимно-простой с модулем, а другая-нет? )

Сформулируем наши наблюдения в форме теорем и докажем их.

Теорема первая. Если обе части сравнения взаимно-просты с модулем и имеют общий множитель, то сравнение можно сократить на этот множитель.

Пусть в сравнении

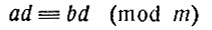
обе части делятся на d, а модуль не только не делится, но и взаимно-простой, т. е. не имеет делителей, общих с d и неравных 1. Из данного сравнения следует:

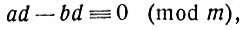
т. е. d(a - b) должно делиться на m. Но d, по условию, взаимно-просто с m. Следовательно, а - b должно делиться на m, т. е. должно иметь место сравнение а ≡ b (mod m), что и требовалось доказать. И здесь приходится использовать теорему третью главы VI (на стр. 58).

Теорема вторая. Если обе части сравнения и модуль имеют общий множитель, то справедливо сравнение, которое получается путём деления обеих частей данного сравнения и его модуля на этот общий множитель. (Иными словами, в этом случае можно сокращать обе части сравнения, но одновременно - и модуль.)

Возьмём сравнение

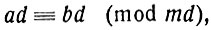
в котором обе части и модуль делятся на d. Переводим мысль, выраженную сравнением, на язык равенств:

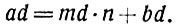
Сокращение этого равенства на d даёт

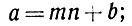
а это, в переводе на язык сравнений, значит:

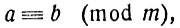
что и требовалось доказать.

Доказанная только что теорема объясняет, почему второй пример 14≡10 (mod 4) привёл нас при сокращении к абсурду. Обе стороны этого сравнения и его модуль (4) делятся на 2. Значит, нужно было не забыть сократить на 2 и модуль, что дало бы 7 ≡ 5 (mod 2), а это, очевидно, справедливо (и 7 и 5 при делении на 2 дают в остатке 1).

Но если, с точки зрения возможности сокращения, сравнения "хуже" равенств, то у них есть и такие свойства, которые позволяют делать преобразования, невыполнимые в случае равенств. Вот важнейшее из этих свойств: к любой части сравнения можно прибавить, от любой части сравнения можно отнять любое число, кратное модулю.

Действительно, прибавим к обеим частям сравнения

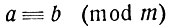
(или отнимем от них) очевидное сравнение cm≡0 (mod m); мы получим:

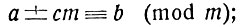
аналогично можно было бы получить:

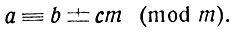
Посмотрим, какую пользу можно извлечь из этого свойства.

Возьмём сравнение

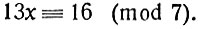(1)

Вычтем из левой части 7х: это - число, кратное модулю. Мы получим:

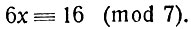
Далее, из правой части вычтем число 14, тоже кратное модулю. Получим:

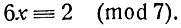
Сократив на 2 (модуль не делится на 2), мы получим совсем простое сравнение:

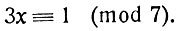(2)

Из сравнения (1) мы получили сравнение (2), справедливое при тех же значениях неизвестного х, при которых было справедливо исходное сравнение (1). Такие два сравнения называются эквивалентными, или равносильными. Но сравнение (2) проще сравнения (1) -в этом его преимущество.

Разберём несколько задач, при решении которых станет наглядной полезность сравнений.

Задача первая. Найти остаток от деления числа 1532⁵ - 1 на 9.

Для решения этой задачи не нужно делать утомительное умножение и скучное деление. Рассуждаем так:

11530 делится на 9 (сумма его цифр делится на 9); следовательно, 1532 даёт при делении на 9 остаток 2; это мы можем записать в форме сравнения

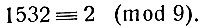
Мы знаем, что сравнения можно почленно перемножать; в частности, обе части сравнения можно возвести в одну и ту же степень. Возведём написанное сравнение в пятую степень; мы получим

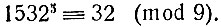
Вычтем из правой части 27 (число, кратное модулю):

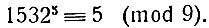
Если теперь от обеих частей сравнения отнять по единице, то получится

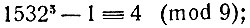
а это значит, что 1532⁵ - 1 даёт при делении на 9 остаток 4. Наша задача решена.

Задача вторая. Найти последние две цифры числа 9⁹⁹.

Рассмотрим сначала, каковы последние две цифры у первых десяти степеней девятки. Найти их просто:

Последнее число (9¹⁰), оканчиваясь на 01, даёт при делении на 100 в остатке единицу, что мы теперь умеем записать так:

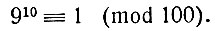
Если мы возведём обе части этого сравнения в произвольную целую степень р, то увидим, что всякая степень числа 9¹⁰, т. е. число 9^10р, будет сравнима с 1 по модулю 100.

Рассмотрим, далее, произвольную степень девяти 9^N. Обозначим число десятков в N через р, число единиц - через q; иными словами, положим N = 10p + q. Мы только что доказали, что

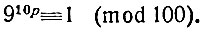
Умножив обе части этого сравнения на 9^q, получим слева

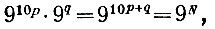
а справа 9^q, т. е.

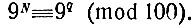
Последнее равенство показывает, что любая степень девяти (N) сравнима по модулю 100 с такой степенью девяти, показатель которой (q) равен остатку от деления первоначально данного показателя на 10, т. е. обе эти степени девяти имеют те же две последние цифры^*. Таким образом, наша задача упрощается. Последние ; две цифры числа 9⁹⁹ обязательно должны быть те же, что и у числа 9^a, где а - остаток от деления "двухэтажного" показателя 9⁹ на 10. Но остаток от деления любого числа на 10 равен последней цифре десятичной записи этого числа. Для числа 9⁹ он равен 9 (см. табличку степеней девятки, данную выше).

^* (Если два числа сравнимы, т. е. равноостаточны по модулю 100, то это значит, очевидно, что у одного из них в десятичной записи те же последние две цифры, что и у другого.)

Следовательно, 9⁹⁹ = 9⁹ (mod 100), т. е. 9⁹⁹ и 9⁹ имеют те же последние две цифры. Смотрим снова в табличку первых десяти степеней девятки: видим, что 9⁹ оканчивается на 89. Значит и 9⁹⁹ оканчивается на 89.

После вопроса о преобразованиях сравнений и действиях над ними было бы естественно заняться решением сравнений первой степени с одним неизвестным. Но мы этого делать не будем. Заметим только, что решение любого сравнения может быть сведено к решению неопределённого уравнения. Возьмём, например, сравнение

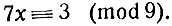
Это сравнение показывает, что разность 7х -3 делится на 9, т. е. равна произведению 9 на некоторое целое число y:

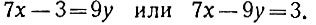
Получилось неопределённое уравнение, которое мы умеем решать в целых числах (см. предыдущую главу).

Взглянем теперь на сравнения с совершенно новой точки зрения. Зададим какой-нибудь определённый модуль, например, m = 5. При делении любого числа на 5 могут получиться следующие остатки: 0, 1, 2, 3 и 4. Все натуральные числа можно разбить на пять категорий, в зависимости от того, какой остаток получается при делении этих чисел на 5. Числа каждой категории образуют неограниченно продолжаемую арифметическую прогрессию с разностью, равной модулю, т. е. в нашем примере пяти. Вот эти пять прогрессий:

Ясно, что каждое число непременно войдёт в одну, и только в одну, из этих прогрессий. Такие прогрессии называют классами по модулю пять. Аналогичным путём все натуральные числа можно разбить на классы и по любому другому модулю.

Все числа, входящие в состав написанных выше прогрессий (т. е. все без исключения числа натурального ряда), называются вычетами^* по модулю 5; каждый из них может служить свободным членом сравнения х ≡ а (mod 5), имеющего решения.

^* (Слово "вычет" должно напоминать о том, что при изучении целых чисел мы смотрим на деление, как на повторное вычитание.)

Если бы мы взяли сравнение второй степени, например,

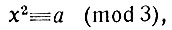
то убедились бы, что некоторые числа, например а = 1, являются вычетами, потому что уравнение х² ≡ 1 (mod 3) имеет решения; другие числа, например 2, не являются вычетами: можно доказать, что сравнение х² ≡ 2 (mod3) совсем не имеет решений. Говорят, что 2 есть квадратичный невычет по модулю 3. Для сравнений первой степени каждое натуральное число есть вычет.

Возьмём из каждого класса, т. е. из каждой прогрессии, написанной выше, по одному числу; например, возьмём следующие числа:

Взятые таким образом числа называются представителями классов по модулю пять, а их совокупность - полной системой вычетов по модулю 5.

Полная система вычетов по данному модулю обладает многими замечательными свойствами. Мы рассмотрим

? одно из них; чтобы оно стало нагляднее, сделаем ещё упрощение. Именно, вместо взятых наудачу представителей классов, возьмём в качестве таковых наименьшие положительные вычеты, соответствующие различным классам. В нашем примере это будут числа: 1, 2, 3, 4, 5. Заменим последний вычет, равный модулю, сравнимым с ним по этому модулю числом 0. Получим следующую систему чисел:

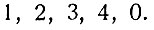
Будем над числами такой системы производить сложение, вычитание и умножение по обычным правилам, но каждый полученный результат заменять наименьшим положительным вычетом того же класса. Сложив, например, 3 и 4, мы получим 7; наименьший вычет класса, представителем которого служит 7, равен 2. Поэтому напишем: 3 + 4 = 2. Чтобы эта запись не слишком резала глаза, будем указывать модуль, по которому все числа были разбиты на классы. Будем писать: 3 + 4 = 2 (mod 5). Точно так же, помножив 2 на 3, получим 6; число 6 принадлежит первому классу по модулю 5; оно по этому модулю сравнимо с единицей. Поэтому будем писать: 2×3 = 1 (mod 5). Чтобы вычесть четыре из трёх, заменим тройку ближайшим большим представителем того же класса -восьмёркой. Получим 8 - 4 = 4, или, по модулю 3,

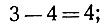
проверяем: если 3 - 4 = 4, то 4 + 4 (сумма разности и вычитаемого) должна равняться 3; и в самом деле, 4 + 4 равно 8, т. е. числу, сравнимому с 3 по модулю 5.

Ясно, что при таком соглашении, в результате действий над числами системы наименьших неотрицательных вычетов по некоторому модулю, мы всегда будем получать числа той же системы. Важнее другое: все свойства действий (сложения, вычитания и умножения) полностью сохраняются. Сохраняются переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, сохраняются все правила действий со скобками. Более того, оказывается, что каждое уравнение первой степени с одним неизвестным имеет решение, принадлежащее той же системе вычетов. Получается своеобразная арифметика, очень похожая на обычную, но, во-первых, без действия деления, а, во-вторых, и это главное, не с бесконечным множеством чисел, а только с ... пятью!

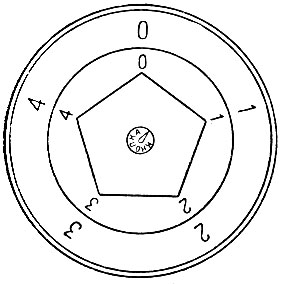
Рис. 6

Можно сделать своеобразные "счёты", наглядно иллюстрирующие эту арифметику. Вырежем из картона два кружка, один побольше, другой поменьше. На каждом из них в вершинах правильного вписанного пятиугольника напишем цифры 1, 2, 3, 4, 0, наложим меньший кружок на больший так, чтобы центры их совпали, и скрепим кружки кнопкой (рис. 6). Теперь для сложения двух чисел поступаем так: замечаем на большем кружке слагаемое и ставим против него нуль меньшего кружка. На меньшем кружке мысленно отмечаем второе слагаемое. Против него на большем кружке и будет сумма. Сложим, например, 2 и 4. Против двойки большего кружка ставим нуль малого (рис. 7). Четвёрке малого кружка соответствует единица большего Значит по модулю пять, 2 + 4=1.

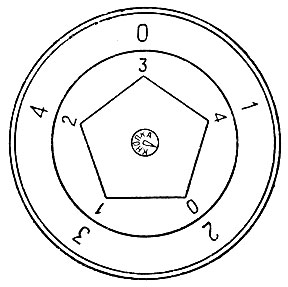
Рис. 7

Чтобы умножить 4 на 3, поступаем так. Сначала поставим оба кружка в исходное положение (т. е. чтобы одинаковые числа стояли друг против друга). Затем поворачиваем 3 раза (т. е. число раз, равное множителю) меньший кружок на угол, равный ⁴/₅ окружности (здесь числитель равен множимому, а знаменатель - модулю), и смотрим, против какого числа большего кружка станет нуль меньшего (рис. 8). Видим, что он придётся против двойки. Значит, в этой арифметике 4×3 = 2.

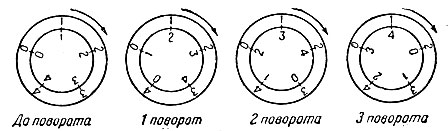
Рис. 8

Пользуясь этими "счётами" (или обычными сложением 1 умножением с последующей заменой результатов наименьшими соответствующими им вычетами по модулю 5), получим такие таблицы сложения и умножения (по модулю 5):

Из этой таблицы умножения мы видим, что 3×3 = 4; мы нашли ту арифметику, которая была обещана в начале главы.

В наших примерах мы имели дело с системами чисел, в которых установлены только три действия: сложение, вычитание и умножение. Такие числовые системы называются в математике "кольцами". Совокупность всех целых чисел (положительных и отрицательных, включая нуль) тоже образует кольцо, но это кольцо содержит бесконечное множество элементов. Кольцом же является совокупность всех многочленов всевозможных степеней относительно единственной буквы х с целыми коэффициентами: сумма, разность и произведение многочленов подобного рода являются, в свою очередь, такими многочленами; деление же, напротив, приводит сплошь да рядом к алгебраическим дробям. Совокупность натуральных чисел не является кольцом, потому что разность двух натуральных чисел может и не быть натуральным числом: например, 5 - 8 = - 3, а "минус три" - число хотя и целое, но не натуральное.

Кроме числовых систем с тремя действиями, можно рассматривать системы, в которых выполняются все четыре действия, причём результатом всегда будет число той же системы. К таким системам относится совокупность всех рациональных (т. е. и целых и дробных) чисел: их сумма, разность, произведение и частное оказываются тоже рациональными числами. Подобные числовые системы называются полями, или телами. Говорят, что все рациональные числа образуют поле (тело). Все действительные числа, т. е. рациональные и иррациональные вместе, также образуют поле; поле образует и совокупность комплексных чисел. При изучении полей, как и в обычной арифметике, "строго воспрещается" делить на нуль.

Кроме колец и тел, рассматривают иногда числовые системы, в которых осуществимы только два действия: сложение и вычитание. Умножение и деление могут дать числа, не принадлежащие к изучаемой системе. Такие системы называют группами.

Говоря о кольцах, мы упомянули вскользь о "кольце многочленов". Это выражение кажется бессмысленным, потому что мы сказали сейчас, что кольцом называют некоторую совокупность чисел, а многочлены числами Вне являются. Но дело в том, что к группам, кольцам и телам можно подойти шире, рассматривая не только системы чисел, но и системы любых вещей, знаков, величин, над которыми производятся какие-то действия. Изучением групп, колец и тел различной природы, т. е. систем с двумя, тремя или четырьмя действиями, независимо от вещей, из которых они построены, занимается Высшая Алгебра. Арифметика, напротив, в первую очередь интересуется свойствами самих чисел. Эта её черта особенно ярко проявляется в учении о простых числах, которыми мы займёмся в следующих главах.