Глава VII. Уравнения, которыми занимается арифметика

Название этой главы может вызвать недоумение: ведь уравнениями занимается алгебра; какие же могут быть уравнения в арифметике? Но, оказывается, есть особый род уравнений, вернее, особая точка зрения на некоторые уравнения, по самой сути дела, по самому духу своему стоящая к арифметике гораздо ближе чем к алгебре. Что же это за уравнения?

Число и наука о нем

Рассмотрим следующую простую задачу.

В артели было несколько квалифицированных рабочих и несколько чернорабочих. Каждый квалифицированный рабочий получает за работу 210 р., а каждый чернорабочий - 150 р. Всего артель получила 1740 р. Сколько в артели было квалифицированных рабочих и сколько чернорабочих?

Уравнение этой задачи составляется очень просто: если квалифицированных рабочих было x, а чернорабочих y, то первые получили 210x, а последние - 150y рублей. Сумма этих количеств должна равняться общему заработку артели; это сразу даёт уравнение:

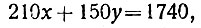
или, по сокращении на 30,

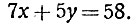
Но дальше получается неприятность: никаких данных Для составления второго уравнения нет. В аналогичных задачах, которыми пестрят и "Шапошников - Вальцов" и другие задачники, всегда даётся некоторое дополнительное условие: или общее количество рабочих, или отношение числа квалифицированных к числу неквалифицированных, или что-нибудь ещё в этом роде. Тогда можно составить второе уравнение и без труда решить полученную простую систему. В нашем примере данных для составления второго уравнения нет. Нужно решать единственное уравнение:

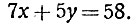
С точки зрения алгебры вопрос ясен: уравнение имеет бесчисленное множество решений; каждому произвольно взятому числу x соответствует определённое число y, которое вычисляется по формуле

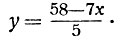
Но такое решение задачи нас удовлетворить не может. Ведь число рабочих каждой категории должно быть целым положительным (в крайнем случае, одно из неизвестных может равняться нулю - артель может состоять из рабочих одной категории).

Таким образом, из бесконечного множества решений уравнения 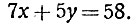нас интересуют только такие пары значений x и y, когда оба неизвестных являются натуральными числами (легко видеть, что при x = 0 или y = 0 второе неизвестное получается дробным, а потому нулевые решения можно не рассматривать). Это позволит выделить некоторое определённое решение и довести задачу до конца.

Будем давать неизвестному x целые значения и вычислять соответствующие значения y. Проб придётся сделать не так уж много, потому что при x>8 второе неизвестное станет отрицательным, а такое решение нас не устраивает. Составляем табличку:

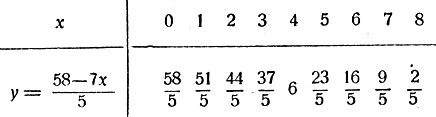
Только при х = 4 второе неизвестное получает целое положительное значение (y = 6). При любом другом значении икса число y будет либо дробным, либо отрицательным. Следовательно, задача имеет одно единственное, вполне определённое решение:

Дополнительное условие (целочисленность решения) заменило нам второе уравнение.

Разобранная задача привела к одному уравнению с двумя неизвестными. Возможны и такие задачи, в которых одно уравнение связывает больше чем два неизвестных. Некоторые задачи приводят к системам с числом уравнений, меньшим числа неизвестных. Подобные уравнения или системы уравнений называются неопределёнными, потому что, если нет дополнительных условий, они имеют бесконечное множество решений: одному или нескольким неизвестным можно дать любые значения; тогда уже определяются значения остальных. Неопределённые уравнения с их бесконечным числом решений весьма полезны в высшей математике при изучении кривых линий и поверхностей.

Иначе обстоит дело в том случае, когда искомые величины, помимо неопределённого уравнения, должны удовлетворять добавочным условиям. Наиболее важным и изученным является тот случай, когда разыскиваются целые решения. В нашем примере это как раз и было. Чаще, правда, разыскиваются не только натуральные, но все целые решения -как положительные, так и отрицательные. Иногда, напротив, на решения накладываются ещё более жёсткие ограничительные условия.

Такого рода исследование неопределённых уравнений носит название неопределённого анализа. Оно называется также диофантовым анализом по имени замечательного греческого математика - Диофанта, жившего в III в. н. э. в городе Александрии (больше о его Жизни ничего неизвестно). Диофант оставил книгу, на которой воспитывались творцы современной Теории Чисел. Нужно заметить, что он занимался разысканием не только целых, но и рациональных (т. е. целых и дробных) решений неопределённых уравнений. Решением неопределенных уравнений в целых числах и исследованием полученных решений стали значительно позже заниматься индусы. Впрочем, трудно сказать, когда впервые возник неопределённый анализ; во всяком случае, в XII в. н. э, у индийского математика Бхаскара Акарья мы встречаем вполне разработанную методику целочисленного решения неопределённых уравнений первой степени.

К задачам неопределённого анализа индусов привели вопросы практической жизни. При решении различных задач, связанных с календарём, им часто приходилось разыскивать некоторый промежуток времени, содержащий как целое число лет, так и целое число суток. Это приводило к неопределённым уравнениям, у которых интерес представляли только целые решения.

Разберём несколько задач на неопределённые уравнения, чтобы выяснить основные их особенности; ограничимся при этом уравнениями первой степени, потому что решение неопределённых уравнений высших степеней,хотя бы. даже второй, представляет значительные трудности.

Задача первая. Требуется пятирублёвку разменять полтинниками^*, двугривенными и пятачками так, чтобы всего было 20 монет.

^* (Полтинник - раньше употреблявшаяся монета в 50 кошек.)

Составляем уравнение. Пусть х - число пятачков, y - число двугривенных, z - число полтинников. Тогда общая сумма, равная 500 копеек, выразится так: 5х + 20y + 50z; с другой стороны, по условию, x + y + z = 20. Больше никаких данных нет. Следовательно, решение задачи сводится к решению в целых числах системы:

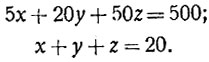
Число неизвестных (три) больше числа уравнений (два); значит, система уравнений - неопределённая. Сократив первое уравнение на 5 и вычтя из него второе, получим единственное уравнение с двумя неизвестными:

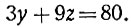
Остаётся решить это уравнение в целых числах. Но приглядываясь к нему внимательнее, мы видим, что при любых целых значениях y и z левая часть уравнения должна делиться на 3; правая же часть (80) на 3 не делится. Следовательно, не существует таких целых y и которые удовлетворяли бы нашему уравнению. Это - пример неопределённого уравнения, неразрешимого в целых числах. Поэтому неразрешима и приведшая к нему задача. Разменять пятирублёвку двадцатью монетами указанного достоинства невозможно.

Задача вторая. Найти натуральное число, которое при делении на 3 даёт остаток 2, а при делении на 5 - остаток 3.

Обозначим искомое число через х. Если частное от деления х на 3 обозначим через y, а частное от деления на 5 - через z, то получим (см. стр. 60):

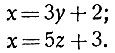
По смыслу задачи х, y и z должны быть целыми (больше того - натуральными) числами. Значит, нужно решить в целых числах неопределённую систему уравнений.

Разыскание самого числа х не вызывает затруднений. При любых целых y и z будет целым и х. Поэтому приходится решить следующее единственное уравнение с двумя неизвестными:

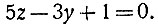
Найдя все целые положительные значения y или z из этого уравнения, сразу получим и все целые положительные значения х.

Из уравнения 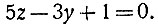находим:

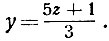
Одно решение очевидно: при z = 1 получим

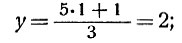
и z и y получаются целые. Им соответствует решение х = 8.

Найдём все остальные решения. Для этого введём вспомогательное неизвестное u, полагая z = 1 + u. Мы получим;

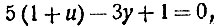
т. е.

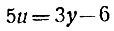
или

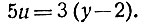
Правая часть последнего уравнения при любом целом y делится на 3. Значит, и левая должна делиться на 3. Но число 5 -взаимно-простое с числом 3; поэтому и должно разделиться на 3^*, т. е. иметь вид 3n, где n - целое число. В этом случае у будет равняться

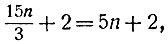
т. е. тоже целому числу. Итак, z = l+ u = 1 + 3n, откуда

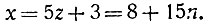
^* (Вспомним теорему третью предыдущей главы (стр. 58))

Получилось не одно, а бесконечное множество значений для х, т. е. решений нашей задачи:

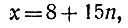
где n - целое число (положительное или нуль);

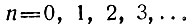
Проверка показывает, что все эти решения годятся^*.

^* (Все решения этой задачи образуют неограниченно продолжаемую арифметическую прогрессию с первым членом 8 и разностью 15:

)

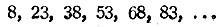
Задача третья. Куплены апельсины по 7 р. и мандарины по 4 р., всего на сумму 53 р. Сколько куплено апельсинов и сколько мандаринов?

Одно уравнение составляется сразу; вот оно:

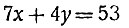
(через х обозначено число апельсинов, а через y - мандаринов).

По смыслу задачи ясно, что х и y должны быть одновременно целыми положительными числами. Имеем

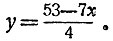
Даем х значения от 1 до 7 (при х>7 для у получатся отрицательные значения). Вычисляем соответствующие значения y:

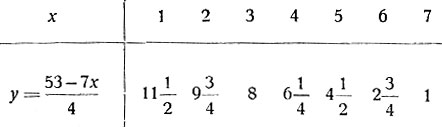
Получаются два решения задачи:

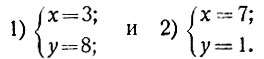
Во всех остальных случаях хотя бы одно из неизвестных дробно или отрицательно. Следовательно, задача имеет два решения: либо куплено 3 апельсина и 8 мандаринов (это стоит 3*7 + 8*4 = 53 р.), либо 7 апельсинов и 1 мандарин (это стоит 7*7+ 1*4, т. е. тоже 53 р.).

Итак, в задачах на неопределённые уравнения мы сталкиваемся с самыми разнообразными случаями: задача может быть совсем неразрешимой, может иметь бесконечное множество решений, может иметь несколько определённых решений; в частности, она может иметь одно единственное решение.

Отметим разницу во взглядах на решение уравнения: с одной стороны - в алгебре, с другой - в неопределённом анализе. В алгебре господствует стремление охватить уравнение возможно шире, найти все мыслимые его решения. Для того чтобы сделать алгебраические уравнения разрешимыми во всех случаях, приходится вводить новые виды чисел: иррациональные, комплексные. В неопределённом же анализе рассматриваются только целые числа. Правда, от отрицательных чисел в неопределённом анализе отказаться нельзя,- без них пришлось бы рассматривать слишком много частных случаев, а употребление отрицательных чисел позволяет получить очень удобные общие формулы. Но так как в неопределённом анализе рассматриваются только целочисленные решения, то для их нахождения можно использовать свойства целых чисел: делимость, кратность, разложение на простые множители, нахождение общего наибольшего делителя и так далее. Это - понятия, относящиеся не к алгебре, а к арифметике. Поэтому неопределённый анализ рассматривается обычно не как раздел алгебры, а именно как раздел арифметики. Таким образом, оправдано название настоящей главы этой книги.

Перейдём к более внимательному разбору неопределённого уравнения первой степени с двумя неизвестными. После обычной "обработки", которой принято подвергать уравнение (освобождение от знаменателей, приведение подобных членов и т. д.), такое уравнение может быть записано в виде

(*)

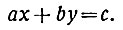Здесь а, b, с -данные целые (положительные или отрицательные) числа; х и y - неизвестные, но принимающие только целые значения (тоже - положительные, отрицательные или нуль).

Рассмотрим прежде всего случай, когда неопределённое уравнение неразрешимо (как в разобранной выше задаче первой на стр. 74).

Найдём общий наибольший делитель чисел а и b. Обозначим его через d (если а и b - взаимно-простые числа, то d равно 1). Тогда а будет равно произведению d на некоторое целое число m, а b - произведению того же d на целое число n:

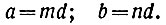
При этом тип обязательно будут числами взаимно-простыми. В самом деле, если бы они, в свою очередь, имели общий делитель k, не равный единице, то произведение kd было бы делителем и числа а, и числа b, а потому d не было бы наибольшим делителем этих двух чисел.

Каковы бы ни были целые числа х и y, левая часть уравнения (*) должна делиться на d, потому что оба слагаемых ах и by на него делятся. Значит, и правая часть этого уравнения должна делиться на d. Отсюда можно сделать такой вывод: если свободный член неопределённого уравнения не делится на общий наибольший делитель коэффициентов при неизвестных, то уравнение (*) неразрешимо. В задаче первой на стр. 74 мы пришли к уравнению:

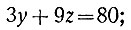
здесь общий наибольший делитель коэффициентов равен 3; свободный же член (80) на 3 не делится; следовательно, уравнение неразрешимо. Мы видели, что задача первая действительно не имеет решений.

Если нам даётся неопределённое уравнение (*), то мы прежде всего должны посмотреть, не принадлежит . ли оно к случаю, который только что рассмотрен. Если принадлежит, то мы говорим, что это уравнение не может иметь никаких целочисленных решений, и больше нам с этим уравнением делать нечего. Таким образом, мы можем считать достойными изучения только такие уравнения, все члены которых делятся на общий наибольший делитель - коэффициентов при неизвестных. Тогда мы можем все члены уравнения сократить на этот делитель. Получится уравнение, у которого коэффициенты при неизвестных - числа взаимно-простые. Поэтому в дальнейших рассуждениях мы будем считать, что в уравнении

(*)

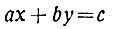числа а и b не только целые, но и взаимно-простые. Уравнения первой степени называют иначе линейными уравнениями^*. Уравнения, все члены которых имеют одинаковое измерение, т. е. одинаковую сумму показателей при неизвестных, называют однородными. Например, уравнения x² + 2xy = y² или x³ + y³ = 3xy² будут однородными. Однородные уравнения обладают многими интересными свойствами и решаются они обычно проще неоднородных. В случае линейных уравнений однородным будет уравнение, не содержащее свободного члена, который является членом нулевого измерения. Например, уравнения

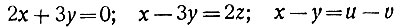
будут однородными; уравнения же

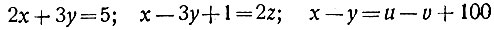
- неоднородные.

^* (Это название происходит оттого, что в аналитической геометрии (отдел, с которого обычно начинают изучение высшей математики) уравнение ах + by + с изображает прямую линию.)

Рассмотрим в качестве первого примера такие два уравнения:

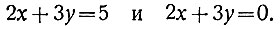
У этих уравнений одинаковые коэффициенты при неизвестных. В этом случае второе уравнение называют однородным уравнением, соответствующим первому (неоднородному) уравнению. Занимаясь линейным неопределённым уравнением ах + by = с, естественно сначала рассмотреть однородное уравнение, т. е. положить с = 0:

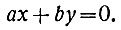
Удобнее записать это уравнение так:

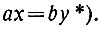
^*) (Читателю, быть может, не нравится, что вместо ах = - by мы написали ах = by. По существу, конечно, сделано следующее. Сначала написано ах = -by. Затем положено: b₁ = -b, что даёт ах = b₁y. Наконец, b₁, обозначающее совершенно произвольное число, заменено буквою b.)

Решить его очень просто. Раз правая часть (by) делится на b, значит и левая (ах) должна делиться на b. Но а - число взаимно-простое с b; следовательно, х должен быть кратным b (вспомним теорему третью предыдущей главы на стр. 58).

Итак,

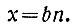
Чтобы найти y, мы подставляем найденное выражение для х в уравнение ах = by. Получим:

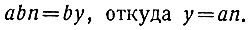
Здесь n должно быть непременно то же самое, что в выражении для х.

Следовательно, решение нашего однородного уравнения имеет вид:

(**)

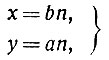где n - любое целое число. Обратно, при любом целом n найденные выражения для хну будут целыми и будут обращать данное уравнение в тождество. Следовательно, формулы (**) полностью решают однородное уравнение.

Те задачи, которые впервые привели индийских астрономов к неопределённым уравнениям (о чём упоминалось на стр. 74, в начале этой главы), приводили как раз к однородным уравнениям.

С однородными неопределёнными уравнениями нередко приходится иметь дело и современной технике. В качестве примера приведём вопрос о числе зубцов у зубчатых колёс. Для плавной работы пары сцепленных зубчатых колёс необходимо, чтобы числа их зубцов были обратно пропорциональны числам оборотов каждого из колёс в единицу времени. Например, если одно из колёс делает 50, а другое - 80 оборотов в минуту, то число х зубцов первого колеса должно относиться к числу y зубцов второго, как 80 к 50; это записывается так:

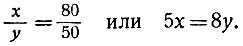
Получилось однородное уравнение, которое легко решается в целых числах. По формулам (**)

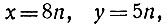
где n - любое целое число.

Переходим теперь к неоднородным неопределённым уравнениям первой степени, т. е. к уравнениям вида

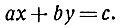
Все решения такого уравнения можно, как мы увидим, записать в виде двух формул, содержащих произвольное целое число n (подобно формулам (**) в случае однородного уравнения). Эти формулы мы будем называть общим решением уравнения (*), а каждую пару значений неизвестных, которая получается при некотором выбранном значении n,- частным решением. В однородном уравнении 5х = 8y решение

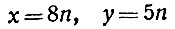
будет общим, а решение

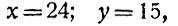
полученное из предыдущего при n = 3,- частным.

Предположим, что путём подбора удалось найти одно (частное) решение уравнения ах + by = с, т. е. найти два целых числа х₀ и y₀, удовлетворяющих соотношению

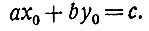
Применим приём, употребительный в алгебре и использованный нами в начале главы при решении числовых задач. Именно, введём новые вспомогательные неизвестные u и v, связанные с нашими прежними неизвестными-иксом и игреком, именно: положим

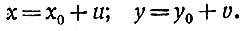
Подставляя эти выражения в уравнение ах + by = с, мы получим:

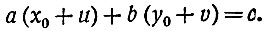
Раскроем скобки и перегруппируем иначе члены:

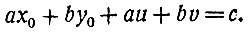
Вычитая из этого равенства тождество ах₀ + by₀ = с, получим:

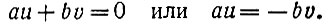
Это - однородное уравнение, соответствующее неоднородному уравнению ах + by = с. Его решение мы можем написать по формулам (**) сразу; вот оно:

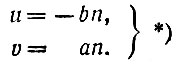
^*) (Здесь перед b стоит знак "минус", которого не было в формулах (**), потому что рассматриваемое уравнение имеет вид не au = bv, а au = - bv, у коэффициента b стоит знак "минус".)

Следовательно,

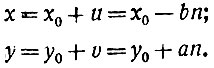
Такой вид должно иметь любое решение уравнения ах + by = с. С другой стороны, подставив найденные значения х и y в наше уравнение (*), мы убедимся, что при любом n они ему удовлетворяют. В самом деле:

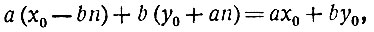
а это число равно с, так как x₀ и y₀ удовлетворяют уравнению (*).

Следовательно, мы нашли общее решение неоднородного уравнения.

Мы получили замечательный результат: общее решение линейного неоднородного уравнения равно сумме его частного решения и общего решения соответствующего однородного уравнения. Этот простой результат является, однако, очень важным. Достаточно сказать, что аналогичные теоремы встречаются в самых тонких отделах высшей математики.

Каким же образом найти числа x₀ и y₀, т. е. хотя бы одно решение неопределённого уравнения (*)? Практически, если коэффициенты a, b и с этого уравнения невелики, то лучше всего просто подобрать это решение, давая одному из неизвестных, например х, последовательно значения 0, 1, 2, 3,..., пока и для второго, y, не получится целое значение; мы так уже поступали при решении задачи третьей (стр. 76). Если же коэффициенты эти велики, то приходится в той или иной форме использовать алгоритм Евклида. Так, по существу, поступали уже индусы, так же поступают и современные математики. Как применить алгоритм Евклида к решению уравнения (*), лучше всего будет видно на числовом примере.

Требуется решить уравнение

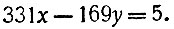
Найдём сначала какое-нибудь частное решение этого уравнения.

Постараемся свести данное уравнение к уравнению с меньшими коэффициентами. С этой целью делим больший коэффициент (331) на меньший (169). Получаем в частном 1 и в остатке 162. Значит,

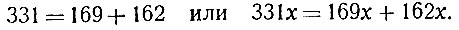
Наше уравнение можно теперь преобразовать так:

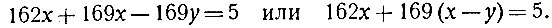
Введём вспомогательное неизвестное,- приём, которым мы уже пользовались,- именно, положим

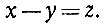(1)

Получим уравнение с меньшими коэффициентами:

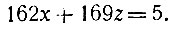
Заметим, что вспомогательное неизвестное 2 вошло в равенство (1), связывающее 2 со старыми неизвестными х и y, с коэффициентом 1. То же самое можно сказать и о неизвестном y, входившем в исходное уравнение с меньшим по абсолютной величине коэффициентом.

Повторяем с полученным уравнением снова тот же приём: делим его больший коэффициент при неизвестном на меньший; иными словами, делим меньший коэффициент исходного уравнения (169) на первый остаток (162). Получим в частном 1 и в остатке 7; иными словами, 169z = 162z + 7z. Наше уравнение переписывается так:

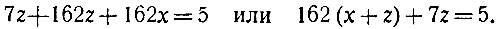
Вводим новое вспомогательное неизвестное, полагая:

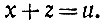(2)

[Обратим внимание на то, что в уравнении (2) и и (новое неизвестное), и х (то старое неизвестное, которое в предыдущем уравнении имело меньший коэффициент) имеют коэффициентом единицы!] Мы получим:

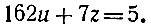
Делим снова больший коэффициент на меньший, т. е. делим первый остаток исходного уравнения (162) на второй его остаток; в частном получится 23, а в остатке 1. Следовательно, 162u = 7*23u + u, и наше уравнение примет вид:

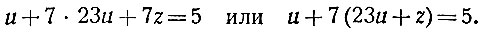
Введём последнее вспомогательное неизвестное, положив:

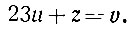(3)

(И здесь новое неизвестное v и одно из старых, z,- именно то, которое входило в предыдущее уравнение с меньшим коэффициентом, имеют коэффициент 1. Так будет всегда - читатель без труда докажет сам, почему.)

Наше уравнение примет теперь особенно простой вид:

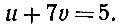
Полученное уравнение выгодно отличается от предыдущих тем, что коэффициент при одном из неизвестных равен 1. Это не случайное свойство нашего примера; так должно быть всегда. Действительно, пробежав глазами все строки нашего рассуждения, которые напечатаны курсивом, читатель убедится, что мы фактически вычисляли общий наибольший делитель двух коэффициентов при неизвестных в исходном уравнении, и цепочка наших действий окончится тогда, когда один из коэффициентов очередного уравнения станет равен этому общему наибольшему делителю. Вспомним теперь, что мы рассматриваем только такие уравнения, коэффициенты которых - взаимно-простые числа^*. Следовательно, их общий наибольший делитель равен 1, и последнее в цепи упрощённых уравнений обязательно будет иметь одним из коэффициентов единицу.

^* (Если они имеют общий делитель, отличный, от единицы, то как мы знаем, либо уравнение неразрешимо, либо его можно на этот делитель сократить.)

Последнее уравнение (u + 7v = 5) даёт нам;

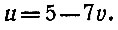
При любом целом v будет целым и u. Положив v равным, например, нулю, получим u = 5. Теперь остаётся пройтись "снизу вверх" по всем равенствам, отмеченным нумерами (3), (2), (1). При этом каждое подлежащее определению неизвестное будет иметь коэффициентом единицу (мы всё время обращали внимание на это обстоятельство!). Поэтому все неизвестные, в том числе и х, и y, будут целыми числами. В нашем примере мы получим:

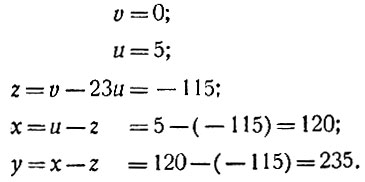
Итак, частным решением нашего уравнения будет

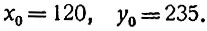
Мы уже видели, как найти общее решение этого уравнения. Для этого мы рассматриваем соответствующее однородное уравнение;

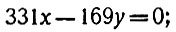
здесь а = 331, b = 169. Поэтому (см. формулы (**) на стр. 81) общим решением неоднородного уравнения 331х - 169y = 5 будет:

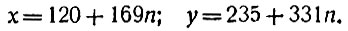
Этот приём решения несколько громоздок, но на нём стоило остановиться по двум причинам: во-первых, он ясно выявляет связь между решением неопределённого уравнения и алгоритмом Евклида; во-вторых, он показывает, что при любых взаимно-простых коэффициентах при неизвестных уравнение имеет решение. Практически такой приём не доводится до конца; получив вспомогательное уравнение со сравнительно небольшими коэффициентами, последнее решают подбором. Самый ход решения можно рационализировать; выкладки при этом упростятся, но существо дела замаскируется^*.

^* (Такой упрощённый путь решения неопределённого уравнения дан, например, во 11 части учебника алгебры Киселёва и в книге Я. Перельмана "Занимательная алгебра".)

Существуют готовые формулы решения неопределённого уравнения первой степени с двумя неизвестными, 1 но их вывод и применение основаны на использовании непрерывных дробей, с которыми читатель, быть может, незнаком. Заметим, что теория непрерывных дробей тоже связана с алгоритмом Евклида, так что и в этом случае без него обойтись нельзя.

Мы уже говорили, что первой книгой о неопределённых уравнениях было сочинение Диофанта (III в. н. э.). Есть основания полагать, что за 500 лет до Диофанта Архимед умел решать такие уравнения. В средние века ими занимались индусы и отчасти арабы. В Европе первым стал изучать целочисленные решения неопределённых уравнений французский математик Баше де-Мезириак, издатель и комментатор сочинений Диофанта (начало XVII в.).

Уже Диофант наряду с линейными уравнениями (уравнениями первой степени) рассматривал квадратные и кубичные неопределённые уравнения. Решение их, как правило, сложно. Остановимся на одной задаче, ставшей классической.

Вот эта задача: найти такие прямоугольные треугольники, все три стороны которых выражаются целыми числами.

Теорема Пифагора позволяет сразу составить уравнение для этой задачи. Если длины катетов мы обозначим через х и y, а гипотенузы - через z, то получим:

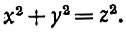
Это - неопределённое уравнение (уравнение одно, а неизвестных три). Оно однородное, второй степени. Одно его решение известно всем: катеты - 3 и 4, а гипотенуза - 5 единиц ("египетский треугольник"). Но знание частного решения позволяет решить полностью только линейные уравнения. Здесь же для полного решения придётся искать какой-то искусственный приём.

Будем искать три числа х, y, z, удовлетворяющие пифагорову^* уравнению и не имеющие ни одного общего множителя, кроме 1^**. Важно найти именно эти решения, потому что из любого "взаимно-простого" решения х₀, y₀, z₀ сейчас же получается серия составных решений nх₀, ny₀, nz₀, где n - любое целое число. Обратно: если найдём какое-нибудь "составное" решение р, q, r, то, полагая р = ах₀, q = ay₀, r = az₀, где а - общий наибольший делитель чисел р, q и r, подставив ах₀, аy₀, az₀ в уравнение и сократив его на a², убедимся, что х₀, y₀, z₀ образуют "взаимно-простое" решение. Таким образом, найдя все "взаимно-простые" решения, мы будем знать и все вообще решения пифагорова уравнения.

^* (Пифагор сам не занимался этим уравнением, но оно связано с теоремой Пифагора, и поэтому такое название уравнения оправдано.)

^** (Такие три числа называются, взаимно-простыми. Мы видим, что это название применяется не только к паре чисел, как на стр. 62, но и к тройке, четвёрке и большему количеству целых чисел.)

Но если х, y и z - взаимно-простые числа, то они не могут быть все три чётными. Два из них тоже не могут быть чётными, потому что тогда одна часть равенства будет делиться на 2, а другая нет. Все три нечётными быть не могут, потому что сумма двух нечётных чисел - четна. Следовательно, либо нечётны оба катета, либо нечётны один из катетов и гипотенуза.

Покажем, что оба катета не могут выражаться нечётными числами. Действительно, если один из них выражается числом 2q + 1, а другой - числом 2р + 1 (где q и р - целые числа), то сумма их квадратов равна

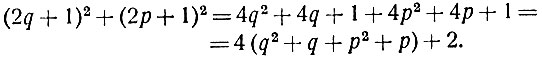
Эта сумма, очевидно, делится на 2 и не делится на 4. Но квадрат любого чётного числа делится на 4, а квадрат любого нечётного не делится на 2. Следовательно, сумма квадратов двух нечётных чисел не может быть ни квадратом чётного, ни квадратом нечётного числа, т. е. вообще не может быть квадратом целого числа.

Итак, если все три стороны прямоугольного треугольника выражаются взаимно-простыми целыми числами, то возможно только такое "распределение чётности": один из катетов -чётное число, а другой катет и гипотенуза - нечётные.

Будем чётный катет обозначать через х, а нечётный - через y; тогда мы вправе положить x = 2v, и наше уравнение запишется так: 4v² + y² = z², или так 4v² = z² - y², или, наконец, так:

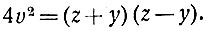
Сумма и разность двух нечётных чисел всегда четны. Положим поэтому

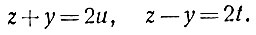
Нетрудно видеть, что u и v - числа взаимно-простые, причём одно из них чётное, а другое нечётное. Действительно, выразив z и у через и и t, получим: z = u + t, y = u - t. Если бы u и t имели общий делитель, то его имели бы и z, и y, что противоречит предположению об их взаимной простоте; точно так же u и v не могут быть одной чётности, потому что тогда z, равный их сумме, был бы чётным, что, как мы видели, невозможно. Подставляя в уравнение 4v² = (z+y)(z-y) вместо суммы и разности неизвестных числа 2u и 2v, мы получим:

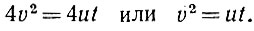
Но это возможно только в том случае, если u и t порознь являются квадратами, т. е. если u = a²; t = b². Действительно, в произведение ut (равное квадрату числа v) все простые множители входят парами^*. Если бы в u имелся какой-нибудь непарный множитель, то такой же множитель должен был бы быть и в t, чтобы в произведение ut = v² он вошёл парой. А это невозможно, потому что числа u и t взаимно-простые и общих множителей не имеют. Итак, в u все простые множители должны входить парами; то же можно сказать и про t. Следовательно, и u и t являются квадратами. Заметим ещё, что, в силу взаимной простоты и различной чётности чисел u( = а²) и t(= b²), сами числа а и b тоже будут взаимно-простые и различной чётности. Таким образом,

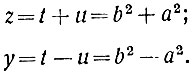
^* (Подробно о разложении на простые множители будет рассказано в главе XI (стр. 138).)

Получается следующий результат: гипотенуза прямоугольного треугольника с целочисленными взаимно-простыми сторонами обязательно должна быть суммой, а один из катетов - разностью квадратов двух одних и тех же целых чисел, тоже взаимно-простых и притом различной чётности. Но и обратно: сумма и разность квадратов любых целых чисел а и b даёт решение пифагорова уравнения, потому что в этом случае второй катет автоматически получается целым числом:

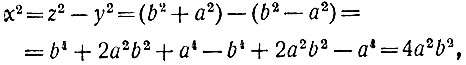
откуда

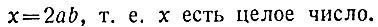
Следовательно, наиболее общее "взаимно-простое" решение пифагорова уравнения будет определяться формулами:

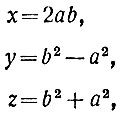
а все без исключения решения, как простые, так и составные,- формулами:

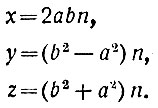
Здесь n - совершенно произвольное натуральное число, а а и b - любые целые числа, выбор которых ограничен "лишь следующими условиями: 1) b больше а, 2) b и а - взаимно-простые, 3) b и а - различной чётности.

Мы видим, что "выбор" получился больший, чем в тех случаях, которые мы до сих пор рассматривали. Оно и понятно. Там одно соотношение связывало два неизвестных, а здесь -три. Связь, ограничение, естественно, стали слабее.

Рассмотрим некоторые числовые решения пифагорова уравнения. Если n = 1 (решения "взаимно-простые"), то мы получим следующий ряд решений:

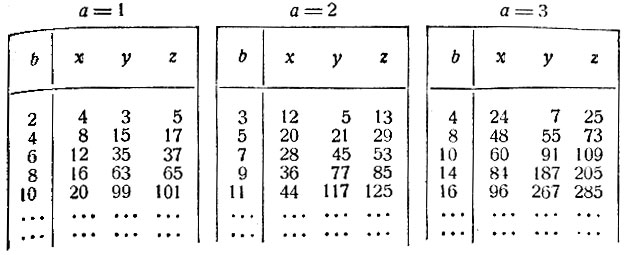
Далее можно написать таблички для а = 4, а = 5 и т. д.

Умножая любую строку (т. е. все числа строки) каждой из табличек на произвольное натуральное число, мы получим новые серии решений. Например, умножая третью строку второй таблички последовательно на 2, 3, 4,..., получим следующие решения:

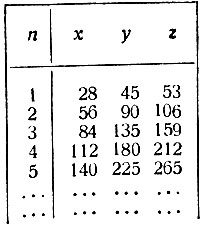
Никаких иных решений, кроме полученных этим путём из наших табличек, задача иметь не может.

После уравнения х² + y² = z² естественно рассмотреть уравнения x³+y³ = z³; х⁴+y⁴ = z⁴ и т. д. Математики XVI и начала XVII в. пытались решить эти уравнения в целых числах, но безуспешно.

Так обстояло дело до середины XVII в., когда француз Ферма, рассмотревший это уравнение в общем виде, т. е. в форме

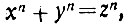
где n - любое целое число, пришёл к выводу, что при любом n, большем двух, задача неразрешима в целых числах (при n=1 её решит любой шестиклассник, а решение её при n = 2, т. е. решение пифагорова уравнения, мы только что разобрали).

Пьер Ферма (1601-1665 гг.), крупный юрист, видный общественный деятель своей родины -города Тулузы,- занимался математикой в часы досуга. О жизни его известно мало, книг он не печатал. Оставшиеся после него рукописи были изданы его сыном уже после смерти отца. Ферма состоял в переписке почти со всеми выдающимися математиками той эпохи; такой крупный учёный, как Паскаль, считал его лучшим математиком своего времени. Одновременно с Декартом Ферма заложил основы аналитической геометрии, вместе с Паскалем - основы теории вероятностей. Но лучшие его открытия принадлежат теории чисел.

П. Ферма

На полях книги Диофанта Ферми сделал следующую надпись (на латинском языке): "Ни куб на два куба, ни квадрато-квадрат и вообще никакая, кроме квадрата, степень, не может быть разложена на сумму двух таких же; я нашёл удивительное доказательство этому. Однако ширина полей не позволяет здесь его осуществить".

Эту теорему Ферма оставил недоказанной. И не только эту: Ферма формулировал много интересных теорем, но доказательства их не оставил. Часто он умышленно посылал теоремы своим знакомым без доказательства, тем самым предлагая им трудную задачу для решения. Современники часто с ними не справлялись, но в течение XVIII и XIX вв. все эти теоремы были доказаны. Все, кроме двух! Одна из них - только одна из всего богатого наследия Ферма - оказалась неверной^*: один раз и этому гению изменило математическое чутьё. А вторую, ту, которая была написана на полях Диофанта и о которой мы сейчас говорили, до сих пор не удалось ни доказать, ни опровергнуть.

^* (О ней будет сказано дальше, см. стр. 129.)

Лучшие математики пробовали на ней свои силы. Эйлер дал доказательства того, что уравнения х³+y³ = z³ и х⁴+y⁴ = z⁴ не разрешимы в целых числах, т. е. доказал теорему Ферма" для n = 3 и n = 4^*. Лежандр и Дирихле доказали её для n = 5, Ламэ - для n = 7. В середине прошлого века Куммеру с помощью трудной и тонкой теории удалось показать, что теорема Ферма может быть неверна лишь для некоторых исключительных значений n. Так, например, он доказал, что она верна для всех n, меньших 100^**. Но полного доказательства её справедливости он всё же не дал.

^* (Доказательство теоремы для n = 4 дал, по существу, сам Ферма.)

^** (В настоящее время она доказана для всех n, меньших 619 (и для ряда больших значений).)

Теорема эта сама по себе не имеет большого принципиального значения. Но она породила огромную литературу, привела к открытию новых теорий и методов решения задач и вообще сыграла такую роль в развитии математики, что ей присвоили наименование Великой теоремы Ферма.