Глава VI. Общая мера

Сложение и умножение - два прямых действия - обладают следующим важным свойством: эти действия всегда выполнимы в целых числах. Точнее говоря - если даны два любых натуральных числа, то всегда можно найти натуральное число, равное их сумме, и натуральное число, равное их произведению. Иначе обстоит дело в случае двух обратных действий: вычитания и деления. Не всегда можно найти натуральное число, равное разности двух данных натуральных чисел (например, не существует натурального числа, равного 5 - 8 или 6 - 6). Точно так же, не всегда удаётся найти натуральное число, равное частному двух натуральных чисел (например, не существует натурального числа, равного 5:8). Но между вычитанием и делением есть существенная разница. Узнать, вычитается ли одно натуральное число из другого, очень просто. Существует один единственный универсальный "признак вычитаемое": если число b больше числа а или равно ему, то из a нельзя вычесть b, т. е. нельзя найти натурального числа, равного (а - b). Наоборот, при делении часто бывает нелегко узнать, делится ли - число a на b или нет (т. е., будет частное ^a/_b натуральным числом или нет).

Число и наука о нем

Но этого мало. Из любого натурального числа, кроме единицы, можно вычитать некоторые другие натуральные числа (именно -все числа, меньшие его). При этом различных возможных вычитаемых у числа N будет всегда ровно N-1 (например, для числа 5 "возможными вычитаемыми" будут числа 1, 2, 3, 4, т. е. всего N - 1 = 5 -1 = 4 числа). В случае же деления дело обстоит гораздо сложнее. Существует число, имеющее только один делитель,- это единица; существуют числа, имеющие два делителя: единицу и самого себя: таковы числа 2, 3, 5, 7 и другие. Наконец, существуют числа, имеющие больше двух делителей: так, например, число 6 имеет четыре делителя (1, 2, 3 и 6). Числа, имеющие ровно два делителя, обладают многими замечательными свойствами. Их называют простыми или первоначальными числами.

Таким образом, уже самый поверхностный обзор арифметических действий над натуральными числами выдвигает две задачи, которые кажутся очень привлекательными, потому что на вид они очень просты. Первая из них - найти признаки ("признаки делимости"), позволяющие узнать, делится ли одно число на другое (так, чтобы в частном получилось натуральное число). Вторая задача - изучить свойства простых чисел. Обе задачи,- особенно вторая, значительно труднее, чем это кажется с первого взгляда. При изучении этих задач математики столкнулись с многими новыми вопросами. Некоторые из этих вопросов не решены и по сей день, хотя простыми числами математики занимаются уже больше двух тысяч лет. Признаки делимости и учение о простых числах составляют основной предмет учения о делимости - очень важной главы той Теории Чисел, о которой говорилось во введении к этой книжке.

Для того чтобы хоть немного познакомиться с некоторыми вопросами Теории Чисел, нужно вспомнить и продумать ряд основных определений и теорем из школьного курса арифметики.

Если существует натуральное число n, равное частному от деления числа a на b, т. е. такое, которое при умножении на b даёт a, то говорят, что a кратно b или что a делится на b. Число b называют делителем числа a. Так, например, 6 кратно двум; 15 делится на 5 и т. д. Тот факт, что b является делителем a, записывают в виде формулы следующим образом:

В учении о делимости приходится постоянно пользоваться тремя теоремами арифметики, которые представляют собою, так сказать, "разменную монету" большинства дальнейших рассуждений. Мы остановимся здесь на них, хотя это, быть может, и скучно, для того, чтобы в последующих главах они не отвлекали нашего внимания от сути дела. Вот эти теоремы:

Теорема 1. Если a делится на b, а b, в свою очередь, делится на c, то a делится на c.

Теорема 2. Если алгебраическая сумма (т. е. сумма или разность) нескольких чисел равна нулю или делится на число N, и все слагаемые, кроме одного, о котором ничего неизвестно, кратны N, то и это слагаемое тоже делится на N.

Теорема 3. Если произведение двух целых чисел a и b делится на число m, не имеющее с a общих делителей (кроме единицы, разумеется), то b делится на m.

Первые две теоремы совершенно ясны. Если 36 делится на 9, а 9, в свою очередь, делится на 3, значит, и 36 должно разделиться на 3. Точно так же, если 3 - x - 9 + 81 = 0, то ясно, что x должен быть кратным трём. Доказывать эти теоремы нужно не для того, чтобы убедить кого-то в их справедливости, а для того, чтобы показать их связь с ещё более простыми предложениями. Читатель докажет их без труда. Что касается третьей теоремы, то она, несмотря на кажущуюся простоту, доказывается более сложно. Мы к ней ещё вернёмся (на стр. 68-69).

Прежде чем итти дальше, задержимся немного на делении с остатком. Если умножение на целое число можно рассматривать как повторное сложение, то деление естественно рассматривать как повторное вычитание. Чтобы разделить, например, 20 на 5, будем вычитать 5 из 20: после первого вычитания получим 15, после второго - 10, после третьего - 5, после четвёртого получим нуль (при рассмотрении вопросов делимости удобно к натуральным числам присоединить число нуль, рассматривая, таким образом, все целые неотрицательные числа). Итак, здесь возможно четыре последовательных вычитания; это и значит, что частным от деления 20 на 5 является число 4; кому приходилось считать на счётах или на арифмометре, тому этот взгляд на деление покажется особенно естественным. Нетрудно сообразить, что количество повторных вычитаний равно числу, которое при умножении на делитель (т. е. на повторное вычитаемое) даёт делимое (исходное число).

Поскольку в этой и ближайших главах наряду с натуральными числами будет рассматриваться число нуль, нужно сказать несколько слов о свойствах этого, в некоторых отношениях исключительного, числа. Никакое число нельзя делить на 0. Действительно, чему может быть равно a:0 при а ≠ 0? Никакому числу такое частное равняться не может; ведь всякое число, умноженное на нуль, даст 0, а не a. Если же мы нуль попробуем делить на нуль, то в качестве частного сможем взять любое число, ибо любое число при умножении на О даёт 0. Ввиду этих обстоятельств в математике делить на нуль "строго воспрещается". Напротив, сам нуль можно делить на какое угодно число (неравное нулю), причём частным всегда будет нуль. Говоря о делении целых, но не обязательно натуральных чисел, мы приходим к выводу, что нуль делится на любое неравное нулю целое число без остатка, потому что 0:а=0, а нуль считается целым числом. На этом основании принято говорить, что нуль есть кратное любого числа.

Повторное вычитание оказывается применимым и тогда, когда делимое не является кратным делителя^*. В этом случае последнее вычитание приведёт не к нулю, а к некоторому числу, меньшему делителя,- к так называемому остатку. Будем, например, делить 17 на 5 способом последовательного вычитания. Вычитаем 5 из 17 первый раз - получаем 12, вычитаем второй раз - получаем 7, вычитаем третий раз - получаем 2. Дальше вы читать невозможно. Значит, частным от деления 17 на 5 будет 3 (число последовательных вычитаний), а в остатке получится число 2.

^* (Слово "делитель" имеет в арифметике два значения. Во-первых, делителем называют число, на которое делят другое число. Когда мы пишем a:b, то b называем делителем, даже если не знаем, что a должно разделиться на него (т. е. и в том случае, когда a:b не есть целое). С другой стороны, всякое число, кратное которого равно a, мы называем делителем а даже и в том случае, когда непосредственно о делении нет речи. В последнем случае вместо слова "делитель" употребляют иногда слово "множитель". Например, выражения: "разложить данное число на простые множители" и "найти все простые, делители данного числа" - значат по существу одно и то же. Эта двусмысленность при внимательном отношении к делу никогда не ведёт к путанице.)

Последовательное вычитание числа b из числа a, при котором получается частное n и остаток r, можно "перевести на язык формул", записав его так:

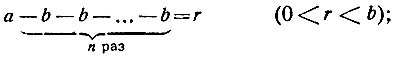
приведение подобных членов даёт: a-bn = r или а - r = bn, что формулируется следующим образом: если из числа а, которое при делении на b даёт остаток r, вычесть этот остаток, то разность a - r будет делиться на b. Более важно такое расположение членов в нашей формуле:

Это - основная формула, определяющая деление с остатком. При этом существенно, что r меньше b. Если r равняется нулю, то деление выполняется нацело. Чтобы не исключать и этого случая, мы в нашу последнюю формулу подставим и знак равенства (r = 0), присоединив его к знаку неравенства. Формула будет выглядеть так:

Из хода рассуждений ясно, что числа n и r определяются по числам а и b единственным образом. Иными словами, если даны два числа а и b, причём а>b, то единственным образом определяются частное n и остаток r; остаток этот неотрицателен (т. е. положителен или равен нулю) и всегда меньше делителя.

Оставим теперь современные учебники арифметики и посмотрим, как две с лишним тысячи лет назад подходил к вопросу о делимости один из крупнейших греческих математиков -Евклид. В своём сочинении "Начала", состоящем из 13 частей ("книг"), он подвёл итог математическим знаниям того времени и систематизировал их. "Начала" Евклида были так хорошо разработаны, что до самого недавнего времени, всего 100 лет назад, в школах Англии геометрию изучали прямо по книге Евклида, как по учебнику. В основном "Начала" были посвящены именно геометрии, но в них рассматривались и арифметические вопросы: пятая книга была посвящена теории пропорций, десятая - классификации иррациональных величин, а седьмая, восьмая и девятая арифметике целых чисел. В "Началах", между прочим, рассматривается разыскание общей меры двух отрезков и родственное ему разыскание общего наибольшего делителя двух целых чисел. Тот приём нахождения общего наибольшего делителя двух чисел, которым мы пользуемся в настоящее время, так и называется алгоритмом Евклида^*.

^* (Алгоритмом называется правило, которое позволяет автоматически решать какой-нибудь математический вопрос, выполнять определённое вычисление и т. д.)

Общею мерой двух отрезков называют такой третий отрезок, который на каждом из данных укладывается целое число раз. Найдём, например, общую меру отрезков АВ и CD на рис. 5. Отложим меньший отрезок CD на большем АВ от точки А столько раз, сколько окажется возможным. Если CD уложится некоторое число раз без остатка, то он, очевидно, и будет общею мерой. Если же, как на нашем рисунке, останется некоторый остаток D₃B, то придётся искать общую меру меньшего из данных отрезков (CD) и остатка (D₃B), т. е. на CD откладывать от точки С один за другим отрезки, равные D₃B. На рис. 5 отрезок D₃B откладывается на CD ровно четыре раза. Сам отрезок CD укладывается на АВ три раза с остатком, равным D₃B. Значит, D₃B укладывается на АВ ровно 4*3+1 = 13 раз. Итак, D₃B укладывается целое число раз и на АВ (13 раз), и на CD (4 раза). Он и есть общая мера этих отрезков.

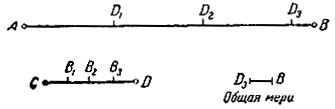
Рис. 5

Не всегда разыскание общей меры проходит так быстро и так гладко. Может случиться, что остаток не уложится целое число раз на меньшем отрезке. Тогда получится некоторый новый отрезок,- второй остаток,- который придётся откладывать вдоль первого остатка. Если какой-нибудь из остатков - пятый, десятый, сотый, тысячный... уложится целое число раз на предыдущем, то он и будет общею мерой двух исходных отрезков.

Может случиться и хуже. Может оказаться, что такое последовательное откладывание очередного остатка на предыдущем никогда не кончится. Каждый раз будет получаться новый остаток. В этом случае общей меры у данных отрезков найти нельзя; её не существует. Так, например, известно, что сторона квадрата и его диагональ не имеют общей меры.

В арифметике целых чисел тоже можно поставить вопрос об общей мере двух чисел, т. е, о таком числе, которое в каждом из данных "помещается" целое число раз, т. е. на него делятся без остатка оба данных числа. В отличие от отрезков, такая общая мера у целых чисел всегда существует: именно число 1, которое "укладывается" целое число раз в любом целом числе. Но, кроме единицы, пара чисел может иметь и другие "общие меры". Например, 6 и 20 имеют "общею мерой" число 2: оба они делятся на два.

Вообще, любое число, на которое делятся без остатка оба данных числа, служит их общею мерой. Поэтому, естественно, возникает вопрос обо всех общих делителях двух данных чисел и, в частности, об их общем наибольшем делителе.

Общим наибольшим делителем двух данных чисел называется наибольшее число, на которое делятся оба этих числа. Если общий наибольший делитель двух чисел равен единице, то числа эти называются взаимно-простыми. Например, 8 и 9 - числа взаимно-простые. Точно так же взаимно-простыми будут числа 12 и 35. Вот как определяет взаимно-простые числа сам Евклид: "Если из двух неравных целых чисел последовательно меньшее вычитается из большего и остаток до тех пор не измеряет точно предыдущего, пока он не равен единице, то данные числа суть числа между собою взаимно-простые".

Этот отрывок очень содержателен. Он не только даёт определение взаимно-простых чисел, но и показывает, как вычислять общий наибольший делитель. Поэтому, как мы уже говорили, приём вычисления общего наибольшего делителя называется алгоритмом Евклида.

Переведём на современный математический язык и разберём внимательнее эту чрезвычайно сжатую формулировку Евклида.

Пусть даны два натуральных числа а и b, из которых а больше b; требуется найти их общий наибольший делитель. По Евклиду, нужно из большего вычитать меньшее до тех пор, пока не получится остаток; вместо этого мы просто разделим а на b; при этом получится некоторое частное m₁ и некоторый остаток r₁, что мы можем записать так:

Остаток r₁ меньше чем b. Может случиться, что b точно разделится на этот остаток. Тогда правая часть написанного равенства, как сумма двух чисел, делящихся на r₁ сама будет делиться на r₁, а значит, и равное ей число а тоже разделится на r₁. Остаток r₁ будет общим делителем чисел а и b. С другой стороны, переписав наше равенство так: r₁ = а - bm₁} мы видим, что всякий делитель чисел а и b будет делителем числа r₁; следовательно, этот делитель будет не больше r₁, а это как раз и значит, что r₁ будет общим наибольшим делителем чисел а и b.

Пусть, например, a = 24, b = 16. Поделив 24 на 16, получим в частном 1 (m₁ = 1), а в остатке 8 (r₁ = 8). Но 8 есть делитель 16. Значит, 8 и будет общим наибольшим делителем чисел 16 и 24. Действительно, проверим это. Вот все делители чисел 16 и 24:

Наибольшим из общих делителей чисел 16 и 24 является, как мы и нашли, число 8.

Но может случиться, что меньшее из данных чисел не делится на r₁. Прежде чем разобрать этот случай, обратим внимание на одно важное обстоятельство. Долетим, что а при делении на b даёт остаток r₁. Мы уже видели, что на математическом языке этот факт записывается так:

Любой делитель чисел а и b будет делителем r₁, или иными словами, любой общий делитель пары а и b будет в то же время делителем пары b и r₁, следовательно, общий наибольший делитель чисел а и b будет в то же время общим наибольшим делителем чисел b и r₁. Мы получаем следующую теорему.

Теорема. Общий наибольший делитель двух чисел равен общему наибольшему делителю меньшего числа и остатка, полученного при делении большего из данных чисел на меньшее.

Вооружённые этой теоремой, вернёмся к рассмотрению того случая, когда при делении а на b получается остаток r₁, на который b точно не разделится. Тогда придётся при делении b на r₁ найти второе частное m₂ и второй остаток r₂. Именно это и имеет в виду Евклид, когда говорит о последовательном применении повторного вычитания (по-нашему: деления с остатком). Значит, получатся уже два равенства:

При этом новый остаток r₂ будет меньше нового делителя, т. е. первого остатка r₁. Таким образом, получается важный результат: r₂<r₁.

Будем применять этот приём последовательно, как нам советует Евклид. Разделим r₁ на r₂. Получим новое очередное частное m₃ и новый остаток r₃, который обязан быть меньше чем r₂:

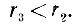
Спрашивается, окончится ли когда-нибудь этот ряд последовательных действий, или же возможно бесконечное повторение их, как это случается иногда при нахождении общей меры двух отрезков? Легко сообразить, что такое бесконечное повторение ряда действий в данном случае невозможно.

В самом деле, мы видели, что первый остаток r₁ меньше числа b. Второй остаток r₂ меньше r₁ и так далее:

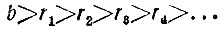
Все эти числа - b, r₁, r₂, r₃,...- целые и положительные, и каждое из них по крайней мере на единицу меньше предшествующего, так что они все различны. Но различных целых положительных чисел, меньших b, существует не так уже много: всего b-1. Следовательно, рано или поздно наши деления с остатком закончатся, и последнее деление будет уже без остатка.

Обозначим число последовательных делений с остатком буквою n:

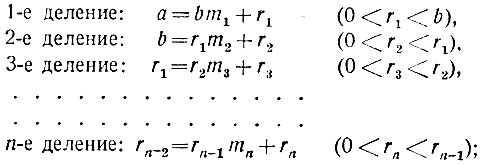
следующее, "эн плюс первое" деление непременно будет выполняться нацело:

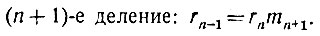
Теперь ко всем полученным равенствам применим только что найденную теорему об общем наибольшем делителе (стр. 64). Из первого равенства мы видим, что общий наибольший делитель чисел а и b равен общему наибольшему делителю чисел b и r₁. Но этот общий наибольший делитель равен, в силу второго равенства, общему наибольшему делителю чисел r₁ и r₂. Итак, общий наибольший делитель чисел а и b равен общему наибольшему делителю чисел r₁ и r₂. Рассмотрев третье равенство, убедимся, что он равен общему наибольшему делителю чисел r₂ и r₃. Дойдя последовательно до n-го равенства, убедимся, что общий наибольший делитель чисел а и b равен общему наибольшему делителю чисел r_n-1 и r_n. Но r_n-1, как мы видели, делится без остатка на r_1=n. Значит, r_n является общим наибольшим делителем чисел r_n-1 и r_n, и, следовательно, общим наибольшим Делителем чисел а и b. Значит, евклидов алгоритм, Действительно, ведёт к цели.

Как расположить действия при практическом вычислении общего наибольшего делителя, видно из следующего примера. Найдём общий наибольший делитель чисел а = 729 и b = 522.

Начинаем действие ближе к правому краю листа:

В этом примере выполнять деления приходится n+1 = 5 раз. Четвёртый остаток (r₄ = 9) и есть общий наибольший делитель чисел 729 и 522.

При нахождении общего наибольшего делителя двух чисел мы, выполняя последовательное деление, обращаем внимание только на остатки при отдельных операциях деления. Частные нас не интересуют. Поэтому-то остатки в предыдущем примере и напечатаны жирным шрифтом. Но в некоторых вопросах бывают важны последовательные частные; мы эти вопросы рассматривать здесь не будем^*.

^* (Последовательные частные нужны, например, при разложении данного числа в непрерывную дробь, где тоже применяется алгоритм Евклида.)

Вернёмся к столбику равенств, с которыми мы имели дело при разыскании общего наибольшего делителя. Вот этот столбик:

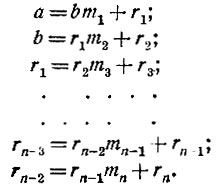
Здесь а и b - два данных числа (а больше чем b), m₁, m₂ и т. д. - последовательные частные, r₁, r₂ и т. д.- последовательные остатки.

Перепишем этот столбик "шиворот-навыворот", т. е. начиная с последнего равенства, причём каждое из равенств напишем в немного изменённой форме, решив его относительно крайнего правого члена. Получим столбик:

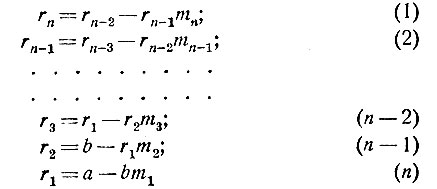
(все равенства мы перенумеровали). Подставим теперь в равенство (1) выражение для r_n-1 из равенства (2); мы получим:

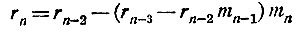
или

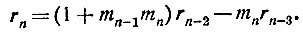
Последний остаток r_n, являющийся общим наибольшим делителем чисел а и b, выражается через числа r_n-2 и r_n-3, причём коэффициентами при r_n-2 и r_n-3 в этом выражении являются целые числа (положительные или отрицательные). Обозначим эти числа через А₁ и В₁:

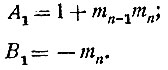
Тогда последнее равенство запишется так:

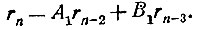
Перейдём теперь к равенству (3) нашего столбика (оно фактически не написано и заменено точками, но читатель без труда восстановит его). Это равенство выражает r_n-2 через r_n-3 и r_n-4. Подставляя его в выражение для r_n и делая приведение подобных членов, мы получим:

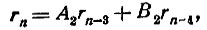
где А₂ и В₂ - опять некоторые целые числа (положительные или отрицательные). Повторяя эту операцию n раз, мы дойдём, наконец, до соотношения

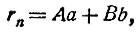
т. е. выразим общий наибольший делитель r_n двух любых целых чисел а и b через эти числа в виде суммы этих чисел, предварительно умноженных на некоторые целые коэффициенты A и В.

Это выражение (*) для общего наибольшего делителя двух целых чисел играет очень важную роль в Теории Чисел, и мы в этой книжке ещё не один раз с ним встретимся.

Вот первое применение равенства (*).

Рассмотрим два взаимно-простых числа а и m (т. е. таких, что их общий наибольший делитель равен единице). Предположим, что произведение ab данного числа а и некоторого целого числа b делится на m. Что можно сказать о делимости b на m?

Применим только что разобранное свойство общего наибольшего делителя двух чисел, который выражается через эти числа по формуле (*), причём коэффициентами разложения будут целые (положительные или отрицательные) числа. Следовательно, равенство (*) перепишется так:

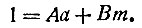
(r_n в нашем случае равен единице, потому что a и m - взаимно-простые!)

Умножив обе части последнего равенства на b, получим:

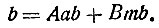
Оба члена правой части делятся на m: первый - потому что ab делится на m по условию, а второй - содержит множитель m явно. Следовательно, и левая часть, т. е. число b, разделится на m.

Мы получили доказательство теоремы третьей, о которой говорилось в начале этой главы (стр. 58).

С последовательным делением - правда, несколько иного рода - мы уже встречались при переводе числа из одной системы счисления в другую (стр. 40). Там, в отличие от евклидовского алгоритма, все делители были одинаковы. Остановимся на этом делении несколько подробнее.

Предположим, что нам дано какое-нибудь число а и основание системы счисления m. Само число а может быть задано в какой-либо иной системе счисления, записано римскими цифрами или дано ещё как-нибудь иначе. Возникает принципиальный вопрос: можно ли число а записать в позиционной системе с основанием m? Как это делать практически, мы знаем; все примеры, с которыми приходилось сталкиваться в главах IV и V, как будто подтверждают такую возможность. Остаётся рассмотреть вопрос с общей, теоретической точки зрения - доказать теорему в общем виде.

Итак, нужно число a записать в системе с основанием m. Делим а на m. В результате, как мы знаем, единственным образом определятся частное n₁ и остаток r₁:

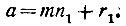
Частное n₁ показывает, сколько в числе а содержится групп по m единиц, т. е. единиц второго разряда. Остаток r₁ даёт число свободных единиц первого разряда. Если число n₁ меньше основания системы счисления, то задача решена: наше число состоит из n₁ единиц второго и r₁ единиц первого разряда и запишется так:

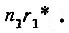
^* (Здесь, как и в главе IV (см. стр. 41), n₁r₁ обозначает не произведение чисел n₁ и r₁, а просто две рядом написанные цифры, так, например, цифры 3 и 5 в числе 35.)

Если же n₁ более m, то повторяем ту же операцию: Делим n₁ на m и получаем в частном какое-то число n₂ и в остатке r₂. Частное показывает число единиц третьего разряда, а остаток - число единиц второго. Если n₂ меньше m, то задача решена: искомая запись числа а в системе с основанием m будет выглядеть так:

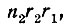
(т. е. n₂m² + r₂m + r₁). Если же n₂ больше чем m, то снова повторяем деление.

Но число а - данное, вполне определённое. Если мы рассмотрим ряд степеней целого числа m, большего единицы, именно: m, m₁, m₂, m₃,..., то в этом ряду обязательно найдётся степень с таким показателем - назовём его q,- что m^q будет больше чем а. Значит, после q последовательных делений на m наши деления закончатся, и мы получим единственное, вполне определённое представление числа а в позиционной системе с основанием m. Это мы и хотели доказать.