Глава V. Арифметика, в которой не нужно считать

Система счисления, в основание которой положено число "два", обладает многими замечательными свойствами. Она заслуживает того, чтобы на ней задержаться. В ней используются только два знака для записи чисел: знак для единицы (1) и позиционная пробка - нуль (0).

Число и наука о нем

В этой главе, как и в предыдущей, числа, изображённые по двоичной системе, будут напечатаны жирным шрифтом, а числа, записанные по десятичной - обыкновенным.

Для единицы мы имеем знак 1. Число "два", будучи основанием системы счисления, станет единицей второго разряда и запишется так: 10. Число "три", состоящее из единицы второго разряда (два) и простой единицы, запишется так: 11. "Четыре" является квадратом двух, т. е. единицей третьего разряда, поэтому оно запишется так: 100. Что касается числа восемь, равного двум в кубе, то его придётся записать, как нашу тысячу: 1000.

Мы видим, что наши однозначные числа оказываются в двоичной арифметике трёх-и даже четырёхзначными. В дальнейшем мы увидим, что запись действий тоже занимает значительно больше места, чем наша. Всё это делает двоичную систему практически мало пригодной. Но простота выполнения действий в этой системе поистине изумительна.

Начнём со сложения. Сложим, например, 10110 и 1101 (т. е. 22 и 13).

Подпишем эти числа одно под другим, как при обычной записи:

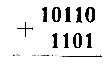
Если в каком-либо столбике имеется одна единица (вторая цифра - нуль), то пишем её под чертой. Если же имеются две единицы, как в третьем столбике, то зачёркиваем их, внизу ставим нуль, а сверху, над следующим разрядом, приписываем единицу. Далее делаем то же со следующим разрядом, учитывая и надписанные сверху единицы. Всё действие выглядит так:

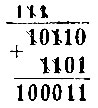
По существу делается то же, что и в обычной записи, но считать совершенно не приходится: ставятся только палочки да нулики, и палочки перекрещиваются. Вот более сложный пример (справа он же записан в десятичной системе счисления):

Зачеркнув две единицы в крайнем правом столбце, мы ставим сверху над вторым столбцом (над чертой) добавочную единицу; зачеркнув ещё две единицы, ставим ещё добавочную единицу. Больше единиц в правом столбце нет. Поэтому под чертой пишем нуль. То же случится со вторым столбцом справа; при этом нужно Учитывать и единицы, стоящие над верхней чертой. В третьем столбце (справа) имеются три единицы; две из них мы зачеркнём, поставив единицу над четвёртым столбцом, а третью снесём под нижнюю черту, и так далее.

Запись, сравнительно с нашей десятичной, очень громоздка. Но выполняется действие автоматически. Пятилетнего ребёнка можно быстро этому научить.

Вычитание производится проще всего, если пользоваться "правилом дополнения". Десятичным дополнением данного числа называется разность между ближайшей большей степенью десяти ("единицей с нулями") и данным числом. Так, например, десятичным дополнением числа 7 будет 3, числа 89 - число 11, для числа 6385 десятичным дополнением будет 3615, для числа 580 - число 420. Чтобы найти дополнение, нужно все цифры данного числа вычесть из девяток, последнюю (не считая нулей на конце) - из десяти. Теперь нетрудно заменить вычитание сложением: вместо того, чтобы вычитать какое-либо число из данного, достаточно прибавить к последнему десятичное дополнение вычитаемого и вычесть степень десяти. Например, вычитая 5833 из 11021, расположим действие так:

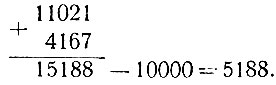
Подобно десятичному дополнению вводится и двоичное дополнение. Двоичным дополнением данного числа называют разность между ближайшей степенью двух и данным числом. Находить двоичное дополнение числа, записанного по двоичной системе счисления, ещё проще, чем находить дополнение десятичное. Пусть, например, нужно найти двоичное дополнение числа 11010111000. Последнюю правую единицу и все следующие за ней нули (если они есть) оставляем без изменений, а во всём остальном - заменяем единицы нулями, а нули - единицами. Если в результате получаются нули спереди, то их просто зачёркиваем - вплоть до первой единицы. Так, из числа 11010111000 получается число

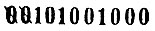
т. е. 101 001 000. Это и есть двоичное дополнение числа 11010111000.

Умея находить двоичные дополнения, мы сумеем автоматически выполнять вычитание. Вычтем, например, 11011 из 1110001.

Находим двоичное дополнение вычитаемого. Получим

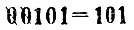
Заменяем теперь вычитание сложением:

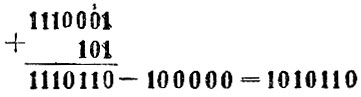
В десятичной системе запись вычитания этих же чисел будет короче: 113 - 27 = 86.

При сложении и вычитании чисел, данных в двоичной системе, громоздкая запись совершенно обесценивает ту автоматичность, которой отличается выполнение действий. Но при умножении эта автоматичность бросается в глаза, и громоздкая запись не маскирует необычайной простоты самого действия.

Таблица умножения в двоичной системе счисления имеет следующий вид:

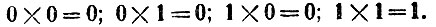
Запись действия располагаем так же, как и при обычной записи.

Перемножим, например, числа 111 001101 и 1101 101.

(Под множителем при двоичном умножении мы пишем две черты, чтобы оставить между ними место для единиц, которые получатся в результате сложения и которые при обычном умножении мы держали бы в уме.)

Десятичная запись гораздо короче (она дана рядом с двоичной, справа). Но выполнение десятичного умножения многозначных чисел требует известной квалификации. Нужны годы работы, чтобы научить ребёнка безошибочно выполнять такое умножение. Между тем, двоичное умножение выполняется совершенно автоматически.

Самым трудным из арифметических действий является, несомненно, деление. Всякий помнит, вероятно, каким сложным ему казалось деление в детстве. Да и взрослый человек вряд ли испытает особое удовольствие, деля, например, 8 663 545 198 на 87 995. В средние века деление считалось столь трудной операцией, что людям, искусным в этом действии, давалась учёная степень.

А в двоичной системе счисления и деление выполняется совершенно автоматически! Правда, простота и автоматичность покупаются здесь ценою чрезвычайно громоздкой записи. В качестве примера разделим 11011101 на 10 111. Действие располагаем так же, как при обычном делении, но каждый раз под делимым будем подписывать не произведение делителя на соответствующую цифру частного, а двоичное дополнение этого произведения (при этом нули спереди можно и не зачёркивать).

В частном получается 1001 и в остатке 1110. Справа дано выполнение деления этих же чисел в обычной (десятичной) записи. Сразу видно, что двоичная система практически неприменима потому, что запись очень громоздка. Но что-то считать, что-то пробовать, что-то замечать - здесь совершенно не приходится.

На необычайную простоту и своеобразие двоичной системы счисления первый из европейцев обратил внимание знаменитый философ и математик Г. В. Лейбниц (1646-1716). Но китайцам она, повидимому, была известна значительно раньше.

Двоичная система счисления имеет разнообразные применения в различных отделах математики. Рассказать о них в этой книжке, рассчитанной на читателя без специальной подготовки, очень трудно. Вместо этого мы дадим несколько задач, в которых особенности этой системы выступают очень ярко.

Большинство применений двоичной системы основано на следующем её свойстве: во всех остальных системах счисления нужно указывать, сколько единиц каждого разряда входит в состав данного числа (например, называя или записывая число девятьсот пятьдесят один, мы отмечаем, что оно содержит девять сотен, пять десятков и одну единицу); в двоичной же системе единица любого разряда может либо присутствовать (тогда непременно в единственном числе), либо отсутствовать. Нет надобности говорить, что в двоичном разложении некоторого числа имеется столько-то единиц третьего разряда, столько-то второго, столько-то первого. Достаточно сказать: есть единица третьего разряда, нет - второго, есть - первого. Этим число вполне определено: в рассмотренном примере мы имеем число 101 = 5. Чему, например, равно число, в котором есть единица десятого разряда, нет - ни девятого, ни восьмого, ни седьмого, есть - шестого и пятого, нет - четвёртого и всех низших? Ответ получается сразу: это будет число 1000110 000, т. е. 560.

Всё это можно выразить иначе. Рассмотрим ряд чисел, начинающийся с единицы, из которых каждое в два Раза больше предыдущего (геометрическую прогрессию):

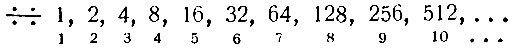
Любое число может быть представлено в виде суммы нескольких членов этого ряда. Например, 19 равно сумме первого, второго и пятого чисел ряда (нумера членов проставлены под ними); сто равно сумме третьего, шестого и седьмого членов и т. д. Действительно, всякое число можно записать в двоичной системе счисления: тогда единицы укажут на присутствующие, а нули - на отсутствующие члены этой прогрессии (19 = 10011, 100 = 1100100).

Теперь нетрудно объяснить следующий фокус с угадыванием числа. Вы предлагаете товарищу задумать какое-нибудь число от 1 до 31, затем даёте ему картонную табличку, изображённую на рисунке 4, и предлагаете, не показывая вам таблицу, сказать, в каких строчках имеется число. Как только он назовёт нумера строк, вы сейчас же называете задуманное число.

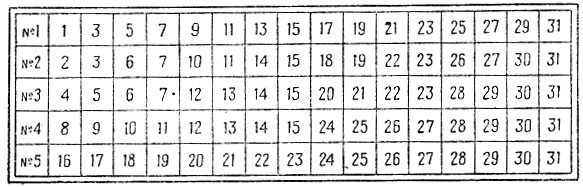
Рис. 4

Составлена эта таблица очень просто. В первой строке помещены все те числа (от 1 до 31), в двоичной записи которых на первом справа месте стоит единица (т. е. все нечётные числа). Во второй строке помещены те числа, в двоичном разложении которых на втором месте справа стоит единица. Число "три", например, которое в двоичной системе счисления записывается так: 11, помещено и в первую и во вторую строку, так как у него и первая справа и вторая цифра - единицы. Так же построены и остальные строки. В последней, пятой строке помещены все те числа (в пределах от 1 до 31), у которых на пятом месте двоичного разложения стоит единица, т. е. числа от 16 до 31.

Пусть, например, задумано число 29. Загадывающий видит это число в первой, третьей, четвёртой и пятой строках. Назвав вам эти строки, он тем самым невольно указывает, что в двоичное разложение задуманного числа входят единицы первого, третьего, четвёртого и пятого разрядов. Вы знаете, что единицами этих разрядов в двоичной системе счисления служат числа 1, 4, 8 и 16 (они выписаны в первом столбце каждой строки). Остаётся сложить их в уме, что и даст 29. Теперь легко восстановить почти мгновенно задуманное число: нужно только сложить в уме эти несколько небольших чисел.

Для выполнения следующего эффектного фокуса нужно научиться быстро запоминать несколько двузначных чисел (т. е. количество цифр, соответствующее двум телефонным нумерам; запомнить сразу два телефонных нумера нетрудно, тем более, что держать их в памяти придётся всего несколько минут). Фокус состоит в следующем. Вы предлагаете товарищу нарисовать квадратик из 5×5 клеток и расставить в его клетках произвольным образом крестики. Затем в течение полуминуты смотрите внимательно на квадрат и возвращаете его товарищу. Через пять минут вы берётесь нарисовать на память расположение крестиков, и это вам удаётся сразу. Окружающим кажется, что это очень просто, но предложите любому в течение полминуты запомнить расположение крестиков в квадрате: можете быть уверены, что никто этого не сможет сделать.

В чём же секрет быстрого запоминания расположения крестиков на квадратной таблице? Легче всего разобрать это на примере. Пусть вам дали следующее расположение крестиков:

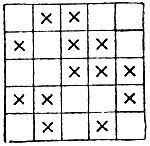
Считайте, что крестики это - единицы, а пустые клетки - нули. Тогда на каждую строку можно смотреть, как на число, записанное по двоичной системе. В нашем примере мы имеем следующие числа:

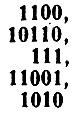
(нули, стоящие впереди единиц, пропущены). Прочитать эти числа легко, вот они:

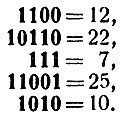
При некотором навыке этот перевод из двоичной системы в десятичную выполняется почти мгновенно. Остаётся запомнить серию чисел: 12 - 22 - 07 - 25 - 10. На перевод из двоичной системы в десятичную и на запоминание этой серии достаточно после небольшой тренировки полуминуты.

Через пять минут, когда расположение крестов у всех исчезло из памяти, вы продолжаете помнить серии чисел: 12 - 22 - 07 и 25 - 10 (как бы два телефонных нумера). По этим числам можно сразу восстановить первоначальную таблицу: нужно только написать их одно под другим в двоичной системе счисления и заменить единицы крестиками.

Эта возможность использовать двоичную систему счисления в качестве приёма запоминания квадратных таблиц применяется в шифровальном деле и в конспиративном письме. Как это осуществляется, подробно рассказано в книге Я. И. Перельмана "Живая математика"^*.

^* (Гостехиздат, М.- Л., 1946 г.)

Внимательный читатель обратит внимание на то, что во всех наших рассуждениях есть одна нестрогость. Мы несколько раз употребляли выражение: "всякое число (целое) - можно записать в позиционной системе счисления с любым основанием". Верно ли это? Рассуждения, которыми мы пользовались в предыдущей главе, записывая одно и то же число при различных основаниях, показывают, что, повидимому,- верно. Более основательно этот вопрос будет разобран дальше, в конце главы VI (стр. 69); там возможность изображения любого числа в позиционной системе с любым основанием будет строго доказана.

В заключение заметим следующее. Как с помощью десятичной системы счисления можно записывать не только целые числа, но и дробные (десятичные дроби), точно так же можно ввести двоичные, троичные и т. д. дроби. Дроби эти имеют любопытные приложения, но эта книжка посвящена только целому числу и поэтому дробей мы касаться здесь не будем.