Глава IV. Не десятками, а пятками или дюжинами

При современном состоянии науки нельзя, повидимому, придумать систему счисления, которая была бы удобнее позиционной. Но в основу позиционной системы счисления можно ставить разные числа: у нас основой системы является число 10, у вавилонян было 60, у Архимеда - 10⁸. Эти системы, удобные для наименования чисел, очень неудобны для их записи: приходится вводить слишком, много знаков (цифр) для чисел первого разряда. Но может быть, позиционная система с основанием 3 или 15 оказалась бы удобнее нашей десятичной?

Число и наука о нем

Оказывается, что при решении различных задач могут оказаться удобными различные системы счисления. Возможно, что некоторые системы, например, двенадцатиричная, и в целом оказались бы несколько лучше десятичной. Но привычка считать десятками так велика, а обязательный переход к новой системе счисления вызвал бы такую ломку всех привычек и такие материальные расходы, что вряд ли подобную реформу можно было бы признать целесообразной.

Есть, впрочем, одна система счисления, настолько своеобразная, её преимущества перед десятичной в одних вопросах и недостатки в других так резко бросаются в глаза, что стоит её рассмотреть внимательно. Это - двоичная система, или система при основании 2. Ей будет посвящена следующая глава. А в этой главе поговорим о позиционных недесятичных системах вообще и научимся переходить от одной из таких систем к другой.

Кроме счёта десятками, в быту довольно широко распространён счёт пятками. В Китае принято считать пятками, причём пятки группируются в пары; получается своеобразная система счисления, в которой каждая единица чётного порядка в пять, а нечётного - в два раза больше предыдущей. Орудием счёта служат китайские счёты, которые не так давно можно было видеть и в Москве в китайских прачечных (рис. 3).

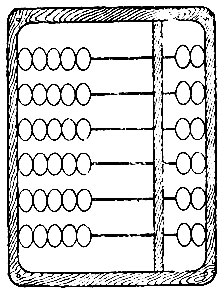
Рис. 3

Не задерживаясь далее на этой сложной системе счисления с двойным основанием, отражающей счёт с помощью двух рук, рассмотрим чистую пятиричную систему, т. е. позиционную систему с основанием пять. Эта система использует для записи всех чисел только пять знаков-цифр: знаки для чисел "один", "два", "три", "четыре" и позиционную пробку - знак для нуля. Для обозначения этих первых четырёх чисел и нуля можно воспользоваться хотя бы нашими цифрами: 1, 2, 3, 4, 0, но напечатанными жирным шрифтом.

Число "пять", являющееся одним "пятком", т. е. одной единицей второго разряда, придётся записать так: 10 (как наше "десять"), поставив на месте отсутствующих простых единиц нуль.

Запишем по пятиричной системе число 387 (триста восемьдесят семь; обычный, светлый шрифт указывает на обычную, десятичную запись). Прежде всего, выясним, сколько в нашем числе пятёрок (единиц второго разряда) и сколько простых единиц. Чтобы это узнать, поделим 387 на пять. Частное даст число пятёрок, остаток - число простых единиц:

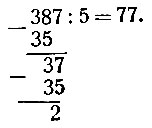
Итак, в нашем числе 2 простых единицы и 77 единиц второго разряда. Но каждые пять единиц второго разряда составляют единицу третьего разряда; очевидно, в семидесяти семи единицах второго разряда содержится некоторое количество единиц третьего разряда. Чтобы найти его, повторяем операцию деления: делим 77 на 5:

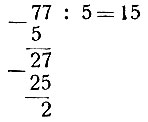
Остаток (2) даёт число единиц второго разряда, частное же - число единиц третьего. Ищем, сколько в пятнадцати единицах третьего разряда содержится единиц разряда четвёртого:

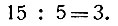
Пятнадцать единиц третьего разряда состоят целиком из единиц четвёртого разряда. Отсутствие остатка указывает, что "свободных" единиц третьего разряда нет. Что касается трёх единиц четвёртого разряда, то ясно, что в них содержаться единицы высших разрядов не могут. Значит, число 387 состоит из трёх единиц четвёртого разряда, не содержит вовсе единиц третьего разряда, содержит две единицы второго и две единицы первого разрядов, т. е. может быть записано так: 3022.

Все действия могут быть сгруппированы вместе:

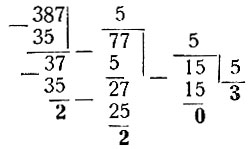
Напечатанные жирным шрифтом числа (остатки и последнее частное) нужно ещё переписать в обратном порядке.

Решим теперь обратную задачу. Пусть число дано в пятиричной системе: 2341. Найти его десятичное выражение.

Подумаем, что обозначает каждая из цифр этого числа. Стоящая справа единица обозначает просто 1. Стоящая на втором (справа) месте четвёрка обозначает четыре пятка, т. е. 4*5; следующая за ней тройка обозначает той "пять раз взятых пятка", т. е. 3*5²; наконец, крайняя левая двойка обозначает 2*5³. Следовательно,

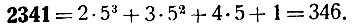
Заметим, что и написанное по десятичной системе число, например 3208, может быть дано в аналогичной форме: 3*10³ + 2*10² + 0*10 + 8. (В третьем слагаемом этого выражения (0*10) множитель "нуль" есть число целое, но не натуральное.)

Вообще, если в основание системы счисления положено число m, то abcdk^* обозначает:

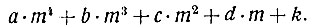
^* (Здесь, в отличие от принятой в алгебре записи, выражение abcdk обозначает не произведение чисел a, b, c, d и k, а число, записанное в некоторой позиционной системе счисления с помощью цифр a, b, c, d, k. )

В нашем быту остались кое-какие пережитки счёта дюжинами. Английский фут, как и русский дореволюционный, делится на 12 дюймов. Ряд товаров упаковывается в тару дюжинами, а для дюжины дюжин в торговле имеется специальное наименование - гросс. Надо сказать, что двенадцатиричная система счисления в некотором отношении лучше десятичной: двенадцать имеет четыре целых делителя (не считая 1 и самого числа 12): 2, 3, 4, 6, тогда как 10-только два (2 и 5). Поэтому при двенадцатиричной системе было бы больше "круглых" чисел, а это позволило бы установить больше сокращённых приёмов выполнения действий. Но в общем выигрыш был бы невелик.

Совсем недавно в Америке возникло добровольное общество, ставящее себе целью распространение, пропаганду и постепенный переход к двенадцатиричной системе счисления. Мы говорили уже, что в наше время такой переход нецелесообразен. А в недалёком будущем люди изобретут столь совершенные счётные машины, и эти машины будут так доступны, что вопрос о рациональной системе счисления либо потеряет актуальность, либо разрешится сам собой. Упомянутая американская ассоциация- просто забава досужих людей.

В двенадцатиричной системе счисления, кроме нуля и цифр от одного до девяти, пришлось бы ввести ещё цифры для обозначения десяти и одиннадцати. Обозначим условно эти цифры значками X и Л. Запишем, например, число 1443 по двенадцатиричной системе:

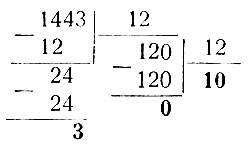
Последнее частное равно десяти, остатки: нуль и три. Следовательно, 1443 = Х03.

Во всех рассмотренных задачах указывались системы счисления и требовалось выразить заданные числа. Можно ставить и другие задачи. Например, по данной записи действий над числами установить, в какой системе счисления сделана запись. Вот пример такой задачи: дана запись

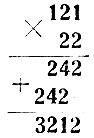
В какой системе счисления она справедлива?

Внимательно приглядываясь к выполнению действий, мы замечаем, что 2 + 4 дают какое-то число, оканчивающееся единицей^*. Но "два" и "четыре" дадут "шесть", как бы мы их ни записывали. Значит, знака для числа "шесть" в этой системе счисления нет. Но цифру 4 (четыре) мы в данной записи находим. Следовательно, система счисления может быть либо пятиричной, либо шестиричной. Записав число "шесть" в обеих этих системах, получим 11 (пятиричная) и 10 (шестиричная). Следовательно, в указанном примере, где 2 + 4 даёт число, оканчивающееся единицей, система счисления - пятиричная.

^* (Предполагается, что цифры обозначают те же числа, что и в нашей системе счисления, т. е. что 1 есть знак для единицы, 2 - для числа "два" и т. д.)

Вот ещё лёгкий пример: в какой системе счисления 3×3 = 10? Читатель сообразит, что это возможно только при основании девять.

Не всегда, однако, по виду действия можно однозначно установить, в какой системе счисления справедлива запись. Например, равенство 122×3 = 366 справедливо в любой системе счисления с основанием, большим шести.

Но случается и так, что по "жалким остаткам" какого-либо действия удаётся не только установить систему счисления, в которой произведена запись, но и восстановить действие. Вот пример: пусть известны лишь некоторые цифры действия (остальные заменены звёздочками):

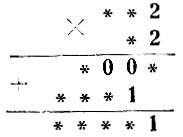
По какой системе счисления это написано? Как восстановить пропущенные цифры?

Смотрим прежде всего на последние цифры множимого и множителя и на последнюю цифру результата. Мы видим, что число "четыре" (дважды два) в этой системе счисления оканчивается единицей, т. е. для него нет специального знака. Это возможно только при основаниях, не превосходящих четырёх, т. е. при основаниях 2, 3 или 4. При основании "2" число "четыре" (квадрат основания) запишется так: 100; при основании "3" число "четыре" запишется так: 11 (т. е. 3*1 + 1). Наконец, при основании "4" число "четыре" (само основание) запишется так: 10. Значит, искомым основанием может быть только число "три". "Три" и будет ответом на первый вопрос задачи.

Обозначив далее вторую цифру множимого через х и учитывая единицу в уме, получим, что 2x+1 даёт число, оканчивающееся нулём; это возможно только при х=1^*. Точно так же найдём, что первая цифра множимого равна единице. Значит, множимое равно 112, т. е. числу "четырнадцать".

^* (х может равняться 0, или 1, или 2 (ведь система-то счисления-троичная). Но 2*0+1 = 1; 2*1+1 = 10; 2*2+1 = 12. Значит, х должен равняться 1.)

Левая цифра множителя при умножении на два даёт число, оканчивающееся единицей. Но 2*0 = 0; 2*1 = 2; 2*2 = 11. Значит, эта цифра может равняться только двум, множитель равен 22 (восемь) и всё действие запишется так;

Для проверки запишем 112 в троичной системе счисления:

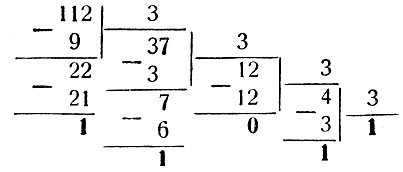
Получается как раз 11011.

Перейдём от примеров к общим выводам. Чем меньше основание системы счисления, тем, очевидно, более громоздкой становится запись чисел и действий над ними. Вот, например, как выглядит умножение двадцати трёх на семнадцать в десятичной и в троичной системах счисления:

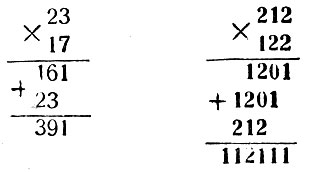
Запись в троичной системе занимает больше места, чем в десятичной, и является, следовательно, более громоздкой, то касается самого процесса письменного счета, то нетрудно видеть, что в троичной системе он гораздо проще, чем в десятичной.

Действительно, чтобы считать. "столбиками", как это обычно принято, нам приходится помнить наизусть "таблицу сложения" и "таблицу умножения". "Таблицу сложения" мы осваиваем в течение двух-трёх лет постепенно; с заучиванием таблицы умножения у всякого, вероятно, связаны не очень приятные воспоминания.

При маленьком основании и таблица сложения и таблица умножения значительно проще, чем у нас. Вот эти таблицы при основании "3":

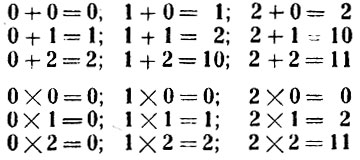
Ясно, что заучить эти таблицы значительно проще, чем наши.

Наименьшее натуральное число, которое может служить основанием системы счисления, есть "два". В этой системе действия должны выполняться особенно просто. В "следующей главе мы увидим, что это действительно так. При позиционной нумерации с основанием "два" почти все выкладки выполняются автоматически: получается своеобразная "арифметика, в которой не нужно считать".