Глава III. Для чего и как Архимед считал песок?

В III в. до н. э. на острове Сицилия жил математик совершенно исключительной одарённости. И сейчас, более чем через две тысячи лет после его кончины, имя его известно любому школьнику. Это был Архимед (рис. 2). Замечательный геометр, механик, физик и военный инженер, он оставил среди своих многочисленных творений удивительное сочинение по арифметике. Называется оно "Псаммит или исчисление песку в пространстве, равном шару неподвижных звёзд".

Рис. 2

Архимед впервые убедительно показал, что чисел бесконечно много, что для любого количества предметов, как бы велико оно ни было, можно найти соответствующее число; можно для любого числа указать его место в ряду уже известных чисел, построить числа ещё большие и назвать все эти числа. Иными словами, он построил научную систему счисления.

Число и наука о нем

В качестве примера он рассмотрел песок, который часто считается символом бесконечного множества (говорят - "бесчисленны, как песок морской"...). Он показал, что числом можно выразить не только весь песок на Земле. Если бы вся вселенная состояла сплошь из песка, то и тогда нашлось бы число, с помощью которого можно выразить такое количество песчинок. Для решения этой задачи он строит нумерацию, которую мы и разберём внимательно. Но сначала посмотрим, как Архимед представлял себе мир, и решим его задачу с помощью нынешних приёмов вычисления.

Архимед считал мир очень большим, но всё же ограниченным: именно, он считал его шаром, на поверхности которого расположены неподвижные звёзды, а внутри находятся Земля, Солнце и планеты. Радиус этого шара он считал в мириаду, т. е. в десять тысяч раз большим, чем расстояние от Земли до Солнца, а последнее полагал равным мириаде мириад стадий, т. е. по-нашему 150*10⁷ км*.

^* (Греческая стадия равнялась приблизительно 150 метрам. От слова "стадия" происходит "стадион" - первоначально - разделённая на стадии дорожка, на которой состязались бегуны. Слово "мириада" значит десять тысяч. Слов для обозначения чисел, больших чем 10 000, в греческом языке не было.)

Это - в десять раз больше среднего расстояния от Земли до Солнца, для которого современные измерения дают приблизительно 150*10⁶ км. Таким образом, радиус вселенной Архимеда, в пересчёте на наши меры, равнялся 15*10¹² км. Это, примерно, в три раза меньше фактического расстояния до ближайшей к нам звезды. Значит, радиус архимедовой вселенной в сто миллионов раз меньше, чем радиус мира, доступного нашим современным телескопам.

Теперь нетрудно вычислить объём архимедовой "сферы неподвижных звёзд". Он равен

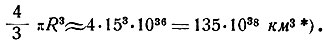
^*) (Мы считаем, для простоты расчётов, π = 3. Эта неточность не влияет на существо результата.)

Остаётся подсчитать, сколько в этот объём можно вместить песчинок. Архимед считал, что в объёме макового зерна может вместиться мириада (10 000) песчинок (иными словами, он рассматривал весьма тонкий песок - лёгкую пыль). Поперечник макового зерна он считал равным одной сороковой части дюйма^*, т. е. по-нашему ¹/₂ мм.

^* (Греческий дюйм равнялся приблизительно 2 см.)

Считая, для простоты, что зерно имеет форму кубика, мы видим, что в одном кубическом миллиметре содержится 8 маковых зёрен или 80 000 песчинок; в кубическом метре - в 10⁹ (в биллион) раз больше, т. е. 8*10¹³, а в кубическом километре - ещё в 10⁹ больше, т. е. 8*10¹³*10⁹ = 8*10²² песчинок. Остаётся перемножить число кубических километров архимедовой вселенной (135*10³⁸) и число песчинок в одном кубическом километре (8*10²²). Это даст, примерно, 10⁶³ песчинок - число и по нашим современным масштабам громадное.

Мы без труда решили архимедову задачу. Но во времена Архимеда не было названий для чисел, больших десяти тысяч, не было десятичной системы счисления, не было знака показателя, не было разработанных правил действий. Заслуга Архимеда именно в том, что он выдумал, как называть большие числа и как производить с ними вычисления (при вычислениях он пользовался только свойствами арифметической и геометрической прогрессий, которые и в то время были известны). Это вычисление очень интересно, но говорить о нём в нашей небольшой книжке нет возможности^*. Мы рассмотрим только архимедову систему счисления.

^* (Интересующиеся с удовольствием прочтут сами "Псаммит", который, начиная с 1824 г., неоднократно издавался в русском переводе. Последнее издание: "Исчисление песчинок", перевод Г. Н. Попова, М.- Л., 1932 г.)

Для первого десятка тысяч, т. е. до первой мириады, Архимед использует существовавшие тогда греческие числительные. Далее он называет числа до мириады мириад подобно тому, как мы называем числа до тысячи тысяч. Так число 85 643 911 Архимед назовёт: "восемь тысяч пятьсот шестьдесят четыре мириады три тысячи девятьсот одиннадцать". Все числа от единицы до мириады мириад он называет "числами первыми". Простую единицу он называет "единицей чисел первых", а мириаду мириад единиц чисел первых - "единицей чисел вторых". Итак, "единица чисел вторых" - это 10⁸. Теперь нетрудно назвать числа до мириады мириад "единиц чисел вторых", т. е. по-нашему до 10¹⁶. Это число Архимед называет "единицей чисел третьих" и т. д. Мы видим здесь позиционную систему счисления с основанием 10⁸, но разработаны только названия, а не написание чисел, в котором Архимед для решения своей задачи не нуждался. Единица каждого разряда у Архимеда в 10⁸ раз больше единицы предшествующего разряда.

Таким образом можно дойти до единицы любых чисел вплоть до мириадо-мириадных. Единица n-х чисел будет равна, как легко сообразить, 10^8(n-1) (например, единица десятых чисел - 10^8(10-1) = 10⁷²; единица сто двадцать четвёртых чисел - 10^8(124-1) = 10⁹⁸⁴ и т. д.). Счёт можно довести до мириады мириад чисел мириадо-мириадных, т. е. до 10⁸*10^{8(100000000-1)} = 10^8*108. Этих чисел Архимеду вполне достаточно для решения его задачи. Мы видели, в самом деле, что решением служит 10⁶³ = 10⁷*10^8(8-1), т. е. тысяча мириад единиц чисел восьмых.

Но Архимед на этом не останавливается. Как мы, кроме единиц различных разрядов, вводим единицы различных классов, так он вводит числа различных периодов. Все числа до 10^8*108 он называет числами первого периода. Мириаду мириад чисел мириадо-мириадных он называет "единицей первых чисел второго периода". Затем вводятся вторые, третьи числа и т. д. до мириадо-мириадных чисел второго периода. Мириада мириад мириадо-мириадных чисел второго периода (10^2*8*108) образует единицу первых чисел 3-го периода. Единицей первых чисел четвёртого периода будет число 10^3*8*108. Вообще единицей первых чисел n-го периода будет число 10^(n-1)*8*108, единицей m-х чисел n-го периода-число 10^{(n-1)*8*108 + m*8-m}. Так Архимед доходит до мириады мириад мириадо-мириадных чисел мириадо-мириадного периода, т. е. до числа 10⁸*10¹⁶. На этом Архимед останавливается. Но продолжать его путь нетрудно. Вслед за периодами можно ввести какие-нибудь циклы или периоды второго порядка и т. д.

Архимедову систему счисления удобно представить в форме следующей таблицы:

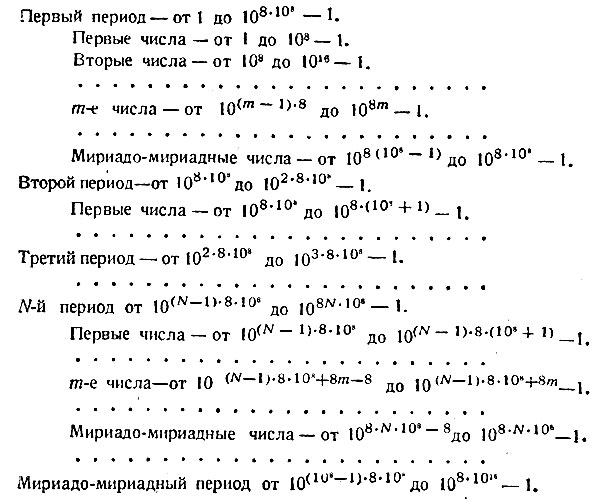
Для того чтобы лучше разобраться в архимедовом счислении и оценить его достоинства, посмотрим, как с его помощью назвать числовые гиганты, о которых говорилось в главе I.

Начнём с "шахматного" числа (стр. 17), равного

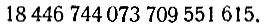
Прежде всего разобьём его на "архимедовы разряды", т. е. на группы по 8 цифр

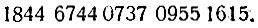
Здесь, очевидно, тысяча восемьсот сорок четыре единицы третьих чисел, шесть тысяч семьсот сорок четыре мириады семьсот тридцать семь единиц вторых чисел, девятьсот пятьдесят пять мириад тысяча шестьсот пятнадцать единиц первых чисел. Это название немногим длиннее нашего (восемнадцать триллионов... и т.д., см. стр. 17).

Для числа Курта Лассвица (10^15*106) мы найдём, что оно равно 10^8(1875001-1), т. е. одной единице сто восемьдесят семь мириад пять тысяч первых чисел первого периода. Мы видим, что для наименования этого числового сверхгиганта не понадобился даже второй период. Даже для числа 9⁹⁹ хватило бы чисел первого периода. Но число 10¹⁰¹⁰ будет уже равняться единице чисел пять тысяч мириад первых (50000001-x) периода тринадцатого.

Вот какое удобное орудие счёта создал Архимед две тысячи двести лет тому назад!