Глава II. Как считали наши предки?

Как люди считали и как называли числа до изобретения письменности, мы точно не знаем. Об этом можно только догадываться. Несомненно одно: человечество овладевало счётом очень медленно. На заре цивилизации люди обходились тремя числами: "один", "два", "много". Прошли, вероятно, многие тысячи лет, прежде чем это "много" отодвинулось дальше. Во всяком случае, ко времени изобретения письменности люди умели уже неплохо считать.

Число и наука о нем

Четыре тысячи лет назад наиболее развитые народы (египтяне, халдеи) умели писать и пользовались не только целыми, но и простейшими дробными числами. Больше того, тогда уже существовали школы, в которых обучали искусству счёта.

В первобытном письме букв не было. Каждая вещь, каждое действие изображалось картинкой. Постепенно картинки упрощались; наряду с изображениями предметов и действий появились особые фигуры, обозначающие различные свойства вещей, а также значки для слов, соответствующих нашим предлогам и союзам. Так возникла письменность, называемая иероглифами; при иероглифической записи каждому значку соответствует не звук, как у нас, а целое слово. Специальных знаков (цифр) для записи чисел тогда не было, но словам "один", "два", "семнадцать" и т. д. соответствовали определённые иероглифы. Их было не так уж много, потому что больших чисел люди тогда не знали. В некоторых странах (например, в Китае и Японии) иероглифическое письмо сохранилось до наших дней.

Вот японские иероглифы, изображающие числа:

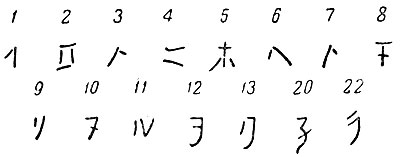
Ещё более замысловаты китайские иероглифы:

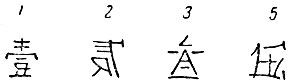
При иероглифической записи говорить о системе счисления не приходится: никакой системы нет. Впрочем, в древнем Египте намечалось нечто, напоминающее отдалённо нашу современную нумерацию.

На следующей ступени культуры появляются буквы, обозначающие звуковые элементы слов. К этому времени люди умеют уже хорошо считать, во всяком случае, они уже знают тысячи и десятки тысяч. Появляются цифры, т. е. особые значки для некоторых чисел, причём любое число (в известных пределах) может быть записано с помощью этих значков. Цифрами обычно служат те же буквы алфавита. Такого рода нумерации были у древних евреев, греков, у римлян и у наших предков--славян. Мы остановимся на римской и на славянской нумерациях.

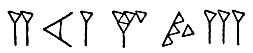
Римские цифры общеизвестны; вот они:

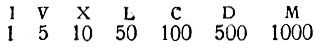
Знаки эти, собственно, не цифры, а заглавные латинские буквы: "и", "вэ", "икс", "эль", "це", "де" и "эм". Но они играли роль цифр: с их помощью римляне могли записать любое число до миллиона. Вот как это делалось. Два и три записывались соответственно так; II, III (т.е. две единицы, три единицы). Четыре записывалось IV: единица, поставленная слева, "отнималась" от пяти. Наоборот, единицы, поставленные справа, прибавлялись: пять, шесть, семь и восемь записывались так:

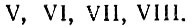
Далее приходилось вводить значок X. Девять записывалось следующим образом: IX (от десяти отнимается единица), а десять, одиннадцать и т. д. так:

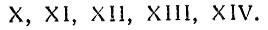
Пятнадцать получалось комбинированием значков десятки и пятёрки: XV; двадцать, тридцать - с помощью десяток:

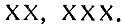
Для сорока и выше приходилось вводить знак L. Сорок один, например, писали так: XLI (десять отнимается, а единица к пятидесяти прибавляется). Для девяноста использовался знак сотни G, именно, 90 записывалось так: ХС). Заметим, что 49 и 99 писали не так: XLIX, XCIX, а так: IL, IС. Сто два писалось СII, триста семьдесят четыре - CCCLXXIV и т. д. Большое число, например, 29 635, записывали следующим образом:

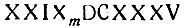
(маленькая буква m^* обозначала тысячи).

^* (Начало латинского слова mille (милле) - тысяча.)

Здесь мы видим уже вполне разработанную нумерацию, очень экономную (с помощью семи цифр записываются числа до миллиона), но неудобную: сравнительно небольшие числа записываются длинно, и никакого облегчения при вычислениях не получается: письменных вычислений производить невозможно, и считать фактически приходится в уме.

Славянская нумерация сходна с латинской тем, что тоже использует для записи чисел буквы алфавита. Она не так экономна, в ней употребляется больше (27) знаков, но сама запись гораздо систематичнее и позволяет значительно упростить выполнение действий. В отличие от римской она пользуется не заглавными, а строчными буквами, снабжёнными к тому же особым знаком- титлом (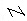) (который, впрочем, употреблялся и в обычном письме для сокращения слов). Вот славянские цифры:

Числа одиннадцать, двенадцать, ... записывались соответственно так: 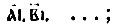двадцать один, двадцать два 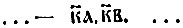и т. д. Титло ставилось только над одной из цифр. Порядок цифр при записи числа был такой же, как в его устном названии. Мы говорим, например, "пятнадцать" (по славянски - пятьнадесять),- называя вперёд цифру единиц, потом десяток. Славяне так и писали: 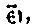т. е. впереди писали пятёрку, а за нею десяток. Наоборот, в числе "двадцать три" мы сперва называем десятки, потом единицы; у славян это отражалось в письме: писали 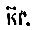Место цифры, её положение в числе не имело значения.

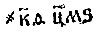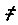С помощью этих знаков легко записывались большие числа. Число 29 946 записывалось, например, таким образом: (знак обозначал тысячи). С помощью повторения знака 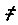можно было записывать очень большие числа. Вот как, например, записывалось число 20 178 073: 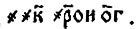. Нетрудно видеть, что эта система записи позволяет выполнять действия "столбиками", почти так же, как это делаем мы теперь.

Скажем несколько слов о названиях чисел в древней Руси, Числа до тысячи назывались почти так же, как сейчас^*. Десять тысяч называлось "тьма", и число это считалось столь огромным, что тем же словом обозначалось всякое неподдающееся учёту множество. В более позднее время (XVI- XVII вв.) появилась своеобразная система наименования чисел, так называемое "великое словенское число"; в этой системе числа до 999 999 называются почти так же, как теперь. Слово "тьма" обозначает не десять тысяч, а миллион. Кроме того, появляются следующие названия: "тьма тем" или "легион" (т. е. миллион миллионов или по теперешнему триллион, т. е. 10¹²); легион легионов ("леодр"), который мы теперь должны записать с помощью единицы с 24 нулями (септиллион - 10²⁴); наконец, леодр леодров ("ворон"), т. е. по нынешнему 10⁴⁸. Про это число наши предки говорили, что "более сего несть разумевати". Впрочем, иногда (рукопись XVII в.) упоминалась ещё "колода", равная десяти "воронам" (10⁴⁹), но при этом оговаривалось, что всего числа несть больше"^**.

^* (Была небольшая разница в произношении: например, один назывался "един", двадцать - "двадесять" и т. д.)

^** (См. брошюру проф. А. В. Васильева - "Целое число" или книгу В. Беллюстина "Как постепенно дошли люди до настоящей арифметики".)

Позиционная нумерация возникла, повидимому, в древнем Вавилоне. Там она приняла такую своеобразную форму, что о ней стоит поговорить подробнее; это будет сделано немного дальше. От вавилонян позиционная нумерация перешла к индусам.

У индусов, как и у многих древних народов, первыми математиками были жрецы. Они ведали календарём и праздниками, следили за небесными светилами и должны были уметь предсказывать различные явления на небе (затмения и т. п.). Для этого нужно было обладать известными математическими познаниями. От существовавшей в старину связи математики с религией сохранился курьёзный пережиток - числовые суеверия; и в наше время есть люди, которые считают, что число 3 приносит счастье, а 13 - несчастье ("чортова дюжина").

Три тысячи лет назад индусы уже пользовались хорошо разработанной нумерацией, хотя в памятниках того времени и не упоминаются числа, большие 100000. В позднейших произведениях индийской письменности встречаются значительно большие числа - до ста квадриллионов (10¹⁷). В одной из сравнительно "молодых" легенд о Будде (ей меньше тысячи лет) говорится, что он знал названия чисел до 10⁵⁴. Впрочем, индусы, повидимому, не представляли себе ясно бесконечности натурального ряда, они полагали, что существует какое-то наибольшее число, известное только богам. Мысль о бесконечности числового ряда -заслуга греческого гения. Об этом будет рассказано в следующей главе.

Совершенно особый интерес, как мы уже упоминали, представляет вавилонская математика. Вавилонская нумерация зародилась почти четыре тысячи лет назад, просуществовала полторы тысячи лет (с XVIII до III в. до н. э.) и пользовалась широким распространением на всём Ближнем Востоке. Она оказала влияние на китайскую, индийскую и греческую математику. Даже в современной науке, как мы увидим, остался её заметный след.

Вавилоняне писали палочками на пластинках из мягкой глины и обжигали потом свои "рукописи". Получались прочные кирпичные "документы", частично уцелевшие до нашего времени; их нередко находят при раскопках в Месопотамии (нынешний Ирак). Поэтому изучить вавилонскую историю вообще и математику в частности удалось довольно хорошо.

На рубеже XIX и XVIII вз. (до нашей эры) произошло слияние двух народов: сумерийцев и аккадян. Каждый из этих народов имел достаточно развитую торговлю, весовые и денежные единицы. Правда, торговля была мелкая, считать приходилось немного, и разработанной нумерации ни один из этих народов не имел. Единицей веса у сумерийцев была "мина" (приблизительно ¹/₂ кг). Денежной единицей служила мина серебра. У аккадян основная единица - "шекель" - была в шестьдесят раз меньше (разумеется, не точно, а приблизительно в шестьдесят раз, но примитивные весы того времени не улавливали разницы). После слияния этих народов "имели хождение" обе системы единиц: минами и шекелями пользовались так, как мы теперь пользуемся килограммами и граммами. А в денежном обращении мины и шекели играли роль наших рублей и копеек, с той только разницей, что более крупная единица равнялась не ста, а шестидесяти мелким единицам. Торговля и хозяйство развивались, обороты росли. Как нам кроме граммов и килограммов нужны тонны, так там появилась более увесистая единица - "талант". Естественно, что раз отношение "шестьдесят" было уже привычным в хозяйственных расчётах, новую единицу установили в шестьдесят раз крупнее имеющейся. Один талант был равен шестидесяти минам.

Как же вавилоняне записывали числа? Они писали палочками, вдавливая их в мягкую глину, поэтому основным графическим элементом был у них клинышек 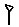или 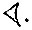Для обозначения единицы использовался один клинышек, поставленный вертикально: 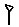; начертание чисел от единицы до девяти естественно и понятно:

Каждое число до девяти включительно изображалось соответствующим количеством клинышков, расположенных столь разумно, что при чтении не приходилось их пересчитывать: количество их сразу бросалось в глаза.

Для десяти был особый знак: 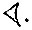Запись чисел второго десятка тоже понятна:

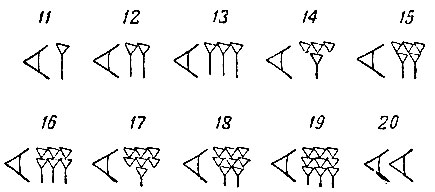
Мы видим, что и эти знаки очень наглядны. Теперь читатель без труда запишет сам любое число в пределах первой сотни. Например, числа 37 и 54 запишутся так:

Числа восьмого и девятого десятков записываются довольно громоздко; но в них ведь не было надобности. Числа, большего пятидесяти девяти, благодаря наличию трёх единиц, вавилонянам записывать вообще не приходилось.

Первоначально мины обозначались более крупными значками, чем шекели. Например, 20 мин 37 шекелей записывалось так:

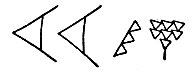
В более поздние времена все знаки записывались совершенно одинаково, и только положение знака показывало, какие единицы он обозначает. Например, 2 таланта 13 мин 41 шекель записывалось так:

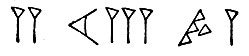
Если приходилось иметь дело только с одной какой-нибудь мерой, то и тогда её никак не обозначали. Сопровождающий текст позволял сразу догадываться, о каких мерах идёт речь.

На рубеже XVIII в. до н. э. появляются чисто математические тексты: таблицы для облегчения вычислений, правила решения задач и т. п. Высокого развития достигает астрономия. В связи с этим приходится, во-первых, всё чаще и чаще сталкиваться с большими числами, а во-вторых, от чисел именованных перейти к отвлечённым. Вместо того, чтобы придумывать другую, используют для новых целей уже разработанную нумерацию. Теперь

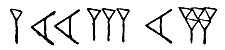
обозначает не обязательно 1 талант 23 мины 15 шекелей - совершенно так же записывается отвлечённое число, содержащее одну единицу третьего, 23 единицы второго и 15 единиц первого разряда, причём единицы каждого последующего разряда в шестьдесят раз крупнее единиц предыдущего. Запись

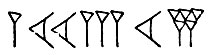
обозначает, по нашему, 1*60² + 23*60 + 15, т. е. 4995. Аналогично записываются четырёх-, пяти-, вообще многозначные числа. Например,

обозначает 2*60³ + 11*60² + 4*60 + 43, т. е. 471 883. Наибольшее число, которое встречается в вавилонских "рукописях", равно 60⁸ + 10*60⁷. Вавилонская нумерация - вполне разработанная нумерация с основанием 60 - шестидесятиричное счисление. Как же обозначали вавилоняне нуль? Как записывали они число 3605, равное 1*60² + 5, т. е. содержащее одну единицу третьего, пять единиц - первого и совсем не содержащее единиц второго разряда? Оказывается, они в течение сотен лет совсем не имели нуля. В нужных случаях они оставляли между цифрами более шрокий промежуток:

Но клинописное письмо очень неудобно для оценки величины промежутков между цифрами, а необходимость переписывать всё от руки приводила к частым опискам. Знак разделения был необходим, и он появился. Начиная с некоторого времени (точную дату установить невозможно), на вавилонских кирпичиках появляется значок 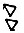, соответствующий нашему нулю.

Теперь 3605 записывают так:

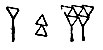
а 65 так:

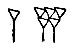
- смешать их больше нельзя.

Однако, введя "позиционную пробку" в середине чисел, вавилоняне так и не додумались ставить её на конце, И до самого падения вавилонской культуры числа "единица", "шестьдесят", "три тысячи шестьсот" записывались одинаково: 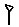. Записывать шестьдесят так: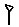 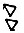вавилонянам не приходило в голову. Только индусы, заимствовавшие у них позиционную нумерацию, научились правильно использовать знак нуля и, введя вместо шестидесяти основание десять, дали счислению его современную форму.

Вавилонская (шестидесятиричная) система счисления удержалась до сих пор при измерении углов и времени. Шестую часть окружности делят на 60 градусов, градус на 60 минут, минуту на 60 секунд. Точно так же час делится на 60 минут, минута на 60 секунд, подобно тому, как талант делился на 60 мин, а мина на 60 шекелей. Скажем, кстати, несколько слов о происхождении названий "минута" и "секунда". Минута (minuta) значит по-латыни: "маленькая"; а секунда (secunda) значит: "вторая". Минуты это были "partes minutae primae" (партэс минутэ прима) - "первые малые части", а секунды - "partes minutae secundae" (партэс минутэ секундэ) - "вторые малые части" градуса или часа.

Подведём итоги. Человечество овладевало счётом медленно. Сотни поколений нужны были для того, чтобы от чисел "один", "два" и "много" перейти к десяткам и сотням. Даже научившись писать, люди долго не имели разработанной нумерации и записывали числа с помощью иероглифов.

У древних евреев, а через них у греков, римлян и славян возникла нумерация с помощью букв алфавита. Эта нумерация просуществовала приблизительно две тысячи лет и была достаточна для целей практической жизни.

Почти четыре тысячи лет назад в Вавилоне возникла позиционная нумерация. В Индии она приняла форму позиционной десятичной нумерации с применением "позиционной пробки" - нуля. У индусов эту систему записи чисел заимствовали арабы, ставшие в VIII - IX вв. н э. одним из самых культурных народов мира. От арабов переняли её европейцы (отсюда -название: арабские цифры).

В наше время позиционная десятичная нумерация совершенно достаточна для нужд науки и практики. При написании очень больших чисел удобно пользоваться знаком показателя степени.

О том, как было выяснено, что натуральный ряд бесконечен, будет рассказано в следующей главе.