Глава I. Наша система счисления

Первобытному человеку считать почти не приходилось. "Один" ,"два" и "много" - вот все его числа. Но нам - современным людям - приходится иметь дело с числами буквально на каждом шагу. Нам нужно уметь правильно назвать и записать любое число, как бы велико оно ни было. Если бы каждое число называлось особым именем и обозначалось в письме особым знаком, то запомнить все эти слова и знаки было бы никому не под силу. Как же мы справляемся с этой задачей? Нас выручает хорошая система обозначений. Совокупность немногих названий и знаков, позволяющая записать любое число и дать ему имя, называется системой счисления, или нумерацией.

Число и наука о нем

Наша нумерация использует для записи чисел десять различных знаков. Девять из них служат для обозначения первых девяти натуральных чисел (1, 2, 3, 4, 5, 6, 7, 8, 9); десятый - не обозначает никакого числа; он представляет собою просто пробку, "пробельный материал" при записи чисел. Значок этот называют нулём и обозначают 0.

Итак, мы имеем девять значков для обозначения первых девяти чисел и десятый значок - нуль - "позиционную пробочку"^*. Значки эти называются цифрами.

^* (О слове "позиционная" см. примечание на стр. 11.)

Как же с помощью десяти цифр записать любое число? Подумаем сначала, как бы мы стали пересчитывать большое число одинаковых предметов, например, спичек. Мы сначала разложили бы наши предметы на кучки по десяти в каждой. Получилось бы некоторое количество десятков (и, может быть, осталось бы несколько предметов, не вошедших в целые десятки). Далее нам пришлось бы пересчитать кучки (десятки). Если бы и кучек (десятков) было очень много, мы сгруппировали бы их в сотни и т. д.

Таким путём мы приходим к основной идее нашей системы счисления - к мысли о единицах различных разрядов. Десять единиц образуют один десяток: иными словами, десять единиц первого разряда образуют одну единицу второго разряда. Десять единиц второго разряда образуют одну единицу третьего. Вообще, десять любых единиц образуют единицу следующего разряда.

Возникает законный вопрос: почему мы стали раскладывать предметы на десятки, а не на пятки или дюжины? Почему единицы второго разряда должны быть в десять, а не в восемь и не в три раза больше единиц первого разряда? Подумав, мы решим, что десятками считать легче. Но почему человеку легче считать именно десятками? Повидимому, объяснением служит тот факт, что наши далёкие предки (как, впрочем, и мы теперь) располагали естественной счётной машиной, связанной с числом десять: именно - десятью пальцами на руках.

Записать какое-нибудь число, например, "пятьдесят семь", пользуясь десятью основными значками и некоторыми связующими словами, можно хотя бы так: "5 единиц второго разряда и 7 простых единиц". Но такой способ записи громоздок. Удобнее и короче было бы записывать числа без помощи слов, одними знаками (цифрами). И в самом деле, мы записываем число "пятьдесят семь" так: 57. Эти две цифры, поставленные рядом, обозначают сумму двух чисел: правое (в нашем примере 7) даёт число простых единиц, а левое (5) - число единиц второго разряда (десятков). Если написаны три цифры подряд, то крайняя правая обозначает простые единицы, следующая (средняя) - единицы второго разряда (десятки), а крайняя левая - единицы третьего разряда, т. е. сотни; значит, 238 обозначает сумму двух сотен, трёх десятков и восьми единиц. Вообще, из двух написанных рядом цифр левая выражает единицы, в десять раз большие, чем правая. Не только сама цифра, но и её место, её позиция^* имеют значение. Поэтому нашу нумерацию называют позиционной нумерацией.

^* (Слово "positio" (позицио) значит по-латыни "положение".)

Напишем по нашей нумерации число "сто два". Здесь одна единица третьего разряда (сотня) и две простых единицы. Записать это так: "12" - нельзя: ведь так записывается число "двенадцать". Писать "12", оставляя место для отсутствующего разряда, неудобно; можно подумать, что здесь широко написанное число "двенадцать" или просто два числа: "один" и "два". Как, далее, отличить в записи следующие числа: "двенадцать" и "сто двадцать"; где оставлять при этом пустое место? Для устранения этих неудобств и введена "позиционная пробка" - цифра нуль. Её пишут на месте отсутствующего разряда. С её помощью числа "двенадцать", "сто два" и "сто двадцать" напишутся по-разному (12; 102; 120).

Всё это очень просто и с детства знакомо. Но как эта простота обманчива! В главе II будет рассказано, как трудно было человечеству додуматься до нуля.

Позиционная десятичная нумерация известна была индусам полторы тысячи лет назад (а может быть, и раньше); в Европу её занесли арабы, вторгшиеся в Испанию в VIII веке нашей эры. Арабская нумерация распространилась по всей Европе и, будучи проще и удобнее остальных систем счисления, о которых речь будет в следующей главе, быстро их вытеснила. До сих пор наши цифры принято называть арабскими. Впрочем, за 1000 лет все цифры, кроме единицы и девятки, сильно изменились. Приводим для сравнения наши (называемые "арабскими") и настоящие арабские цифры:

Скажем несколько слов о принятых у нас наименованиях чисел. Названия первых шести разрядов (единицы, десятки, сотни, тысячи, десятки тысяч, сотни тысяч) очень древни и у разных народов звучат по-разному. Думать о происхождении этих названий - дело филолога, а не математика. Слово "миллион" сравнительно недавнего происхождения. По-итальянски millione (миллионэ) есть увеличительное от mille (милле), что значит "тысяча". По-русски ему могло бы соответствовать несуществующее слово "тысячища". Придумал это слово известный венецианский путешественник XIII в. Марко Поло, которому не хватило обыкновенных чисел, чтобы рассказывать о необычайном изобилии людей и богатств далёкой Небесной Империи^*. Теперь миллионами, десятками и сотнями миллионов называют единицы седьмого, восьмого и девятого разрядов. Тысяча миллионов называется биллионом или миллиардом, а далее для построения числовых наименований, единых во всём мире, используются латинские числительные. Чтобы лучше понять, как строятся названия этих числовых гигантов, вспомним, что каждые три разряда образуют класс: простые единицы, десятки и сотни образуют первый класс; тысячи, их десятки и сотни - второй класс; миллионы - третий класс, биллионы - четвёртый и т. д.

^* (Так в старину называли Китай.)

Чтобы назвать единицу какого-нибудь класса, начиная с четвёртого, надо уменьшить нумер класса на два и к полученному числу, названному по-латыни, прибавить окончание "иллион". Так, единица пятого класса называется "триллион", потому что 5 - 2 = 3, а 3 по-латыни tres (трэс); в сложных же словах tres переходит в tri (звучит так же, как наше "три"). Возьмём единицу двадцать второго класса. Это будет, как нетрудно сообразить, единица 64-го разряда (единице двадцать второго класса предшествует 21 класс, т. е. 21×3 - 63 разряда). Значит, запишется это число так:

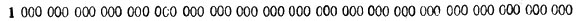
Как же его назвать? От нумера класса отнимаем двойку: 22 - 2 = 20; двадцать по-латыне viginti (вигинти); значит, наше число следует назвать "вигинтиллион".

Построенные таким образом названия мало удобны. Латынь знают не все. Кроме того, названия очень больших чисел громоздки и неудобопроизносимы. Даже хороший латинист вряд ли назовёт число, записанное в виде единицы с пятью миллионами нулей. Впрочем, и записать такое число практически невозможно.

Почему же не реформируют, не изменят способа называть и записывать большие числа? Неужели нельзя внести сюда рационализацию?- Конечно, можно, и даже сравнительно легко. Но в этом нет ни малейшей надобности. Большие числа, подобные написанному выше гиганту, встречаются только в сборниках математических курьёзов, да в некоторых отделах Теории Чисел...

Позвольте, позвольте,- перебьёт читатель: а физика, а астрономия? Ведь за большими числами даже кличка установилась: "астрономические" числа!

Терпенье, читатель! Сейчас будет речь и об "астрономических" числах. Но раньше приведём таблицу наименований единиц высоких разрядов не столько для пользы (польза от неё, как мы скоро увидим, невелика), сколько для удовлетворения любопытства.

Далее следуют: секстиллион, септиллион, октиллион, нониллион, дециллион, ундециллион и т. д.

В некоторых странах, например, во Франции, биллионом называют не тысячу, а миллион миллионов, т. е. единицу 13-го разряда; триллионом называют миллион этих "крупных" биллионов (наш квинтиллион) и так далее, считая классы не по три, а по шесть разрядов. Это несколько упрощает наименование больших чисел.

Поговорим теперь об "астрономических числах"; причём, прежде чем забираться на небо, поищем их на земле. Чему равны, например, поверхность, объём и масса земного шара? Заглянув в учебник географии, находим:

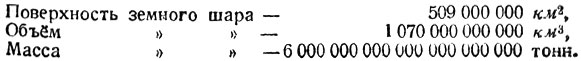
Последнее число (масса) представляет собою 6 единиц 22-го разряда, т. е. шесть секстиллионов.

Все эти числа обладают одной особенностью: это - числа "круглые", оканчивающиеся нулями. Разумеется, ни поверхность, ни объём Земли не могут быть выражены таким "круглым" числом квадратных и кубических километров. "Круглота" здесь кажущаяся. Ведь все геодезические измерения на земной поверхности - приближённые, хотя и производятся очень тщательно; поэтому и числа для поверхности и объёма земного шара суть числа приближённые.

Рассмотрим внимательнее число 509000000 (пятьсот девять миллионов). Шесть нулей справа не обозначают здесь отсутствия тысяч и низших разрядов. Этих разрядов мы либо не знаем, либо сознательно не пишем, так как такая точность нам не нужна. Мы округляем результат, мы говорим: число квадратных километров земной поверхности складывается из пятисот девяти миллионов и какого-то числа тысяч, сотен, десятков и единиц, но какого именно - точно не указываем.

В практической жизни при счёте предметов, которых очень много, например, жителей какой-либо страны или красных кровяных телец в крови человека, а также при измерении различных величин удаётся определить только первые 3 - 4 верные цифры результата. При точнейших измерениях современной физики, которые сопровождаются предосторожностями, превосходящими самые смелые выдумки технической фантазии, удаётся получить семь, в редчайших случаях - восемь верных цифр; если получается целое число больше чем с восемью цифрами, то приходится дописывать на конце нули. Значит, любое большое число, данное практически, можно записать как произведение не более чем восьмизначного (а чаще - трёх-четырёхзначного) числа на "единицу с нулями"^* (например, поверхность земли 509000000 км можно записать так: 509×1000 000 или 509*1 000 000). Числа до миллиарда нетрудно и назвать и записать; следовательно, всё дело в том, чтобы рационально записывать и называть числа, изображаемые единицей с большим числом нулей.

^* (Так коротко называют число, которое имеет первую цифру 1, а все остальные - нули, например, 10, 100, 1000, 10000 000 и т. д.)

Тут нам на помощь приходит понятие степени. Число, изображаемое единицей с нулями, является степенью десяти. Например, сто есть вторая степень десяти (100 = 10²), тысяча - третья степень десяти (1000 = 10³). Вообще, число, изображаемое единицей с нулями, представляет собою такую степень десяти, сколько у него нулей; это можно записать следующим образом:

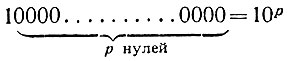
Можно сказать и так: единица n-го разряда представляет собою (n-1)-ю степень десяти (например, миллион - единица 7-го разряда - равняется 10⁶).

Эти соображения позволяют очень коротко и удобно называть и записывать все числа, которые даются нам наукой и жизнью. Рассмотрим, например, массу земного шара. Вот число, которым она выражается:

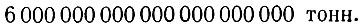
Теперь мы его можем записать так 6*10²¹ тонн, а назвать: "шесть на десять в двадцать первой" (подразумевается: степени). Это и коротко и удобно.

Чтобы привыкнуть к этой системе обозначений и названий, а кстати - познакомиться с величиной чисел, с которыми случается иметь дело современной науке, рассмотрим несколько примеров.

После первой мировой войны 1914-1918 гг. в ряде стран, в том числе и у нас, была хозяйственная разруха, сопровождавшаяся обесцениванием денег. Приходилось выпускать огромные массы бумажек всё более и более высокой номинальной стоимости. Это явление, называемое инфляцией, сопровождалось у нас несколько раз деноминацией, т. е. выпускались деньги сравнительно невысокой номинальной стоимости, причём объявлялось, что один рубль нового выпуска равняется сотне или тысяче рублей предыдущего. Эти деноминации приводили к тому, что на денежных знаках не приходилось печатать очень большие числа: дальше миллионов дело не шло. Но в Германии, где инфляция не сопровождалась деноминацией, существовали боны и даже почтовые марки необычайно высокого номинального достоинства: в десятки и сотни миллиардов марок. На рис. 1 читатель видит несколько почтовых марок с "астрономической" номинальной стоимостью. Высший номинал почтовой марки, выпущенной в Германии,- пятьдесят миллиардов, т. е. 5*10¹⁰ марок; боны бывали ещё более высокого достоинства.

Рис. 1

Классическим примером числового гиганте является награда, которую, если верить старинной легенде, потребовал себе изобретатель шахматной игры. Он, гласит предание, просил за первую клетку доски одно зерно риса, за вторую - два, за третью - четыре и т. д., за каждую последующую - в два раза больше, чем за предыдущую. Эта скромная на вид просьба оказалась невыполнимой: все житницы мира не могут вместить риса, затребованного хитрым изобретателем. Действительно, за первую клетку ему следовало получить одно зерно, т. е. 2-1. За первую и вторую ему следовало 1 + 2 = 3 = 2*2-1 зерно. За первые три клетки 1 + 2 + 4 = 7 = 2*2*2 - 1 зёрен. Мы видим, что за некоторое число а первых клеток придётся отдать

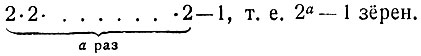
Значит, за все 64 клетки изобретателю причитается 2⁶⁴ - 1 зёрен^*. Число 2⁶⁴ легче всего вычислить, пользуясь сочетательным свойством умножения: ведь 2е4 есть произведение 64 двоек; их можно соединить в группы из 20, из 20, из 20 и из 4 двоек; мы получим:

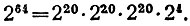
^* (Читатели, знакомые с прогрессиями, сообразят, что числа зёрен, приходящиеся на каждую клетку, образуют геометрическую прогрессию со знаменателем 2, т. е. ^../_.. 1, 2, 4, ..., 2⁶³. Сумма членов такой прогрессии равна )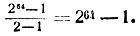

Вычислить 21⁰ = 1024 нетрудно. Помножив 1024 на себя, получим 2²⁰= 1048 576. Следовательно,

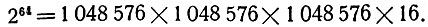
Остаётся сделать скучное, но не трудное умножение. Окончательно получим:

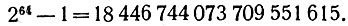
Число это читается так: восемнадцать квинтиллионов четыреста сорок шесть квадриллионов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать. Оно приблизительно равно 18*10¹⁸ (читается так: "восемнадцать на десять в восемнадцатой").

Следующий курьёзный пример числового гиганта мы заимствуем у немецкого математика и популяризатора Курта Лассвица. Он поставил такой вопрос: сколько томов должна насчитывать библиотека, которая содержала бы не только всё, что когда-либо было написано людьми, но и всё, что когда-либо будет написано или хотя бы подумано; которая содержала бы все настоящие, прошедшие и будущие научные теории, все фантазии, включая самый дикий бред сумасшедшего, словом- решительно всё?

Несмотря на явную нелепость постановки вопроса, задача эта имеет решение. Правда, нельзя найти наименьшего числа томов, нужного для такой "универсальной" библиотеки. Но возможно подсчитать такое (сильно завышенное) число томов, при котором эта "универсальность" наверняка осуществится.

Вообразим наборную кассу из 1000 гнёзд. Этого с излишком достаточно для всех букв алфавита (строчных, прописных и иностранных), знаков препинания, математических знаков, "пустышек" разной величины и т. д. Допустим, что в каждом гнезде имеются многие миллионы соответствующих букв, знаков и т. д.- литер, как говорят наборщики. С помощью этих литер будем набирать книги по 5000000 знаков в каждой. Это будут книги большого формата, напечатанные мелким убористым шрифтом, каждая по 1000 страниц.

Приступим теперь к решению задачи. Рассмотрим всевозможные книги указанной величины, которые можно набрать с помощью нашей кассы. На первом месте, т. е. в левом верхнем углу первой страницы, может стоять любой знак, т. е. любая буква или пустышка. Всего возможно 1000 комбинаций. Вслед за каждым из знаков, стоящих на первом месте, можно поставить снова любой из тысячи знаков, т. е. первое и второе места в книге могут быть заняты 1000×1000 = 1000², различными способами. Первые три места могут быть заняты 1000²×1000= 1000³ различными способами (ведь к каждому из 1000² возможных расположений первых двух может быть присоединён любой из тысячи знаков). Точно так же для четырёх первых знаков возможно 1000⁴ расположений, для строчки из 70 знаков - 1000⁷⁰. Наконец, для всей книги возможно 1000^5000000 расположений знаков, или, иными словами, 1000^5000000 книг исчерпают всё, что только можно мыслить напечатанным. Почти всё будет невероятной чепухой (ведь будут и "книги", составленные из одних "пустышек", или из одних запятых, или из одних букв "а"). Но будут попадаться и такие экземпляры, в которых случайно окажется нечто разумное, и таких экземпляров, несмотря на их редкость (это будут единицы на ультрамиллиарды чепухи), всё же будет чудовищно много. Сюда обязательно войдёт всё разумное, что когда-либо знал, знает или будет знать человек.

Вернёмся к ответу на нашу задачу, к числу 1000^5000000. Число это представляет собою произведение пяти миллионов чисел, каждое из которых равно тысяче. Но тысяча есть произведение 10×10×10. Заменив в нашем числе каждую тысячу этим произведением, мы получим произведение пятнадцати миллионов десятков, т. е. 10^15000000 (назовём мы это число: "десять в пятнадцатимиллионной"). Назвать его с помощью обычной нумерации практически невозможно, а для записи его понадобился бы громадный том более чем в 1000 страниц. Здесь особенно наглядно выступает преимущество сокращённой записи.

Наше число (вернее - число Курта Лассвица) можно записать ещё короче, если заметить, что сам показатель 15 000 000 может быть представлен так: 15*10⁶. Значит, число Курта Лассвица можно записать в следующей "трёхэтажной" форме: 10^15*106.

С такой "трёхэтажной" записью мы встречаемся в известной задаче-шутке о самом большом числе, которое можно записать с помощью трёх девяток. Ответом служит не наивное 999 и не внушительное 9⁹⁹ или 99⁹, а "трёхэтажный" гигант 9⁹⁹. Он много больше числа Курта Лассвица. Запись его с помощью нашей системы счисления раз в 20 с лишним "длиннее". Число это (9⁹⁹) приблизительно равно 4*10^369693099 (четыре на десять в триста шестьдесят девять миллионов шестьсот девяносто три тысячи девяносто девятой; его и по сокращённому способу назвать трудно!):

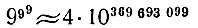
(≈ - знак приближённого равенства).

Рядом с этими исполинами "астрономические" числа кажутся жалкими карликами. Рассмотрим, например, радиус вселенной; вернее - радиус доступной нам вселенной, так как всю вселенную мы представляем себе бесконечной. Самые отдалённые светила, доступные современным сверхмощным телескопам, это - грандиозные туманности, состоящие из миллиардов солнц, подобных нашему: они так далеки, что и в телескопы кажутся еле заметными звёздочками. Свет от них до нас доходит в 150 000 000 лет; это значит, что они отстоят от нас почти на 2*10²¹ километров. Всё, что дальше этого, нам, при современном состоянии науки, недоступно.

Итак, радиус видимой вселенной равен 2*10²¹ км, или 2*10²¹*10⁵ = 2*10²⁶ см (в 1 км содержится 100000 = 10⁵ см). В физике все длины принято выражать в сантиметрах, поэтому и мы выразили радиус вселенной в сантиметрах. Это число нетрудно назвать: ведь 2*10²⁶ равно двум единицам двадцать седьмого разряда или двумстам единицам девятого класса. Отнимая от девяти два, получим семь (см. стр. 12 - как называть большие числа). Значит, название нашей единицы должно происходить от латинского septem (семь), т. е. радиус вселенной равен двумстам септиллионам сантиметров.

Зная радиус, нетрудно определить и объём вселенной: он равен, примерно, 2*10⁸¹ см³. Это - невероятно большое число, совершенно не поддающееся наглядному восприятию. И всё же оно ничтожно мало по сравнению с гигантами, рассмотренными нами выше.

Подведём итог этой главе. Для обозначения и записи чисел мы пользуемся позиционной десятичной нумерацией. Позиционной она называется потому, что значение цифры зависит от её положения - места в ряду других цифр написанного числа; десятичной - потому, что из двух написанных рядом цифр левая обозначает единицы, в десять раз большие, чем правая. Для обозначения и записи чисел в пределах миллиарда эта система очень удобна и вряд ли желательно какое-либо её изменение. Для записи очень больших чисел она неудобна (получаются очень "длинные" числа), а для их названий - практически совсем неприменима. Чтобы устранить эти неудобства, пользуются понятием степени числа. Представляя число в виде произведения относительно небольшого числа на степень десяти, мы без труда записываем и называем все числа, встречающиеся в науке и в жизни.