3. Рождение буквенной алгебры

I. II-I вв. до н. э. были временем стремительного возвышения Рима, который покорял и обращал в провинции одно за другим эллинистические государства, города и союзы городов материковой Греции. В 30-гг. до н. э. пало последнее из эллинистических государств - Египет, и была основана Римская империя.

В результате этого положение бывших эллинистических государств коренным образом меняется. С одной стороны, прекращаются разорительные войны и прямой разбой, что приводит к более устойчивому экономическому положению, но, с другой - эллинистические государства теряют самостоятельность и, по образному выражению Плутарха, всегда сознают, что над их головой занесен "римский сапог". И все же греческая наука вновь оживает. В первые века н. э. Александрия остается научным и культурным центром древнего мира. Рим никогда не мог сравниться с ней в этом отношении. По существу, он так и не приобщился к глубинам эллинской мысли. Римляне с презрением относились к математике и другим абстрактным наукам, ценя только узко практические знания. Но и этим должны были заниматься греки, сирийцы и другие покоренные народы, а не римляне, уделом которых была власть над миром. Как писал Вергилий:

Тоньше другие ковать будут жизнью дышащую бронзу,-
Верю тому,- создадут из мрамора лики живые, 
Красноречивее будут в судах, движение неба 
Тростью начертят своей и вычислят звезд восхожденья, 
Ты же, римлянин, знай, как надо народами править.

Конец I и II в. н. э. обычно называют греческим возрождением, имея в виду, что это было временем жизни и творчества таких великих писателей, как Плутарх и Лукиан. Но такой же расцвет мы наблюдаем и в естественных науках: в I в. в Александрии работал прекрасный математик и талантливый инженер-изобретатель Герон, который первым открыл движущую силу пара, в конце века - математик и астроном Менелай, создатель системы геометрии и тригонометрии на сфере (первой системы неевклидовой геометрии), а во II в.- знаменитый астроном и математик Клавдий Птолемей, создавший геоцентрическую модель Солнечной системы (она просуществовала вплоть до XV- XVI вв.). Уже в творчестве этих ученых наметился поворот к вычислительной математике, к расширению понятия числа, к отказу от геометрической алгебры.

Эти тенденции проявились с особой силой в творчестве величайшего алгебраиста древности Диофанта Александрийского, о жизни которого мы почти ничего не знаем. Правда, в Палатинской антологии, составленной ученым грамматиком и арифметиком Метродором Византийским (IV в. н. э.), сохранилась эпитафия, которая гласит:

Прах Диофанта гробница покоит: дивись ей - и камень 
Мудрым искусством его скажет усопшего век. 
Волей богов шестую часть жизни он прожил ребенком, 
И половину шестой встретил с пушком на щеках. 
Только минула седьмая, с подругою он обручился. 
С нею пять лет проведя, сына дождался мудрец, 
Только полжизни отцовской возлюбленный сын его прожил
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое гора. 
Тут и увидел предел жизни печальной своей*.

^* (Приведенный перевод с древнегреческого принадлежит С. П. Боброву.)

Отсюда нетрудно подсчитать, что Диофант прожил 84 года. Однако для этого вовсе не нужно владеть "мудрым искусством его". Достаточно уметь решать уравнение 1-й степени с одним неизвестным, а это умели делать египетские писцы еще за 18 веков до н. э.

На этом наши сведения о Диофанте кончаются. Однако его творчество сыграло настолько большую роль в истории алгебры, что ученые потратили немало усилий, чтобы определить время его жизни. Проследим за ходом их рассуждений. Прежде всего известно, что Теон Александрийский в своих комментариях к "Альмагесту" Клавдия Птолемея привел отрывок из сочинений Диофанта. Поскольку деятельность Теона падает на вторую половину IV в. н. э., очевидно, Диофант не мог жить позднее середины IV в. Этим определяется верхний предел промежутка возможного времени жизни Диофанта. С другой стороны, сам Диофант в своей работе "О многоугольных числах".дважды упоминает Гипсикла, математика, жившего в Александрии в середине II в. до н. э. Итак, нижним пределом является вторая половина II в. до н. э. Таким образом, получаем промежуток в 500 лет!

Сузить этот промежуток попытался П. Таннери, известный историк науки, издатель критически проанализированного текста сочинений Диофанта, который теперь принят в качестве канонического. В библиотеке Эскуриала он нашел отрывок из письма Михаила Пселла, византийского ученого XI в., текст которого был искажен при переписках. После восстановления Таннери один из отрывков письма может быть переведен так: "Что касается этого египетского метода, то Диофант рассмотрел его более точно и ученнейший Анатолий, после того как собрал наиболее важные части этой науки, посвятил их своему другу Диофанту". Известно, что Анатолий Александрийский составил "Введение в арифметику" в десяти частях, фрагменты из которой дошли до нас в передаче Ямблиха (IV в. н. э.). Известный историк церкви Евсевий (IV в. н. э.) также упоминает Анатолия и превозносит его. за глубокие познания в арифметике, геометрии и астрономии. Но Анатолий жил в Александрии в середине III в. н. э., а в 270 г. покинул ее, чтобы принять сан епископа Лаодикийского. Таким образом, если Таннери правильно прочел письмо Пселла, то Диофант жил в середине III в. н. э.

Это подтверждается еще и тем что сама "Арифметика" Диофанта посвящена "достопочтенному Дионисию", который, как это видно из введения к I книге, интересовался наукой о числах и ее преподаванием. Между тем с 231 по 247 г. во главе Александрийского христианского училища для юношества был Дионисий, ставший в 247 г. епископом Александрийским. По предположению Таннери именно ему и была посвящена "Арифметика".

Поэтому обычно теперь считают, что Диофант жил около 250 г. Однако существуют свидетельства, правда, весьма поздние, которые ставят эту дату под сомнение. Дело в том, что первым европейским математиком, серьезно изучавшим "Арифметику" Диофанта, был Рафаэль Бомбелли. В предисловии к своей "Алгебре" (1572 г.) Бомбелли писал, что он нашел в библиотеке Ватикана замечательную рукопись, посвященную науке о числах, составленную "неким Диофантом, греческим автором, жившим в эпоху Антонина Пия". Эту же дату повторяют затем Виет, Ферма и другие ученые XVI-XVII вв.

Но Антонин Пий был римским императором в середине II в. н. э., т. е. время жизни Диофанта отодвигается на 100 лет назад, и он оказывается современником астронома Клавдия Птолемея и деятелем "греческого возрождения".

Откуда же почерпнул свои сведения Бомбелли? Это абсолютно неизвестно. Можно только предположить, что он читал в библиотеке Ватикана какие-то дополнения к рукописи Диофанта, которые были с тех пор утеряны. Быть может, новые находки на арабском Востоке или в недрах европейских библиотек прояснят этот вопрос. Пока что наиболее вероятным временем жизни Диофанта представляется столетие с середины II в. по середину III в. н. э.

Основным произведением Диофанта была "Арифметика", которая, как он сам об этом пишет, была разделена на 13 книг. Из них до нас дошли 6 книг на древнегреческом языке, а недавно были найдены и опубликованы еще 4 книги в арабском переводе, которые также приписываются Диофанту.

"Арифметика" явилась поворотным пунктом в развитии алгебры и теории чисел. Именно в ней произошел окончательный отказ от геометрической алгебры. Но это вовсе не означало, что алгебра вернулась к тому состоянию, которое было у нее в Вавилоне. Нет, в "Арифметике" алгебра обрела новый язык, гораздо более оперативный и удобный, чем язык геометрии. Именно здесь родилась буквенная алгебра.

Введение к "Арифметике" представляет собой краткий трактат по алгебре. Оно начинается с описания символики. Диофант называет неизвестное "числом" ('αριυμóς) и применяет для него знак ς, который уже встречался у Герона и в мичиганском папирусе (II в. н. э.). Возможно, что этот знак представляет последнюю букву в слове 'αριυμóς, т. е. это "концевая сигма". Дело в том, что греки пользовались алфавитной нумерацией, т. е. все буквы их алфавита имели числовые значения; первые девять букв α, β, ... , υ означали числа 1, 2, ..., 9; следующие девять букв ι, א, ... - последовательные десятки: 10, 20, ..., 90, наконец, последние 9 букв - сотни от 100 до 900^*. Над буквами, означающими числа, сверху ставили черточку, чтобы не спутать их со словами. Например, число 121 в греческой записи выглядело так: (ρאα)_-. При этом буква σ - "сигма" - имела числовое значение 200, но в конце слова она записывалась иначе, а именно: ς. Этот-то знак, не имеющий числового значения, и мог быть взят для обозначения неизвестного. После этого Диофант вводит 6 положительных и 6 отрицательных степеней неизвестного. Символы для положительных степеней являются сокращениями их греческих названий. Квадрат неизвестного (динамис - сила, степень) Диофант обозначает символом Δ^Y, куб (кубос - куб) - K^Y, четвертую степень (динамодинамис - квадрато-квадрат)- Δ^YΔ, пятую степень (динамокубос - квадрато-куб) - ΔK^Y, шестую степень (кубокубос - кубо-куб) - K^YK.

^* (Поскольку в греческом алфавите всего 24 буквы, то к нему для нужд нумерации добавляли еще 3 "архаические буквы" - "вау", "коппа" и "сампи".)

Отрицательные степени Диофант определяет как дроби с числителем единица и знаменателем, равным соответствующей степени неизвестного. Для отрицательных степеней вводится знак, напоминающий косой крест, который добавляется справа к символу соответствующей положительной степени.

У Диофанта есть также специальный символ для неизвестного в нулевой степени, M, который он (так же как современный алгебраист) не отождествляет с числом 1. Например, многочлен (1*x² + 10x + 1*x⁰), который мы записываем обычно более кратко x² + 10x + 1, отождествляя 1*x² с x² и 1*x⁰ с 1, в символике Диофанта выглядит следующим образом:

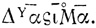
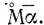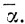Отождествления с Диофанта нет и не может быть. Это происходит из-за того, что Диофант не ввел специальных знаков для сложения и умножения. Их отсутствие восполняется строго определенным порядком записи степеней неизвестного и коэффициентов, при котором коэффициент всегда следует за знаком степени. При этом для того чтобы свободный член не сливался с коэффициентом при старшей степени, необходим символ для нулевой степени неизвестного, выступающий в роли знакоразделителя.

Помимо перечисленных символов, Диофант употребляет еще знак ▫ для неопределенного квадрата.

Заметим, что введение шести первых степеней неизвестного означало решающий шаг на пути построения алгебры, независимой от геометрии. Ведь только три первые степени неизвестного ζ, Δ^Y и K^Y могли быть истолкованы геометрически как образы в трехмерном пространстве. Введя четвертую, пятую и шестую степени, а также обратные к ним величины, Диофант решительно порвал с классической геометрической алгеброй. Этот шаг, по-видимому, оставался непонятым многими из его современников и многими из последующих ученых. Так, Папп Александрийский писал (конец III в. н. э.): "Нельзя говорить о данном отношении какого-нибудь предмета, построенного на четырех прямых, к предмету, построенному на остальных, потому что не существует ничего, что заключало бы больше, чем три измерения. Однако незадолго до нас стали позволять себе выражаться подобным образом, не указывая, впрочем, при этом на что-либо сколько-нибудь вразумительное".

После введения символов для степеней неизвестного Диофант формулирует правила умножения x^m на xⁿ, где |m|≤6, |n|≤6; |m + n|≤6, которые в наших обозначениях^* можно записать как x^mxⁿ = x^m+n.

^* (Мы будем в дальнейшем пользоваться для обозначения степеней неизвестного современными знаками.)

При этом он выделяет два правила, носящих совершенно общий характер.

1. "Всякий вид (ειδοζ), умноженный на одноименную с ним часть, производит единицу", т. е. произведение степени x^m на обратную ей величину x^-m дает 1.
2. "Так как единица остается всегда неизменной, то умноженный на нее вид остается тем же видом", т. е. существует такой элемент 1, что для каждого m
   x^m*1 = x^m.

Нетрудно видеть, что здесь впервые в явном виде выделены основные теоретико-групповые свойства операции умножения.

Приходится только удивляться глубине проникновения Диофанта в алгебраическую суть вопроса.

Наконец, Диофант вводит знак 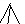(который он сам характеризует как "перевернутую и укороченную букву ψ), отвечающий нашему знаку "минус". О нем мы будем говорить подробнее в следующем пункте. Сейчас скажем только, что при записи многочленов или уравнений Диофант выписывает сначала подряд все положительные члены, а затем после знака А - все отрицательные. Например, многочлен

в записи Диофанта выглядел бы так:

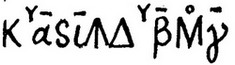
(здесь ).

При записи уравнений Диофант применяет знак равенства 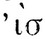, представляющий собой две первые буквы слова 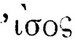- равный. Например, уравнение x³ = 2 - x в его записи будет

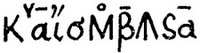
В конце введения формулируются правила преобразования уравнений, попавшие в Европу через арабов и получившие поэтому арабизированные названия "ал-джебр" и "ал-мукабала". Эти правила разрешают прибавление к обеим частям уравнения одинаковых членов и приведение подобных членов.

Таким образом мы видим, что во введении к "Арифметике" Диофант изложил в аксиоматической форме основные алгебраические понятия и элементы алгебраической символики, т. е. теоретические основы той части математики, которая в дальнейшем получила название алгебры, а не арифметики.

Однако анализ решений задач позволяет обнаружить в самой "Арифметике" более широкие теоретические основания, чем те, которые явно изложены во введении. Прежде всего это относится к числовой области Диофанта.

II. Числовая область Диофанта. Во введении дается традиционное определение числа как некоторого количества или множества единиц. В дальнейшем при решении задач под числом уже понимается любое положительное рациональное число. Решение задачи Диофант всегда ищет в области положительных рациональных чисел. В то же время когда возникает угроза получения отрицательного или иррационального решения, Диофант, чтобы прийти именно к положительному и рациональному решению, проводит дополнительный анализ условий задачи. Часто этот анализ сложнее и тоньше самого способа решения. Таким образом, казалось бы, напрашивается вывод, к которому обычно приходили исследователи "Арифметики", что Диофант работает в области положительных рациональных чисел. С этим нельзя согласиться в полной мере. Верно лишь то, что Диофант ищет решения задач в области положительных рациональных чисел.

Как хорошо известно, одних положительных рациональных чисел недостаточно для построения алгебры. Действительно, для этого нужна область, в которой можно беспрепятственно производить все четыре действия арифметики, т. е. поле.

Как же мог построить свою алгебру Диофант?

Мы постараемся показать, что он ввел отрицательные числа, свободно оперировал с ними, хотя они еще и не получили у него права гражданства.

Действительно, в определении (IX) введения он сформулировал правило знаков:

"(IX) Недостаток 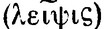умноженный на недостаток, дает наличие (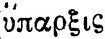); недостаток же, умноженный на наличие, дает недостаток; знак же для недостатка - 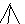, укороченное и опрокинутое вниз ψ".

Здесь словом "недостаток" переведено греческое слово 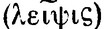. Это слово - специальный математический термин, в обычных словарях оно отсутствует. Произведено оно от глагола λει'πω, одним из значений которого является "недоставать", "не хватать". Поэтому в русском переводе был выбран термин "недостаток". Поль Таннери в своем классическом издании "Арифметики" Диофанта переводит термин 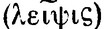на латынь словом "minus" - меньше, а термин 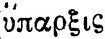, означающий по-гречески "существование", "бытие", а во множественном числе - "имущество" - словом "plus" - больше. Во введении к "Арифметике" 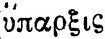является специальным термином для обозначения положительного числа. Заметим еще, что λεε'ψι'ζ нельзя переводить словом "вычитаемое", как это иногда делают, так как вычитание Диофант обозначает словами, производными от глагола α'φαιρεω - отнимать. К тому же правило (IX) он приводит до рассмотрения многочленов.

Таким образом, Диофант вводит отрицательные числа, по существу, аксиоматически, формулируя для них "правило знаков":

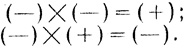
Диофант не определяет специальных правил для сложения и вычитания отрицательных чисел, но пользуется ими при оперировании с многочленами, имеющими как положительные, так и отрицательные коэффициенты. Так, например, в ходе решения задачи III. 8 "Арифметики" Диофанту требуется из x² + 4x + 1 вычесть 2x + 7. В результате он получает x² + 2x - 6. Здесь Диофанту для вычитания многочленов необходимо произвести вычитание их свободных членов 1-7 = -6, т. е. из меньшего числа вычесть большее, что невозможно без введения отрицательных чисел. Другой интересный пример мы находим в задаче VI. 14, по ходу решения которой из 54 вычитается 90 - 15x² и получается 15x² - 36. Здесь, кроме того, что из меньшего числа вычитается большее (54-90 = -36), производится также вычитание одночлена (-15x²). При этом Диофант, очевидно, пользуется правилом -(-a) = a. Это показывает, что он владел правилами знаков не только для умножения, но и для вычитания. Последние, видимо, были достаточно хорошо известны, так как Диофант не счел нужным их специально формулировать.

Наконец, отрицательные числа неявно встречаются и в промежуточных вычислениях. Например, в задаче II.11 Диофант полагает сторону некоторого квадрата равной x-2, при этом в решении участвует только квадрат (x-2)², а не его сторона. В конце задачи Диофант, решая уравнение относительно x, находит x = 15/8. Легко видеть, что тогда выражение x - 2 = -¹/₈<0. Это, однако, не смущает Диофанта, так как для нахождения решения задачи он оперирует со значением квадрата (-¹/₈)², т. е. с положительным числом, ¹/₆₄. Аналогичная ситуация имеет место в задачах II. 11-13, 20, 21, 23, 28, 29, 32 и многих других. Таким образом, хотя решения задач по традиции ищутся в области положительных рациональных чисел, в ходе решения задач Диофант вводит отрицательные числа и оперирует с ними, расширяя тем самым числовую область до поля рациональных чисел.

III. Выяснив, что представляет собой числовая область Диофанта, мы теперь рассмотрим возможности его алгебраической символики.

С помощью описанных им во введении алгебраических символов Диофант может записать, во-первых, любой многочлен от неизвестного x, степень которого ≤6, и, во-вторых любой многочлен от n-1, степень которого также ≤6. При решении некоторых задач Диофант работает и с рациональными функциями от x, степень числителей и знаменателей которых ≤6.

Мы видим, что символика Диофанта характеризуется, во-первых, ограничением на число неизвестных и, во-вторых, на величину степени. Возникает вопрос: насколько каждое из этих ограничений существенно?

Начнем с ограничения на степень. Диофант вводит символику только для первых шести степеней неизвестного. Разумеется, ограничение именно шестой степенью не принципиально. Число 6 выбрано в качестве верхней границы для вводимых степеней, видимо, потому, что многочленами большей степени Диофанту просто не приходится пользоваться.

Уже в арабских книгах "Арифметики" встречаются 8-я и 9-я степени неизвестного, которые, возможно, были добавлены кем-нибудь из комментаторов.

Теперь мы перейдем к другому важному ограничению - на число неизвестных.

Алгебра Диофанта на первый взгляд есть алгебра рациональных функций от одного неизвестного. Но большинство его задач сводятся к неопределенным уравнениям от многих неизвестных (часто пяти, шести и больше). Например, задача II.8 формулируется так: "Разложить заданный квадрат на два квадрата". Для ее записи в виде уравнения необходимо два неизвестных: x² + y² = a².

Задача III. 19 эквивалентна системе:

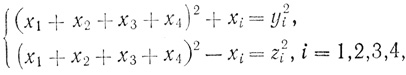
т. е. в записи должно участвовать 12 неизвестных. Как же Диофант записывает эти уравнения и оперирует сними?

Уже в математике Древнего Вавилона решение алгебраической задачи с конкретными числовыми данными служило одновременно двум различным целям: получению численного решения задачи и демонстрации общего приема решения целого класса однотипных задач. Как мы видели, имелся класс задач на отыскание "длины" и "ширины", если заданы сумма (или разность) их и "площадь", т. е. произведение "длины" на "ширину". При этом составлялись группы таких задач, имеющих одни и те же, заранее подобранные ответы. Это делалось для того, чтобы выпуклее показать общность алгоритма их решения. Действительно, в этом случае центр тяжести переносился на сам алгоритм, так как численные ответы были заранее известны и могли служить только для проверки правильности применяемого способа решения.

В "Арифметике" Диофанта роль числовых параметров существенно расширяется. Обычно для решения задачи Диофант представляет все искомые числа как рациональные функции от одного неизвестного и параметров. Параметрам, правда, придаются конкретные числовые значения, но при этом, как правило, Диофант оговаривает, что они могли бы быть и любыми другими числами. Эти-то параметры и играют в "Арифметике" роль дополнительных переменных.

Так, при решении задачи II.8 (формулировку см. ранее) Диофант принимает a² = 16, один из искомых квадратов берет в качестве неизвестного t² (мы применяем для простоты более привычные нам обозначения), а сторону второго составляет "из некоторого количества t минус столько единиц, сколько их найдется в стороне 16-ти, пусть это будет 2t - 4, т. е. Диофант хочет положить второй квадрат равным (kt - a)², но поскольку у него нет знаков ни для произвольного параметра k, ни для заданного произвольного числа а, он, объяснив, что k - произвольно, а a - сторона заданного квадрата, берет 2t - 4, где 2 есть и число "2", и символ для произвольного рационального числа.

Сделаем подстановку Диофанта:

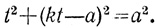
Откуда

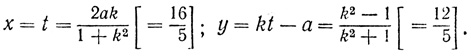
Однако иногда оказывается, что произвольно выбранные значения для параметров не годятся, т. е. основное неизвестное получается отрицательным и иррациональным. Тогда оказывается необходимым предварительное исследование задачи для выяснения того, какие ограничения следует наложить на выбор параметров. Так, например, задача IV.8 сводится к системе:

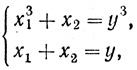
при решении которой Диофант полагает: x₂ = t, x₁ = βt, где β = 2.

Из второго уравнения он находит:

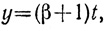
а из первого

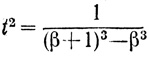
Поскольку β = 2, то t² = 1/19, т. е. t - иррационально. Диофант анализирует, как t² составлено из параметра β, иначе говоря, находит t² = f^-1 (β), где f(β) = (β+1)³ - β³, откуда делает вывод, что исходная система будет иметь рациональное решение, если

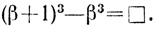
Он берет β в качестве нового неизвестного β = z (обозначает его той же буквой, что и первоначальное) и получает вспомогательное уравнение:

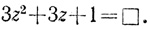
Решая это последнее уравнение своим методом, т. е. полагая ▫ = (kz - 1)², Диофант получает:

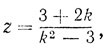
другими словами, это означает, что параметр β можно выбирать только из класса чисел

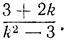
Отметим, что знаком ζ (см. стр. 37) в процессе решения одной и той же задачи Диофант может обозначать последовательно различные неизвестные. Так, в рассмотренной задаче ζ - это сначала прибавляемое число x², а затем неизвестное во вспомогательном уравнении.

Замечательно, что Диофант часто сознательно выбирает для несвободных параметров числа, которые не приводят к решению, чтобы показать, как надо проводить анализ задачи.

То обстоятельство, что Диофант смотрит на параметры не как на конкретные числа, а, скорее, как на символы, ярко подтверждается при решении задач III.10 и III. 11. Рассмотрим первую из них:

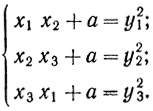
Диофант принимает a = 12 и полагает y₁ = ε, (ε = 5), тогда x₁x₂ = ε² - a, и он принимает x₁ = (ε² - a)t, x₂ = 1/t. Этим первое уравнение обращается в тождество. Затем он полагает y₂ = δ, (δ = 4), тогда x₂x₃ = δ² - a, но x₂ = 1/t, значит x₃ = (δ² - a)t. Остается удовлетворить третьему уравнению:

При выбранных Диофантом параметрах получаем:

Это уравнение имеет рациональное решение t = 1, y₃ = 8, а значит, оно имеет и бесконечно много других рациональных решений, которые могут быть найдены методом, изложенным во II книге "Арифметики". Но Диофант как будто не замечает этого. Ведь существование решения уравнения при δ = 4 и ε = 5 получилось чисто случайно! И Диофант ищет общие условия, которые надо наложить на параметры ε и δ, чтобы было обеспечено существование рационального решения.

Таким образом, в алгебраическом формализме Диофанта наряду со знаками для неизвестного и его степеней большую роль играют знаки конкретных чисел, которые несут дополнительную нагрузку, выполняя функцию параметров. При этом они могут служить:

1. знаками свободных параметров,
2. знаками для несвободных параметров (параметров, удовлетворяющих некоторым дополнительным условиям).

Алгебраический формализм Диофанта представляет, как мы думаем, особый этап в развитии алгебры, характеризующийся тем, что отсутствие нескольких неизвестных и буквенных обозначений для параметров компенсируется полифункциональным использованием знаков для единственного неизвестного и его степеней и знаков для конкретных чисел. Этот этап, начало которому было положено "Арифметикой" Диофанта, продолжался вплоть до второй половины XVI в. Только в это время в алгебре были введены сначала знаки для второго, третьего и т. д. неизвестных (Бомбелли и Стевин), а затем знаки для параметров и буквенное исчисление (Ф. Виет).

Развитие алгебры показало, что алгебраический формализм Диофанта, хотя и менее мощный, чем современный, способствовал замечательным успехам как в изучении диофантовых уравнений, так и позднее, в решении определенных уравнений 3-й и 4-й степеней.

Здесь уместно обратить внимание читателя на тот факт, что основной проблемой, при исследовании которой развивались и совершенствовались методы алгебры, была не проблема решения уравнений в радикалах, которая занимала сравнительно мало места, а проблема решения неопределенных уравнений. Мы видели, что именно с ней было связано первое введение буквенной символики, возникновение алгебраического формализма, о котором мы писали, а также расширение понятия числа до поля всех рациональных чисел. Мы покажем, что и дальнейшее развитие алгебры вплоть до введения буквенного исчисления было связано с исследованием неопределенных уравнений.