4. Создание буквенного исчисления

I. Диофант был последним великим математиком древности. После него работали только более или менее талантливые комментаторы. Но вскоре и такие работы прекратились. Античная наука и культура погасли вместе с гибелью всего античного общества. Факел знания был передан на Восток. В течение более восьми веков (VII-XV вв.) научные исследования велись народами, населявшими Иран, Среднюю Азию, Малую Азию, Северную Африку. В VII-VIII вв. они были объединены в Арабский халифат, и хотя огромное государство арабов оказалось недолговечным и вскоре распалось на части, господствующим научным языком стал арабский.

В VIII в. в Багдадском Доме мудрости работала целая коллегия переводчиков и комментаторов. Были переведены "Начала" Евклида, многие сочинения Архимеда, философские трактаты Аристотеля.

Математики стран Востока познакомились с "Арифметикой" Диофанта, которая была переведена на арабский язык в начале X в., и усвоили содержащиеся там алгебраические методы. Ал-Караджи (X в.) в своей книге "Ал-Фахри" ввел бесконечный ряд степеней неизвестного, заметив, что степени образуют цепь пропорций, которую мы можем записать так: 1:x = x:x² = x²:x³ = ... .

К этому ряду добавляется, как и у Диофанта, ряд "частей", т. е. отрицательных степеней неизвестного:

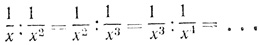
Алгебра в это время уже воспринимается как самостоятельная наука - наука о решении уравнений. Однако ученые стран арабского Востока совершенно отказались от пользования буквенной символикой. Название неизвестного и его степеней они записывали с помощью специальных слов. Например, неизвестные они называли "вещью"- шай (что потом было переведено на итальянский и получило название "cos a"). Нередко в научных трактатах даже числа записывались не символами (цифрами), а словами. Поэтому-то с точки зрения создания исчисления математика стран арабского Востока ничего не дала.

Другим крупным научным центром была Византия (Константинополь), где хранились, тщательно переписывались и комментировались древнегреческие рукописи.

Из научных центров арабского Востока и Византии начиная с X-XII вв. научная мысль стала проникать в Европу. В XI-XII вв. здесь переводили на латынь Евклида, Архимеда и Аристотеля.

Первым крупным математиком Европы был Леонардо Пизанский (или Фибоначчи) (1180-1240). Он родился в богатом торговом городе - республике Пизе (откуда и происходит добавок "пизанский") и юношей жил в Алжире, где его отец был торговым консулом. Леонардо познакомился с десятичной позиционной системой счисления, принятой у арабов, и с их алгеброй. Он путешествовал по Египту, Сирии, Провансу и Сицилии и, вернувшись домой в Пизу, издал там в 1202 г. книгу "Liber abaci", в которой изложил десятичную позиционную систему и правила арифметических действий в ней, арифметику, геометрию и алгебру. Для своего времени это была замечательная книга, равной которой не появлялось в ближайшие 250 лет.

Достаточно сказать, что в ней решались квадратные уравнения, рассматривались арифметическая и геометрическая прогрессии и был введен и исследован знаменитый ряд Фибоначчи:

члены которого удовлетворяют соотношению:

Однако, ничего не зная о символике Диофанта и его методах, Леонардо не пользовался алгебраическим языком.

В Европе буквенные обозначения для неизвестного и его степеней начали применять только в XV в., после того как пала Византия и греческие ученые переехали на Запад. Но в Византии пользовались не системой обозначений Диофанта, основанной на аддативном принципе, а неудобной системой, описанной у византийского ученого Михаила Пселла (XI в.) и восходящей, по-видимому, к Анатолию, другу и корреспонденту Диофанта. Эта система была основана на мультипликативном принципе, т. е. квадрато-куб означал в ней 6-ю степень, а кубо-куб - 9-ю. 5-я степень, которую нельзя было представить в виде произведения 2α и 3β , называлась "первой невыразимой", 7-я -"второй невыразимой". Приведем для примера обозначения, которые употреблял Лука Пачоли (ок. 1445-ок. 1515) в своей знаменитой книге "Сумма знаний по арифметике, геометрии, отношениям и пропорциям", которая была напечатана в Венеции в 1494 г. (это была первая печатная книга по математике). Вот эта таблица:

Мы видим, что Лука распространил обозначения на первые 29 степеней неизвестного, причем 9 из них оказались "невыразимыми" (relato - это, по-видимому, ошибочный перевод греческого термина α^''λογοζ - "невыразимый", прочитанный как ο'λογοζ - "отношение"). Никаких символов для отрицательных степеней неизвестного у него нет. Зато он вводит обозначения для действий:

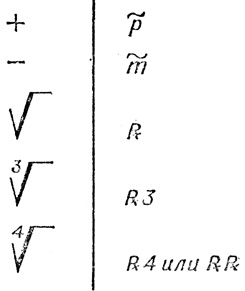
Аналогичные обозначения применяли и так называемые "коссисты" - математики-алгебраисты Германии и Чехии. Наиболее известный из них Иоганн Видман (1460 г.- первая половина XVI в.) ввел для сложения и вычитания знаки + и -, которые быстро вытеснили итальянские обозначения p^- и m^-.

Наконец, Рафаэль Бомбелли (Италия) и Симон Стевин (Нидерланды) ввели новые обозначения для степеней неизвестного, в которых подчеркивалась однородность ряда степеней^*. Например, x, x², x³, ... . Бомбелли обозначал символами 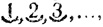а Стевин - Так что многочлен x² - 10x + 5 в записи Бомбелли выглядел так: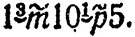

^* (Принцип такого обозначения также содержался у Пселла, который называл x - первым числом, x² - вторым числом, x³ - третьим и т. д.)

Стевин ввел обозначения и для второго неизвестного и его степеней:

а также для третьего:

Однако никому из математиков до Виета (1540-1603) не пришло в голову ввести обозначения для произвольных постоянных величин, входящих в задачу. Поэтому формул, к которым мы так привыкли в математике, до Виета не было.

II. Между тем европейская алгебра в XVI в. добилась первых крупных успехов - были решены в радикалах уравнения 3 и 4 степеней. Эти задачи много веков представлялись неразрешимыми. Еще Лука Пачоли в своей "Сумме" сравнивал их с квадратурой круга.

С решением кубических уравнений была связана целая история, наполненная интригами, коварством и обманом. Мы не будем здесь на ней останавливаться, отсылая любознательных читателей к интересной брошюре С. С. Демидова^*, изданной в этой же серии. Скажем только, что формулы для решения уравнения

были впервые, по-видимому, найдены профессором университета в Болонье Сципионом дель-Ферро (1456-1526), который не публиковал своего открытия, затем вновь в 1535 г. самостоятельно получены Никколо Тартальей (1500-1557), а впервые опубликованы они были в 1545 г. в книге Дж. Кардано "Ars magna" (т. е. "Великое искусство" - этим именем тогда называли алгебру) и с тех пор носят название формул Кардано. Н. Тарталья решил и уравнение вида:

^* (См.: С. С. Демидов. У истоков современной алгебры, М., "Знание", 1971.)

Он пришел к формулам, которые в современных обозначениях выглядят так:

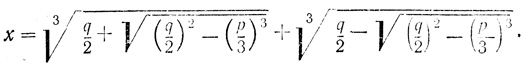(3)

Если (^q/₂)² - (^p/₃)³ < 0, то в формуле (3) под квадратным корнем оказывается отрицательное число, что не позволяло найти корень x уравнения (2). Этот случай получил название "неприводимого". Он послужил камнем преткновения и для Тартальи, и для Кардано.

Читатель может удивиться: ведь и при решении квадратного уравнения

может случиться, что ^b2/₄ - c <0. Какие же новые трудности принесла формула (3)?

Дело в том, что при - ^b2/₄ - c <0 уравнение (4) не имеет действительных корней. Оба корня его будут комплексными сопряженными числами:

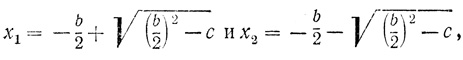
т. е. можно сформулировать следующее ограничение: для того чтобы корни уравнения (4) были действительными, нужно, чтобы

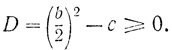
Напротив того, в случае (^q/₂)² - (^p/₃)³ < 0 оказалось, что уравнение (2) имеет действительный корень. И даже три действительных корня! Это можно видеть из примера уравнения

Уравнение (2') имеет корень x = 4.

Два другие его корня можно найти, решая квадратное уравнение:

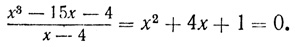
Его корнями будут: x₁ = - 2 + √3 и x₂ = - 2 - √3. Итак, исходное уравнение имеет три действительных корня: 4, -2 + √3, -2 - √3. Между тем (^q/₂)² - (^p/₃)³ = 4 - 125 = -121 <0.

Именно это обстоятельство и смущало математиков XVI в.

Оно же побудило Рафаэля Бомбелли - математика и инженера ввести новые числа.

Рафаэль Бомбелли готовил к изданию свою "Алгебру", когда один из его друзей сообщил ему, что в Ватиканской библиотеке имеется замечательная античная рукопись по алгебре. Ознакомившись с ней, Бомбелли немедленно начал переводить ее, чтобы "обогатить мир произведением такой важности". Эта рукопись являлась списком "Арифметики" Диофанта. Перевод ее Бомбелли так и не закончил, зато в его "Алгебре", опубликованной в 1572 г., появились 143 задачи из "Арифметики" (всего в ней 189 задач), методы решения которых он хорошо усвоил. Извлек он из "Арифметики" и способ введения новых чисел. В своей "Алгебре" он сначала вводит отрицательные числа (meno), которые многими в то время квалифицировались как "ложные". Делает он это тем же способом, что и Диофант, т. е. определяя над ними правила действий при помощи таблицы:

Корень квадратный из отрицательного числа, как замечает Бомбелли, не может быть ни положительным, ни отрицательным числом. Эти "софистические" числа Бомбелли называет "piu di meno", т. е. плюс из минуса (+√(-1))" или "meno di meno", т. е, минус из минуса (-√(-1)) и также вводит их аксиоматически, определяя правила действий с ними:

(т. е. в наших обозначениях (+i) (+i) = -1; (+i) (-i) = +1 и т. д.).

Никакой интерпретации новым числам Бомбелли не дает. Он рассматривает их как формальные символы, о которых ничего неизвестно, кроме правил (5).

С помощью этих чисел Бомбелли удалось разъяснить неприводимый случай.

Если дано уравнение (2'), то

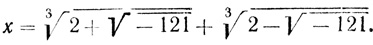
Но как нашел Бомбелли (2 + i)³ = 2 + 11i, т. е.

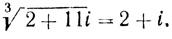
Он знал также, что если

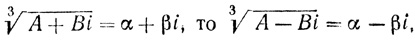
поэтому x = 2 + i + 2 - i = 4 - "мнимые" компоненты уничтожаются и корень оказывается действительным. Это, конечно, не было "решением" уравнения (2) в общем случае, так как алгебраически нельзя найти 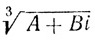, т. е. найти α и β такие, что 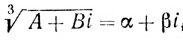, но это объясняло, в чем состоит механизм получения решения.

Заметим, что введенные Бомбелли мнимые числа имели для математики огромное значение, гораздо большее, чем задача, благодаря которой они возникли.

Однако в течение двух столетий мнимые компоненты воспринимались математиками как удобные символы, которые применялись только в промежуточных выкладках, а результат всегда формулировался для "настоящих", т. е. действительных чисел. Лишь в начале XIX в. положение дел изменилось и комплексные числа получили права гражданства, но еще раньше, а именно в творчестве Виета, появилось новое исчисление, "исчисление треугольников", с успехом заменившее оперирование с комплексными числами.

Таким образом, как линия развития алгебраической символики, так и линия развития понятия числа подводит нас к творчеству замечательного французского математика - Франсуа Виета.

III. Франсуа Виет родился в 1540 г. в городе Фонтене-ле-Конт, в 60 км от ла-Рошели - знаменитой крепости гугенотов. Виет был сыном прокурора и сам избрал карьеру юриста. По окончании курса в г. Пуатье он начал заниматься юридической практикой в родном городе. Но уже через четыре года поступил секретарем и домашним учителем к знатному дворянину-гугеноту де-Партеней. Виет занимался с его 12-летней дочерью Екатериной космогонией и очень увлекся изучением астрономии и тригонометрии. Уже в это время, по-видимому, он выразил sin nx и cos nx в виде многочленов от sin x и cos x. После смерти де-Партенея и замужества Екатерины Виет последовал за своей ученицей в Париж. В 1571 г. мы находим его там советником парламента. Вскоре Виет получил видную придворную должность и стал тайным советником королей сначала Генриха III, а затем Генриха IV.

В это время Виет оказал французскому двору крупную услугу. Испания и подвластная ей территория Нидерландов были разделены враждебной Францией. Переписка с Нидерландами велась с помощью особого шифра, который содержал более 500 знаков. Эти знаки к тому же время от времени изменялись. Французы часто перехватывали письма в Нидерланды, но долгое время не могли их расшифровать. Только когда это дело поручили Виету, он быстро нашел ключ к шифру, и в течение двух лет французы знали о всех планах и сложных интригах испанского двора. Впоследствии испанцы обвиняли Генриха IV в том, что на его службе находится дьявол.

Виет жил в эпоху кровопролитных религиозных войн.

Вопрос о том, был ли сам Виет католиком или гугенотом, остается темным. Нам известно только, что его связь со знатными и активными деятелями-гугенотами (первый муж Екатерины Партеней был убит в Варфоломеевскую ночь, второй - принц де-Роган - являлся одним из признанных гугенотских вождей, сама Екатерина играла видную роль при защите ла-Рошели) привела к тому, что по настоянию ярых католиков-герцогов Гизов Виет был отстранен от должности в конце 1584 г. и вновь приглашен ее занять в начале 1589 г. (после разрыва короля с Гизами). Эти четыре года оказались чрезвычайно плодотворными для творчества Виета. Все это время он работал над большим трудом "Искусство анализа" или "Новая алгебра". Рассказывают, что Виет, работая, мог просиживать за письменным столом по трое суток подряд, иногда только подпирая голову рукой и забываясь сном на несколько минут. И все же труд не был завершен.

Но главное было написано. И это главное переделало всю математику Нового времени.

В 1646 г. сочинения Виета были собраны его учениками и изданы в Лейдене. Первые два из этих сочинений, носящие заглавия

1. "Введение в аналитическое искусство" (In artem analiticem Isagoge.)
2. "Предварительные замечания к видовой логистике" (Ad logisticam speciosam notae priores.),

и будут нас здесь интересовать.

В первом из них Виет ставит своей целью создать новую алгебру, т. е. такое аналитическое искусство, которое обладало бы строгостью геометрии древних, но позволяло бы "хорошо производить математические операции". С этой целью он делит все величины на "ступени"; К первой из них относятся "длины" или величины одного измерения, их можно между собой складывать и вычитать из большей меньшую. Произведение двух величин 1-й ступени принадлежит уже 2-й ступени, которая содержит "площади" или величины двух измерений.

Мы видим, что в этом Виет следовал "геометрической алгебре" древних. Но Виет рассмотрел бесконечно много "ступеней". Если обозначить множество величин n-й ступени Виета через Rⁿ₊ то множество всех его величин будет:

Для величин, принадлежащих одной и той же ступени Rⁿ₊, определены сложение и вычитание меньшей величины из большей. Если же α∈Rⁿ₊ и β∈R^m₊, то для них определено умножение и αβ∈R^m+n₊. Если n>m, то определено и деление, причем αβ∈R^n-m₊.

Все величины этих "ступеней" Виет обозначил согласными буквами алфавита: B, C, D. Неизвестные, которые тоже располагаются по ступеням (к Rⁿ₊ принадлежат n-е степени неизвестных), он обозначил гласными буквами: A, E, I.

Таким образом, он построил первое буквенное исчисление, которое, однако, отличалось от современного. Для составления уравнений, например, нужно было соблюдать "принцип однородности", т. е. следить, чтобы все его члены принадлежали одной и той же ступени. Например, уравнение

в записи Виета выглядело бы так:

"B plano" означает, что B∈R²₊, а "D solido", что D∈R¹₊.

Итак, это первое буквенное исчисление дало возможность записывать уравнение с произвольными буквенными коэффициентами, а также записывать и выводить алгебраические тождества.

Выводу необходимого запаса формул-тождеств посвящено второе сочинение. Там, например, выводятся соотношения:

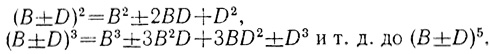
Было ли это существенно?

Мы уже говорили, что основное преимущество символов состоит не только в том, что они позволяют сократить запись, а главным образом в том, что для них могут быть определены математические операции, сложения, вычитания, умножения, деления, для них можно определить правила раскрытия скобок и подстановок. Поэтому-то буквенное исчисление позволяет заменить часть мыслительных операций чисто механическими вычислениями. А такая "механизация" мыслительных операций делает уже возможным замену их работой машины.

IV. Последняя часть "предварительных замечаний к видовой логистике" носит название "Порождение треугольников" (Genesis triangulorum). В нем как раз и строится исчисление треугольников, эквивалентное оперированию с комплексными числами.

В основе "исчисления треугольников" лежит формула, известная еще Диофанту:

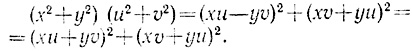
Из нее Диофант выводил, что если некоторые числа p и q представимы суммами двух квадратов, то их произведение будет представимо в том же виде двумя различными способами. Например: 5 = 1² + 2², 13 = 2² + 3².

Эту формулу в общем виде доказал Леонардо Пизанский в своей "Книге квадратов" (12225).

Виет выводит формулу алгебраически, пользуясь своим буквенным исчислением, а затем ставит задачу: из двух прямоугольных треугольников с рациональными сторонами составить третий, у которого все стороны рациональны, а гипотенуза равна произведению гипотенуз составляющих треугольников.

если первый составляющий треугольник имеет стороны (x, y, z), где x - основание, y - высота, а z - гипотенуза, а второй - стороны (u, v, w), то из них можно составить два новых прямоугольных треугольника, удовлетворяющих условию задачи:

1. (|xu - yv|, xv + yu, zw);
2. (xu + yv, |xv - yu|, zw) (рис. 9).

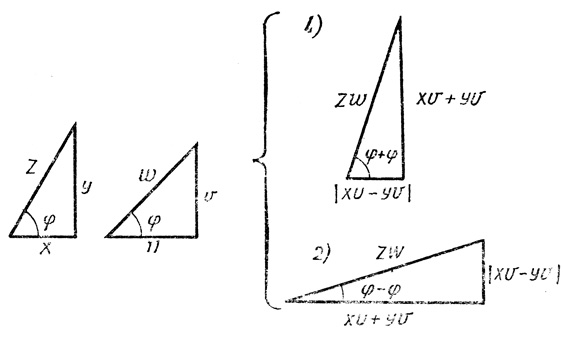
Рис. 9

Виет отмечает, что если φ - острый угол при основании треугольника (x, y, z), а ψ - острый угол при основании треугольника (u, v, w), то угол при основании первого составного треугольника будет φ + ψ, а второго - φ - ψ (в предположении, что φ + ψ<^π/₂, φ - ψ > 0).

Композицию треугольников Виета можно интерпретировать как операцию умножения комплексных чисел. Поставим в соответствие прямоугольному треугольнику (x, y, z) комплексное число α = x + iy, причем |α|² = x² + y², Arg α = φ. Тогда первая операция Виета равносильна перемножению чисел α = x + iy и β = u + iv, (|β|² = u² + v², Arg β = ψ):

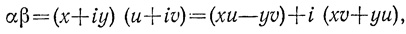
причем |αβ|² = |α|², |β|² = z²w², т. е. произведению чисел αβ отвечает первый составной треугольник Виета (|xu - yv|, xv + yu, zw). Как отмечает Виет, Arg (αβ) = Arg α + Arg β.

Что же соответствует второй операции Виета? Легко видеть, что это будет произведение α и числа сопряженного β, т. е.

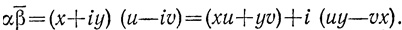
Это отвечает треугольнику (xu + yv, |uy - vx|, zw). Причем Arg (αβ^-) = Arg α + Arg β^- = Arg α - Arg β. Таким образом, не вводя явно никаких "мнимостей", Виет построил исчисление, эквивалентное исчислению комплексных чисел.

Виет применил это исчисление для получения треугольника, получающегося n-кратным умножением треугольника α = (x, y, z) самого на себя, иначе говоря, для вывода формулы (x + iy)ⁿ. Виет последовательно находит^*:

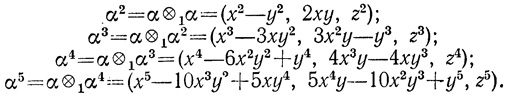
^* (Здесь Φ₁ - композиция, соответствующая первой операции Виета.)

Затем он формулирует общее правило: для определения основания и высоты треугольника αⁿ, полученного n-кратным умножением α = (x, y, z) на себя, необходимо, образовать n-ю степень бинома x + y и "полученные отдельные однородные члены последовательно разделить на две части, и в обеих первые члены взяты положительными, а затем отрицательными" и т. д.; тогда "первая часть будет подобна основанию (искомого) прямоугольного треугольника, а вторая - высоте. Гипотенуза же подобна той же степени гипотенузы (исходного) прямоугольного треугольника".

Треугольник α = (x, y, z) Виет называет треугольником угла φ = Arg (x + iy), α² (имеет двойной угол при основании)- треугольником угла 2φ, α³ - 3φ, α⁴ - 4φ и т. д.

Итак, Виет предлагает следующую процедуру: надо возвести бином x + y в n-ю степень:

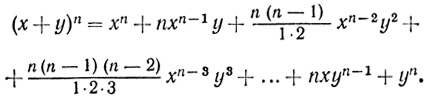
Тогда

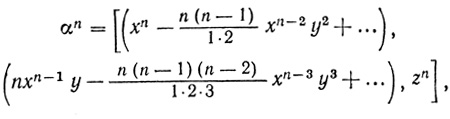
что в точности отвечает нашей формуле:

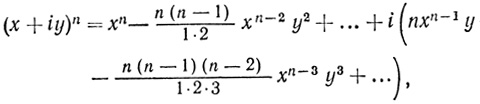
в которой сгруппированы действительные, а затем чисто мнимые члены.

Но Виет на этом не останавливается. Он замечает, что каждый из треугольников α², α³, ... может быть охарактеризован острым углом при основании 2φ, 3φ, ... и гипотенузой, т. е. α² = (z², 2φ), α³ = (z³, 3φ), ...

Основание n-го треугольника x_n = zⁿ*cos nφ, а высота y_n = zⁿ*sin nφ, или в современных обозначениях

^* (Это и есть так называемая формула Муавра (XVIII в))

Одновременно он получает формулы для выражения cos nφ и sin nφ через степени cos φ и sin φ.

V. Свое "исчисление" Виет применил для решения задач Диофанта и для исследования "неприводимого" случая.

В задаче 9 книги II Диофант рассматривает уравнение

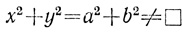
и решает его для a = 2, b = 3. Для этого он делает подстановки

Тогда

или

при k = 2, t = 8/5, x = 18/5, y = 1/5.

Виет уже знал это решение и воспроизвел его в своем сочинении "Зететика" (так Виет называл учение о решении уравнений), но после этого привел и другое решение:

пусть (p, q, r) - прямоугольный треугольник с целыми рациональными сторонами, т. е.

(например, (3, 4, 5) или (5, 12, 13). Виет применяет к этому треугольнику и к треугольнику (a, b , √(a² + b²) свои композиции ⊗₁ и ⊗₂:

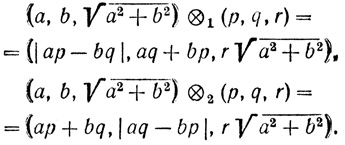
Затем Виет берет треугольник, подобный полученному, с гипотенузой r. Его катеты будут в первом случае:

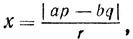
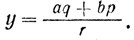
а во втором:

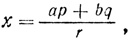
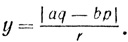
И в обоих случаях x² + y² = a² + b².

По существу, Виет применяет здесь композицию к треугольникам (a, b, √(a² + b²) и (^p/_r, ^q/_r, 1), т. е. с нашей точки зрения правило умножения числа α = a + bi на число β = ^p/_r + ^q/_ri модуль которого |β| = 1.

Тогда

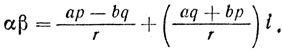
Виет показывает, что оба способа решения приводят к одинаковым результатам.

Что касается исследования "неприводимого" случая, то идея Виета состояла в сведении его к задаче трисекции угла. Пусть дано уравнение

пусть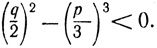

Его всегда можно представить в виде:

а так как (^ar2/₂)²<r², то a²<4r² и a<2r, поэтому а можно всегда записать так: a = 2r sin u. Тогда x = 2r sin ^u/₃, т. е. уравнение сведется к уравнению трисекции угла, которое получается из способа возведения α = (cos φ, sin φ, 1) в 3-ю степень. Нетрудно видеть, что

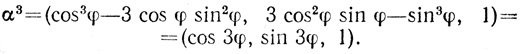
Отсюда sin 3φ = 3 cos² φ sin φ - sin³ φ.

Или, обозначая sin φ = x, 3φ = u, получим: sin u = 3x - 4x³, т. е. 2 sin u = 3 (2x) - (2x)³.

Обозначая далее 2x = -y, 2 sin u = a, найдем y³ = 3y + a. Отсюда видно, что все три корня в этом случае - вещественные.

Аналогичным методом Виет решил и знаменитую задачу нидерландца Адриана ван Роумена, посланную им в виде вызова математикам всего мира. Рассказывая об этом вызове королю Генриху IV, нидерландский посланник добавил, что к французским математикам ван Роумен не обращается, так как таковых во Франции, видимо, нет.

"И все же,- возразил король,- у меня есть математик и весьма выдающийся. Позовите Виета". Виет прочел письмо ван Роумена, в котором требовалось решить уравнение

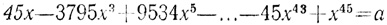
при

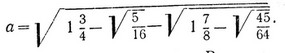
Сохранились сведения о том, что Виет сразу же нашел один корень, а на следующее утро представил еще 22 решения этого уравнения.

Виет увидел, что предложенное а является стороной вписанного в круг правильного 15-угольника, т. е. является хордой, стягивающей дугу в ^360°/₁₅ = 24°. Коэффициенты при x⁴⁵, x⁴³, ..., x показывали, что дело идет о делении этого угла на 45 равных частей, т. е. одним из решений будет:

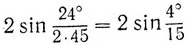
Остальные положительные решения будут иметь вид:

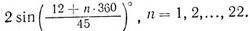
Оставшиеся еще 22 решения будут отрицательными, поэтому Виет их не учитывал.

Ответ Виета был опубликован в 1594 г. (на следующий год после постановки задачи) и принес ему мировую славу.

Буквенное исчисление Виета было первым, позволившим заменить часть мыслительных операций механическими. С этих пор в математику входят формулы. Сначала, как мы видели, это было сделано в алгебре, но вскоре буквенное исчисление было построено и в математическом анализе, а именно, дифференциальное и интегральное исчисление, которое в XVII в. часто называли алгеброй бесконечного. Теперь имеются исчисления, специально построенные для геометрии (векторное и тензорное), исчисления высказываний и предложений в математической логике и многие другие, создаваемые специально для нужд тех или иных математических и даже технических задач.