2. Геометрическая алгебра Древней Греции

I. VI-V вв. до н. э. ознаменовались для Греции великими событиями: там впервые в истории человечества было создано демократическое государство, возникли трагедия и комедия и, наконец, была создана математика как абстрактная теоретическая наука.

Каждое из этих событий имело неоценимое значение для всей истории и культуры человечества, а появление всех трех граничило с чудом. Оно и получило название "греческого чуда".

Нам здесь особенно важно, что именно в это время возникла математика как абстрактная наука, основанная на системе доказательств. Такое преобразование математической науки из рецептурной, какой она была в Египте и Вавилоне, в доказательную произошло, как утверждают все античные авторы, в школе Пифагора, который около 530 г. до н. э. переехал с острова Самос, своей родины, в Кротон (Южная Италия), где и основал пифагорейский союз - братство, преследовавшее политические, морально-этические и научные цели.

Знаменитый философ - неоплатоник Прокл (V в. н. э.) в своих комментариях к "Началам" Евклида писал: "...Пифагор преобразовал эту мудрость (т. е. математические знания.- И. Б.) в форму свободного учения. Он рассматривал начала геометрии абстрактным образом и получал ее теоремы не материальным, а интеллектуальным способом.

Это он открыл учение об иррациональностях и построении космических тел".

Систематическое введение доказательств в математику стимулировало ее быстрое развитие. В Греции V-III вв. до н. э. были созданы первые математические теории: построены система евклидовой геометрии, элементарная теория чисел, теория конических сечений (т. е. кривых 2-го порядка), первая теория действительных чисел и элементы теории пределов.

Здесь уместно будет сказать несколько слов о роли доказательств в нашей науке. Обычно говорят, что доказательство служит для установления истинности того или иного математического предложения. Это, конечно, верно. Но дело не только в этом. Доказательства выявляют связи между математическими предложениями, позволяют установить, от каких посылок это предложение зависит. Так, например, предложения "внешний угол треугольника больше каждого внутреннего, с ним не смежного" и "сумма углов треугольника равна 2d", которые при первом знакомстве кажутся сходными, на самом деле зависят от совершенно различных посылок. Первое из них не зависит от аксиомы параллельности, оно верно в так называемой "абсолютной геометрии" (оно верно и в геометрии Лобачевского), а второе существенно зависит от аксиомы параллельности и в геометрии Лобачевского не имеет места. Таким образом, доказательства дают нам возможность классифицировать и "упорядочивать" математические предложения. Поэтому некоторые особенно важные предложения имеют иногда много различных доказательств (так, Гаусс дал 8 различных доказательств квадратичному закону взаимности, а теперь их известно более 40). Ученые ищут новые доказательства не потому, что сомневаются в старых, а потому, что хотят найти наиболее "естественные" доказательства или установить связи рассматриваемой теоремы с другими частями математики.

Но вернемся к "ранним" пифагорейцам (т. е. жившим в VI - начале V в. до н. э.). Никаких текстов от них не дошло. Кроме того, по традиции они приписывали все свои открытия "самому", т. е. Пифагору, о котором уже при жизни ходили загадочные легенды. Кто на самом деле был автором ранних теорий, узнать нельзя, поэтому мы будем говорить о "математике пифагорейцев", пользуясь сведениями, которые можно почерпнуть из сочинений Платона и Аристотеля, а также из отрывков трудов математиков-пифагорейцев конца V в. до н. э., таких, как Архит из Та-рента и Феодор из Кирены.

Пифагорейцы делили математику на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке). При этом, как свидетельствует Архит, "первой" из них была арифметика; она лежала в основе и геометрии, и астрономии, и гармонии.

Числом пифагорейцы называли "множество единиц", т. е. числами они признавали только целые положительные (или натуральные) числа. Единица E была материей чисел, она считалась неделимой, поэтому ни о каких "частях" ее ^m/_n E говорить было нельзя. Дроби осмысливались в теоретических сочинениях как "отношение чисел", вместо того чтобы говорить о ^m/_n E, они рассматривали отношение двух целых чисел - mE : nE. Таким образом возникла первая теория "пар чисел". По существу, это означало, что в арифметику были введены положительные рациональные числа.

Пифагорейцы первоначально полагали, что рациональных чисел достаточно для обоснования учения о подобии. Они считали, что все отрезки соизмеримы, поэтому, если надо найти отношение отрезков AB и CD, то надо найти их общую меру F, Тогда AB = pF, CD = qF и AB : CD = pF : qF = p : q.

В гармонии пифагорейцы также обнаружили, что "созвучными" будут музыкальные интервалы, отвечающие струнам, длины которых имеют отношение 1:2 (октава), 2:3 (квинта), 3:4 (кварта). Эти открытия привели пифагорейцев к мысли, что "все есть число", что все закономерности мира можно выразить с помощью целых чисел и их отношений. Вот что об этом писал Аристотель:

"Так называемые пифагорейцы были первые, занимавшиеся науками (τα ματη'μααα). Поскольку в дальнейшем они узнали, что отношения и законы музыкальной гармонии основываются на числах, а также все остальные (предметы) походят на числа... то они высказали мнение, что элементы чисел являются элементами всех вещей и что весь мир в целом является гармонией и числом" (Аристотель "Метафизика А5, 985в").

Платон в "Государстве" пишет, что арифметика есть "учение о четных и нечетных числах". Отрывок из этого древнего учения содержится в IX книге "Начал" (предл. 21-34). Ко времени Евклида было уже доказано, что произведение двух целых чисел AB тогда и только тогда может делиться на простое число p, если по крайней мере один из сомножителей A или B делится на p. Исходя из этой теоремы, можно доказать, что любое натуральное число N однозначно представимо в виде произведения простых:

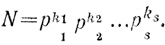
Пифагорейцы доказали аналогичные теоремы не для любого простого числа p, а для наименьшего простого, т. е. для p = 2. Они доказали, что произведение AB может быть четным (т. е. делиться на 2) тогда и только тогда, если по крайней мере одно из чисел A или B - четно. Отсюда следовало, что каждое целое N однозначно представимо в виде:

где N₁ - нечетно. Исходя из своего учения, пифагорейцы находили "совершенные числа", т. е. равные сумме своих делителей. Они доказали, что если 1 + 2 + ... + 2ⁿ = p - простое, то 2ⁿp будет числом совершенным. Так, при n = 1, p = 3, 2p = 6 - совершенное, при n = 2, p = 7 - простое, значит 2²*7 = 28 - совершенное и т. д.

В XVIII в. великий математик Леонард Эйлер доказал, что никаких других четных совершенных чисел, кроме найденных пифагорейцами, не существует.

Но эта первая "арифметизация" математики вскоре потерпела крах. В самой пифагорейской школе было сделано открытие, показывающее, что существуют "несоизмеримые отрезки", т. е. такие, отношение которых не может быть выражено с помощью целых чисел.

Первыми найденными отрезками такого рода были сторона и диагональ квадрата. Аристотель писал: "Если бы сторона и диагональ квадрата были соизмеримы, то нечетное число равнялось бы четному".

В "Началах" Евклида в конце X книги имеется доказательство, в точности соответствующее словам Аристотеля. Оно опирается на "теорему Пифагора", которую умели доказывать пифагорейцы, и на "учение о четных и нечетных".

Вкратце воспроизведем это наиболее древнее известное нам доказательство.

Пусть АВГΔ - квадрат и пусть сторона и диагональ его соизмеримы (рис. 2):

где m и n не являются оба четными, иначе их можно было бы сократить на 2. Из (1) следует, что

Рис. 2

Но по теореме Пифагора (АГ)² = 2(АВ)², следовательно,

значит m² - четно. Из учения о четных и нечетных следует, что в этом случае и m - четно (так как произведение двух нечетных чисел нечетно). Но тогда n - нечетно. Поскольку m - четно, то m = 2t. Подставляя m в (2), получим: 4t² = 2n², или n² = 2t², т. е. n² - четно, следовательно, и n должно быть четным, что приводит к противоречию.

Открытие несоизмеримости означало, что целых чисел и их отношений недостаточно для выражения отношений любых двух отрезков, что с помощью одних только рациональных чисел нельзя строить метрическую геометрию. Это-то и поразило греков.

В диалоге Платона "Законы" афинянин говорит, что поздно узнал о несоизмеримости и что до этого он был подобен неразумному животному. Аристотель писал в "Метафизике": "...Все начинают с изумления, обстоит ли дело именно так, как "недоумевают", например, про загадочные самодвижущиеся игрушки, или "сходным образом" в отношении солнцеворотов, или несоизмеримости диагонали; ибо у всех, "кто еще не рассмотрел причину", вызывает удивление, если что-нибудь нельзя измерить самою малою мерою".

Вскоре были найдены и другие несоизмеримые отрезки. Так, согласно Платону, Феодор из Кирены показал, что стороны квадратов с площадями 3, 5, 6, 7, 8, 10, 11, 12, 13,14,15 несоизмеримы со стороной единичного квадрата, а его юный высокоодаренный ученик - Теэтет доказал, что если площадь квадрата выражается любым целым неквадратным числом N, то сторона его несоизмерима с единицей. Иными словами, было установлено, что если N ≠ α², то √N не выражается никаким рациональным числом, что он - иррационален.

Итак, целых чисел и их отношений оказалось недостаточно для выражения отношений геометрических величин. Арифметика в том виде, в каком она была в то время, не могла служить основой для геометрии.

Какой же мог быть выход из создавшегося кризиса? Расширить числовую область? На той ранней стадии развития математики это вряд ли было возможно. Но как же быть? Может быть, вовсе отказаться от построения абстрактной науки, которая преподносит такие странные сюрпризы? Но и этого пифагорейцы делать не хотели: слишком прекрасными и стройными были их теории.

И вот, пифагорейцы пришли к мысли, что поскольку геометрические величины имеют более общую природу, чем числа, то в основу математики надо положить не арифметику, а геометрию. Это был настоящий революционный переворот, который на первых порах принес богатые плоды. Геометрическое облачение придало всей классической греческой математике необыкновенную красоту и монолитность. При этом и учение о решении уравнений, да и сама арифметика приобрели геометрическую форму. "Геометрическая алгебра" нам хорошо известна, так как она изложена во II и частично в I книгах "Начал" Евклида. Сейчас мы дадим о ней представление и нашим читателям.

II. "Геометрической алгеброй" мы теперь называем ту часть античной математики, в которой было построено прямое исчисление отрезков и площадей.

Сложение отрезков осуществлялось геометрически - путем приставления одного, к другому, вычитание - путем выкидывания из большего отрезка части, равной меньшему. Операция вычитания была возможна лишь тогда, когда вычитаемое не превосходило уменьшаемого. Произведением двух отрезков назывался построенный на них прямоугольник. Разумеется, не имело смысла говорить о сложении прямоугольника и отрезка. Поэтому исчисление, определенное в геометрической алгебре, было "ступенчатым". Первую ступень составляли отрезки, вторую - площади, которые обычно задавались в виде треугольников или прямоугольников, третью - объемы.

Это позволило впервые в истории устанавливать в общем виде алгебраические тождества. Так, тождество

было установлено с помощью фигуры, изображенной на рис. 3, в которой AE = a, а BE = b.

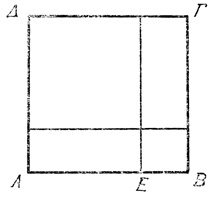
Рис. 3

Справедливость тождества была этим установлена для любых a и b независимо от их конкретных величин и независимо от того, являются ли- они соизмеримыми или нет.

С помощью "геометрической алгебры" стало возможным изучение общих свойств алгебраических операций.

Так, в I предложении II книги Евклид доказывает, что прямоугольник, заключенный между двумя отрезками, будет равен сумме прямоугольников, заключенных между одним из этих отрезков и прямыми, параллельными ему и рассекающими прямоугольник на части (рис. 4).

Рис. 4

Таким образом, если a = a₁ + a₂ + a₃, то ba = b(a₁ + a₂ + a₃) = ba₁ + ba₂ + ba₃.

С нашей точки зрения, это предложение устанавливает закон дистрибутивности умножения по отношению к сложению. Удивительно, что еще в III в. до н. э. Евклид заметил этот закон и счел необходимым его обосновать!

Задачи, эквивалентные квадратным уравнениям, формулировались как задачи на "приложение площадей". Первая из них гласила: приложить к данному отрезку а заданную площадь S так, чтобы "недостаток" был квадратом.

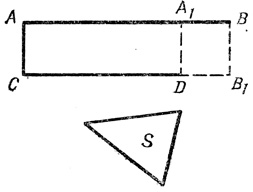
Рис. 5

Пусть AB = a и S - площадь, заданная в виде треугольника (рис. 5). Надо было "приложить" S к AB так, чтобы AA₁DC = S, а прямоугольник ABB₂D - "недостаток" - был квадратом. Если обозначить A₁B = x, то задаче будет отвечать уравнение:

По-гречески "недостаток" называется словом "эллейпсис", поэтому такое приложение площадей получило название эллиптического.

Заметим, что древне рассматривали уравнение эллипса относительно его вершины^*, т. е. в наших обозначениях оно имеет вид:

поэтому и соответствующая кривая получила название эллипса.

^* (Аполлоний записывал это уравнение геометрически - с помощью геометрической алгебры.)

В "Началах" отмечается, что задача возможна при 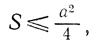поскольку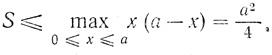

Другая задача была двойственна первой: приложить к данному отрезку а данную площадь 5 так, чтобы "избыток" был квадратом. Эта задача эквивалентна решению уравнения:

"Избыток" по-гречески будет "хиперболе", поэтому и задача получила название гиперболической (отсюда же и название гипербола для кривой y² = kx (a + x)).

К двум рассмотренным нами задачам добавлялась еще третья: преобразовать данный прямоугольник ab в квадрат x², т. е. требовалось решить уравнение:

Решение всех трех задач основывалось на преобразовании произведений ab, x (a - x) и x(a + x) в разность двух квадратов, для чего применялось тождество:

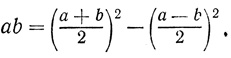
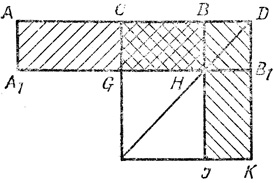
Рис. 6

Оно устанавливалось геометрически (см. рис. 6). Пусть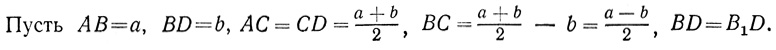

Тогда, как нетрудно видеть, прямоугольник ABMA₁ равновелик "гномону" (угольнику), получающемуся, если из квадрата на CD вычесть квадрат на CB. Действительно, прямоугольники ACC₁A₁ и BDKJ равны между собой, а часть CBMC₁ - общая обеим фигурам (на рисунке она заштрихована дважды).

Таким образом, x² записывался с помощью разности квадратов:

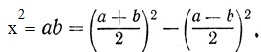
Геометрически x представлялся в виде катета прямоугольного треугольника с гипотенузой ^{a + b}/₂ и другим катетом ^{a - b}/₂. Такой треугольник было нетрудно построить, проводя из С, как из центра окружность радиусом AC (рис. 7), и восстанавливая из B перпендикуляр BJ к AD.

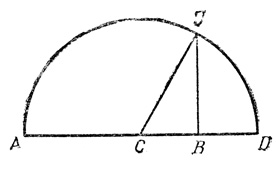
Рис. 7

Так как (BJ)² = (CJ)² - (СВ)² = (АС)² - (СВ)² = 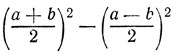, то = BJ.

Зададимся теперь вопросом: какой класс задач можно было решать с помощью "геометрической алгебры"?

Нетрудно видеть, что "разрешимыми" этим методом будут те и только те задачи, которые можно свести к последовательному решению конечного числа квадратных уравнений. Так, например, ребро правильного додекаэдра a = ^D/₆ (√15 - √13) может быть получено в результате решения уравнений:

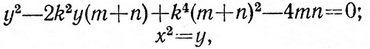
где D - диаметр описанной сферы, k = ^U/₆, m = 15, n = 13.

И наоборот, всякая задача, которую можно решить построением с помощью циркуля и линейки, сводится к последовательному решению квадратных уравнений.

Действительно, все такие построения состоят из следующих элементов: проведение прямой через две точки, нахождение точек пересечения двух прямых, прямой и окружности, двух окружностей. Как нетрудно видеть, все эти точки пересечений можно найти в результате решения либо линейного, либо квадратного уравнений.

Пусть исходные величины лежат в некотором поле_* К. Решение линейного уравнения не выведет нас из этого поля. А вот при решении квадратного уравнения

мы получим, вообще говоря, величины, не принадлежащие исходному полю:

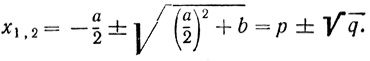
^* (Полем называется множество, замкнутое относительно четырех арифметических действий: сложение, умножение, вычитание и деление, обладающих обычными свойствами.)

Наименьшим полем, содержащим корни уравнения (1), будет поле, состоящее из величин r + s√q, где r, s, q ∈ К. Пусть это наименьшее поле будет K₁ = K (√q).

При дальнейших построениях мы будем оперировать уже величинами из K₁. Если нам снова придется решать квадратное уравнение

то корни его x_1,2 = p₁ ± √q₁.

уже, вообще говоря, не лежат в K₁. Величины r₁ + s₁√q₁, где r₁, s₁, q₁ ∈ K₁ составят новое поле - K₂, минимальное из полей, содержащих корни уравнения (2), и т. д. Таким образом, каждому построению в геометрии Евклида будет отвечать конечная цепочка квадратных уравнений (линейные можно не учитывать):

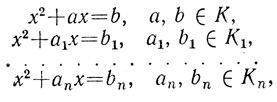
причем коэффициенты каждого последующего уравнения принадлежат полю, содержащему корни предыдущего.

Таким образом, задачи, сводящиеся к решению одного или нескольких квадратных уравнений, и геометрия циркуля и линейки связаны между собой самым тесным образом.

Однако уже в V в. до н. э. в греческой математике появились задачи, которые не могли быть решены средствами классической геометрической алгебры. Иными словами, появились первые "неразрешимые" задачи. Обычно их насчитывают три и называют знаменитыми задачами древности: задачи удвоения куба, трисекции угла и квадратуры круга. Все три задачи имеют очень длинную историю: две из них были решены лишь в 30-х годах XIX в., а третья - только в конце его. Впоследствии к этим задачам была присоединена и четвертая: узнать, какие многоугольники с простым числом сторон могут быть построены циркулем и линейкой? Древние умели строить правильные 3- и 6-угольники. Вопрос состоит в том, чтобы узнать, можно ли построить правильный 7-угольник, а если нет, то существуют ли еще правильные многоугольники, которые допускают построен не циркулем и линейкой? Ответ на этот вопрос был получен только в самом конце XVIII в. молодым К. Ф. Гауссом.

Рассмотрим подробно первую из знаменитых задач. Она формулируется так: построить куб, объем которого был бы в 2 раза больше объема заданного куба, или в наших обозначениях: x³ = 2a³.

Задача эта была настолько популярной, что о ней сложили легенду. Рассказывали, что на острове Делос вспыхнула чума. Оракул, спрошенный о том, как избавиться от этого бедствия, ответил, что надо увеличить вдвое жертвенник, имевший форму куба. Поэтому задача об удвоении куба,носит еще название делосской.

Естественно, что удвоение куба пытались осуществить с помощью того алгоритма, который уже имелся, т. е. с помощью построений циркулем и линейкой. В переводе на язык алгебры это означало, что ³√2 пытались представить в виде конечной комбинации квадратных корней. Это сделать не удавалось. Тогда началось тщательное исследование задачи. Гиппократ Хиоский (V в до н. э.) обобщил ее и свел к отысканию двух средних пропорциональных между заданными величинами. Пусть задан прямоугольный параллелепипед a²b (всегда можно предполагать, что основание уже преобразовано в квадрат), требуется преобразовать его в куб: x³ = a²b.

Решение задали, как показал Гиппократ, эквивалентно нахождению таких двух величин x и y, что

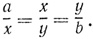
Если b = 2а, то x как раз равняется ребру удвоенного куба. Вскоре Архит из Тарента показал, что эти величины можно найти, рассмотрев пересечение трех поверхностей: тора (у которого внутренний круг имеет нулевой радиус), конуса и цилиндра. Это решение скорее доказывало существование двух средних между любыми двумя величинами, чем давало эффективный способ их нахождения. В существовании поверхностей, полученных вращением окружностей и скольжением прямых по окружности, древние не сомневались. Пересечение таких поверхностей и давало решение. Дальнейшие попытки ученых были направлены к нахождению способа построения двух средних между двумя заданными величинами. Для этого обратились к тем геометрическим местам, которые получаются из пропорции Гиппократа:

Пересечение этих двух "мест" и давало решение задачи. Однако исследование "мест" было делом отнюдь нелегким. Прежде всего надо было установить, являются ли эти "места" непрерывными кривыми (тогда можно говорить о точке их пересечения) или представляют дискретный ряд точек. Только Менехму (вторая половина IV в. до н. э.) удалось представить эти "места" как плоские сечения конусов вращения. Менехм рассмотрел три рода конусов вращения: прямоугольные конуса, тупоугольные и остроугольные. Проводя сечения плоскостью, перпендикулярной к образующей, он получил три рода кривых, которые мы теперь называем соответственно параболой, гиперболой и эллипсом. Эти названия кривым дал Аполлоний (III в. до н. э.). До этого их так и называли сечениями прямоугольного, тупоугольного и остроугольного конуса. После такого стереометрического определения Менехм переходил к выводу планиметрических свойств полученных сечений и в дальнейшем оперировал только с этими планиметрическими свойствами, равносильными нашим уравнениям (например, py = x² для параболы).

Для чего же нужно было это стереометрическое определение? По-видимому, как и в решении Архита, оно служило для доказательства существования и непрерывности рассматриваемых геометрических мест^*.

^* (Эта точка зрения была впервые высказана известным датским историком науки Г. Г. Цейтеном.)

Итак, исследование задачи удвоения куба, которая сама по себе является весьма частной, привело к введению в математику новых чрезвычайно важных кривых - конических сечений. Эти кривые были всесторонне изучены уже в античности и являлись там основными геометрическими объектами наряду с прямыми и окружностями. Архимед изучал тела, полученные вращением конических сечений, и определял их объемы. Он же систематически применял конические сечения для решения задач, эквивалентных кубическим уравнениям. Так, для решения задачи, эквивалентной уравнению

Архимед рассмотрел гиперболу, которая в наших обозначениях имеет уравнение y = ^S/_{a - x} и параболу y = ^x2/_b. Корни уравнения (3) он получил как абсциссы точек пересечения этих кривых (рис. 8). При этом он исследовал уравнение и нашел условия того, чтобы парабола пересекала гиперболу в двух точках (положение I), касалась ее в одной точке (положение II) и не имела с ней ни одной общей точки при 0≤x≤a (положение III).

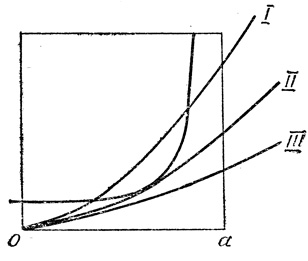
Рис. 8

Уже простейшее кубическое уравнение, как мы видим, не могло быть решено средствами геометрической алгебры.

Уравнение степени n≥4 нельзя было даже представить непосредственно с помощью равенств площадей или объемов. Здесь приходилось прибегать к "обходному пути", привлекая сложный и неудобный аппарат пропорций. Кроме того, геометрический язык был тормозом для расширения понятия числа. В геометрической алгебре не было места для отрицательных чисел, не говоря уже о мнимых.

Таким образом, геометрическая алгебра, позволившая на первых порах получить большие тактические преимущества перед числовой алгеброй Вавилона (доказательство тождеств, общее решение квадратных уравнений и исследование их), при дальнейшем развитии математики сделалась помехой. Она, подобно панцирю, сковывала живой организм математики и не позволяла ему правильно расти. Можно сказать, что если с точки зрения тактики она и была полезна, то с точки зрения стратегии означала некое тупиковое направление.

Для дальнейшего развития всей математики, в том числе и самой алгебры, необходимо было отказаться от геометрического языка и искать новый более общий и более гибкий. Правильный путь, ведущий к построению такого языка, был найден в первые века нашей эры, о чем мы и расскажем в следующем очерке.