
1. Алгебра Древнего Вавилона
I. В середине прошлого века из Мессопотамии во Францию и Британию начали поступать глиняные таблички, покрытые вытесненными на них клиньями, или "клинописью". В 1849-1850 гг. в развалинах древнего города Ниневии Лейярд нашел дворцовую библиотеку, а в 1853 г. Хормузд Рассам открыл библиотеку Ашшурбанипала. 20 000 табличек из этих раскопок хранятся сейчас в Британском музее. С тех пор таблички поступали в музеи сотнями и тысячами, и теперь их насчитывается около 500 000. Правда, большинство из табличек оказались разрозненными в результате спекуляции ими, которой занимались как местные жители, так и приехавшие со всех концов мира авантюристы. Так что работа ученых над табличками чрезвычайно затруднилась. Начало одного текста может теперь храниться в Лондоне, середина - в Нью-Йорке, а конец - в Париже. Расшифровка текстов шла медленно.
Оказалось, что среди табличек имеются и "математические". Они были расшифрованы только в 1929-1930 гг. Это открыло неведомый до того мир древней математики Двуречья. Здесь особые заслуги принадлежат О. Нейгебауеру, работа которого, появившаяся в 30-х годах нашего столетия, положила начало бурному потоку исследований. Здесь следует отметить видного французского ассириолога Ф. Тюро-Данжена, который первым начал систематическую публикацию текстов. (Его дело затем было продолжено А. Саксом, О. Нейгебауером, Э. М. Бройнсом.) У нас в Союзе исследованием математики Двуречья занимались М. Я. Выгодский, И. Н. Веселовский, А. А. Вайман.
При изучении математических табличек оказалось, что по содержанию они делятся на два класса:
- "тексты-таблицы" (например, содержащие таблицы умножения или таблицы квадратов)
- "тексты-задачники", содержащие формулировки и решение задач.
Все эти тексты, как оказалось, относятся к двум резко ограниченным и далеко отстоящим друг от друга периодам: большая часть их является "древневавилонской", т. е. относится ко времени династии Хаммурапи (1800-1600 гг. до н. э.), другая, меньшая часть, была составлена в эпоху Селевкидов (III-I вв. до н. э.), т. е. относится уже к эпохе эллинизма. За время, разделяющее оба периода, изменились язык и форма написания знаков, что и позволило провести строгую датировку табличек, однако математическое содержание текстов осталось в основном тем же.
Но всего удивительнее оказался тот факт, что большинство "текстов-задач" являлись задачами на квадратные уравнения! Вавилоняне за две тысячи лет до н. э. умели решать квадратные уравнения и делать алгебраические преобразования! Это было поразительное открытие, заставившее отнести начало алгебры не к V в. до н. э., как думали раньше, а к XVIII в.!
Прежде чем переходить к рассмотрению вавилонских задач, скажем несколько слов о "текстах-таблицах".
Для обозначения всех чисел вавилоняне пользовались только двумя знаками: вертикальным и горизонтальным клиньями. Эти знаки вдавливались палочкой в глину, а затем дощечка из глины обжигалась. Как же удавалось обходиться только двумя знаками?
Все числа от 1 до 9 записывались с помощью соответствующего числа вертикальных клиньев (рис. 1). Число 10 записывалось с помощью горизонтального клина. Затем все числа до 59 получались комбинацией этих двух клиньев, см., например, число 23. Число 60 снова записывалось с помощью вертикального клина, так что изображенная на рис. 1 последняя запись могла означать число 60 + 23 = 83. Мы пишем "могла означать", так как запись эта могла быть прочитана многими способами: она могла означать 1 + 23×60-1 = 1 23/60 или, например, 602 + 23 = 3623 и вообще 60k + 23*60k1, где k1<k.
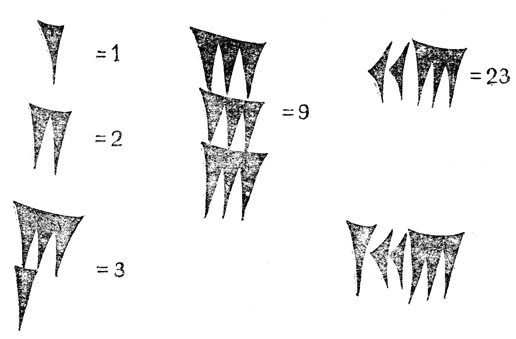
Рис. 1
Такая неоднозначность записи объяснялась тем, что у вавилонян не было нуля. Правда, в эпоху Селевкидов появился специальный разделительный знак, который ставился, если в середине числа был пропущен шестидесятеричный разряд, но в конце числа этот знак никогда не ставился.
Сделаем выводы:
- Система нумерации вавилонян была позиционной, так как числовое значение одного и того же знака определялось не только его формой, но и положением, которое он занимал в записи числа.
- Основанием системы служило число 60. Откуда взялось такое число? Обычно нумерации имеют основанием 10 - число пальцев на руках, иногда 20 (следы такой системы сохранились во французском и в скандинавских языках). Но как могло получиться 60? На этот счет существует много гипотез, ни одна из которых не является более убедительной, чем все остальные. Итак, это пока неизвестно.
- В системе не было нуля, поэтому запись не имела абсолютного характера. Какому числу на самом деле отвечала запись, приходилось определять из контекста.
Неудобства, связанные с отсутствием нуля, искупались до некоторой степени тем, что вавилоняне имели возможность сразу единообразным способом записывать и целые числа, и шестидесятеричные дроби. То есть вместе с позиционной системой у них имелись и систематические дроби.
Но при таком большом основании, как 60, довольно трудно-выучить таблицу умножения! Мы учим ее до 9×9, а вавилонским детям пришлось бы доходить до 59×59. Но, к их счастью, это им не было нужно. При раскопках нашли такое количество "таблиц умножения", что, по-видимому, их изготовляли массами для школьников и они ими пользовались при решении задач точно так же, как- мы теперь пользуемся таблицами логарифмов. Это - один из видов наиболее часто встречающихся таблиц.
Другой вид связан с операцией деления. Чтобы разделить число M на число N, вавилоняне всегда брали число ему обратное N' = 1/N и умножали М на N'. Поэтому у них большое распространение получили и "таблицы обратных величин". Количество и тех и других говорит о том, что они применялись для преподавания, что в Вавилоне должны были быть школы, в которых обучались дети. Кроме названных таблиц, имелись еще таблицы квадратов натуральных чисел, таблицы кубов, а также таблицы квадратных корней (в шестидесятеричных дробях), чисел n3 + n2 и др. Таких таблиц было меньше. Видимо, их применяли уже в специальных случаях.
Заметим, что следы вавилонской нумерации сохранились и до сих пор: мы делим час на 60 минут, а минуту - на 60 секунд, т. е. считаем время по шестидесятеричной системе. То же мы делаем при делении окружности на градусы, минуты и секунды. Такая традиция перешла к нам из астрономии. Вавилоняне первыми проводили систематические наблюдения звездного неба, составляли календарь, вычисляли периоды обращения Луны и планет, могли предсказывать солнечные и лунные затмения. Эти астрономические знания впоследствии перешли к грекам, которые вместе с астрономическими таблицами заимствовали и шестидесятеричную нумерацию. Ею пользовался и знаменитый астроном Птолемей (II в. н. э.) в своем фундаментальном труде, известном под арабизированным названием "Альмагест".
Еще позднее, в VIII IX вв., этот труд был переведен на арабский язык, а вместе с ним в обиход и арабских астрономов вошла вавилонская шестидесятеричная нумерация. Отсюда она проникла в Европу. Только в XV-XVI вв. появились десятичные дроби и начали вытеснять шестидесятеричные. Однако, как мы видели, отголоски шестидесятеричной нумерации дошли и до нас.
II. Какие же задачи решали вавилонские школьники? Существуют тексты с большим количеством однотипных задач, в которых нужно найти "длину" и "ширину" или "множимое" и его обратную величину - "множитель", для которых задана сумма или разность.
Вот одна из таких "канонических" задач:
Задача 1. "Множимое и множитель 2; 30", т. е. даны две взаимно обратные величины: "множимое" - x и "множитель" - 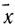 (
(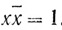 ) и x +
) и x + 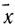 = 2; 30. Транскрипция 2; 30 означает, что мы имеем дело с числом 23060. Для облегчения чтения в дальнейшем мы будем записывать все числа в нашей десятичной позиционной системе. Таким образом, учащемуся предложена система:
= 2; 30. Транскрипция 2; 30 означает, что мы имеем дело с числом 23060. Для облегчения чтения в дальнейшем мы будем записывать все числа в нашей десятичной позиционной системе. Таким образом, учащемуся предложена система:
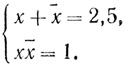
Далее в тексте описывается, какие операции нужно сделать для нахождения решения. Для того чтобы нам было легче следить за действиями вавилонского вычислителя, мы будем записывать их с помощью буквенной символики:
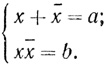
(1)
Эта система эквивалентна уравнению z2 -az + b = 0.
Итак:
- "На 0,5 умножь : 1,25" (т. е. a*0,5 = а/2).
- "1,25 на 1,25 умножь: 1,5625" (т. е. а/2*а/2 = a2/4).
- "1 вычти отсюда: 0,5625" (т. е. (а/2)2 - b).
- "Что на что надо умножить, чтобы получить 0,5625?: 0,75" (т. е. √[(а/2)2 - b].
- "0,75 к 1,25 прибавь: 2 - множимое" (т. е. x = а/2 + √[(а/2)2 - b].
- "0,75 от 1,25 вычти: 0,5 - множитель" (т. е. x = а/2 - √[(а/2)2 - b].
Мы видим, что школьнику дается рецепт или, если угодно, алгоритм для решения системы (1), равносильный хорошо известной нашей формуле. То, что мы записываем в виде формулы, вавилоняне задавали как строго определенную последовательность операций. Но как же было получено такое решение?
Прежде чем попытаться ответить на этот вопрос, рассмотрим некоторые другие задачи.
Чтобы школьник лучше усвоил способ решения, в таблицах приводится большое количество однотипных задач, причем имеющих, как правило, одни и те же ответы. Это задачи, которые мы бы записали с помощью уравнений:
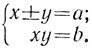
Это - канонические системы. Но затем задачи усложняются. Предлагаются задачи, которые еще нужно свести к каноническим. Вот пример одной из них:
Задача 2. "Длина, ширина. Длину и ширину я перемножил и площадь получил. Затем избыток длины над шириной я прибавил к площади: 183 получилось у меня. Затем я длину и ширину сложил: 27. Спрашивается длина, ширина и площадь".
Итак, предложена система:
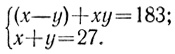
(2)
Решение: "Ты сделаешь так", и далее приводится следующая последовательность операций:
- 27 + 183 = 210.
- 27 + 2 = 29.
- 29×0,5 = 14,5.
- 14,5×14,5 = 210,25.
- 210,25 - 210 = 0,25.
- "Что на что надо умножить, чтобы получить 0,25?:0,5".
- 14,5 + 0,5 = 15 - длина.
- 14,5 - 0,5 = 14 - ширина.
- "Отними 2, которое ты прибавил к 27, от ширины 14; 12 - истинная ширина".
- "15 - длину, 12 - ширину я перемножил, 180 - площадь".
В чем же смысл этого решения? Проанализировав действия вавилонского вычислителя, можно заметить, что, начиная с пункта 3) и до пункта 8), он пользуется алгоритмом для решения системы:
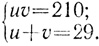
Из пункта 9) мы узнаем, что x= u = 15, а y = u - 2 = 14 - 2 = 12. Кроме того, мы знаем, что 210 - это сумма 183 и 27, а 29 - это сумма 27 и 2. Итак, вавилонский математик с самого начала сложил уравнения системы (2):
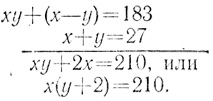
Обозначив y + 2 через v, можно получить:
xv = 210,
x + v = x + y + 2 = 27 + 2 = 29.
т. е. получить именно ту систему, которую решает вавилонский математик в пунктах 3)-8).
Наша реконструкция потребовала от нас умения складывать выражения (x - y) и (x + y), а также умения выносить в выражении xy + 2x множитель x "за скобки". Можно ли предполагать, что вавилонские математики умели проделывать такие операции?
На этот вопрос следует ответить утвердительно. Рассматриваемая ниже задача 3 показывает, что они знали даже такие формулы:
(a + b)2 = a2 + 2ab + b2.
Задача 3. Площадь двух моих квадратов я сложил: 1825, сторона второго квадрата равна 2/3 стороны первого и еще 5GAR*, т. е.
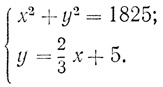
* (GAR - мера длины.)
Чтобы подставить у в первое уравнение, необходимо воспользоваться- следующей формулой:
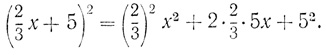
Тогда для x получаем квадратное уравнение:
ax2 + 2bx = c.
где
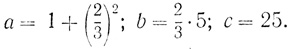
В тексте сначала вычислены коэффициенты a, b, c, а затем найдены:
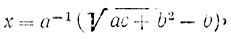
y = 2/3x + 5.
III. Нас, естественно, интересуют два весьма трудных вопроса:
- была ли у вавилонян алгебра?
- как возникли те задачи, которые мы находим в вавилонских текстах?
Чтобы ответить на первый из этих вопросов, надо уяснить, что мы понимаем под алгеброй.
Современная алгебра понимается как учение об операциях над произвольными математическими объектами (обозначаемыми буквами), причем операции эти, как правило, являются "законами композиции" (или бинарными отношениями), позволяющими двум объектам из одного множества ставить в соответствие третий объект из этого же множества. Такими "законами композиции" могут быть сложение, умножение чисел или, например, сложение векторов.
Если, например, заданы некоторое множество M объектов {α, β, γ, δ ...} и для них некоторый закон композиции ⊗, обладающий свойствами:
- если α∈M и β∈M, то α⊗β ∈M,
- α⊗(β⊗γ) = (α⊗β)⊗γ (ассоциативность),
- существует элемент e, такой, что для любого α ∈M α⊗e = e⊗α = α
- для всякого α ∈M существует такое α' ∈M, что α⊗α' = α'⊗α = e,
то множество M называется группой (группа - одна из алгебраических структур).
Итак, вопрос о наличии алгебры в Древнем Вавилоне сводится к двум основным вопросам:
- была ли у вавилонян буквенная символика?
- знали ли они законы арифметических операций (законы композиции)?
Мы настолько привыкли к буквенному исчислению, что нам без него сейчас трудно даже представить математику. А между тем буквенное исчисление было создано лишь в конце XVI в. До этого, по крайней мере на протяжении 34 веков, математика существовала и развивалась без такого исчисления, т. е. без формул!
Разберем характерные черты буквенных обозначений, посмотрим, чего мы достигаем, вводя символы. В чем, например, принципиальная разница в записи:
(a + b)2 = a2 + b2 + 2ab
и в фразе. "Квадрат суммы двух количеств равен квадрату первого количества, плюс квадрат второго количества, плюс удвоенное произведение первого на второе"?
Конечно, первая запись короче. Но дело не только и не столько в этом. Дело в том, что над словами не определены никакие математические операции, мы не можем их складывать или умножать друг на друга. С символами же мы можем оперировать - и это главное. Например, подставляя вместо b сумму p + q, мы получаем:
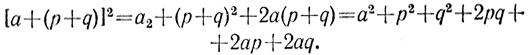
Причем новая формула получена чисто механически, без привлечения логических рассуждений, а только с помощью правил исчисления. Лейбниц писал, что буквенное Исчисление "разгружает воображение".
Теперь мы можем сказать, что буквенной символики у вавилонян не было. У них имелись специальные термины для слов "длина", "ширина", "множимое" и "множитель", причем это были шумерские слова, которые ярко выделялись среди прочего текста. (Шумеры были древними обитателями Двуречья. Около XXIII в. до н. э. они были завоеваны и, по-видимому, ассимилированы семитическим племенем - аккадянами.) Эти слова как будто играют роль символов, но с ними никогда не оперируют (нет даже правил их переноса из одной части уравнения в другую).
Перейдем теперь к вопросу об общих законах арифметики у вавилонян.
Прежде всего, как могли вавилоняне найти алгоритм решения системы:
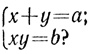
Вероятно, они рассуждали так: если бы x = y = 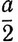 то xy =
то xy = 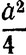 Если b≠
Если b≠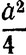 . то пусть x превосходит
. то пусть x превосходит 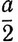 на некоторую величину, а y - меньше
на некоторую величину, а y - меньше 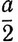 на ту же величину:
на ту же величину:
x = 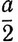 + z,
+ z,
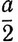 + z,
+ z,y = 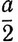 - z.
- z.
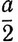 - z.
- z.
Тогда 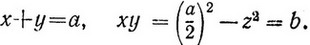
Откуда находим: 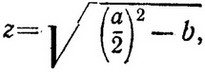 а затем x и y. Если вавилоняне рассуждали именно так, то они должны были знать, что (a + b)(a - b) = a2 - b2. И они действительно знали эту формулу! Задача 2, которую мы привели, показывает их умение выносить общий множитель за скобки и делать подстановку, а задача 3, что им была известна формула (a + b)2. Другие задачи, о которых мы, правда, не говорили, показывают, что вавилоняне знали и формулу для (a - b)2. Итак, вавилонские математики знали общие законы операций сложения и умножения и пользовались ими.
а затем x и y. Если вавилоняне рассуждали именно так, то они должны были знать, что (a + b)(a - b) = a2 - b2. И они действительно знали эту формулу! Задача 2, которую мы привели, показывает их умение выносить общий множитель за скобки и делать подстановку, а задача 3, что им была известна формула (a + b)2. Другие задачи, о которых мы, правда, не говорили, показывают, что вавилоняне знали и формулу для (a - b)2. Итак, вавилонские математики знали общие законы операций сложения и умножения и пользовались ими.
Далее, они применяли эти законы для получения формулы решения квадратного уравнения, и наконец, для преобразования более сложных уравнений к каноническим.
Все это приводит нас к выводу, что в вавилонской математике XIX-XVIII вв. до н. э., несмотря на отсутствие символики, появились элементы алгебры.
Как же все-таки возникли задачи на квадратные уравнения? При измерении полей, естественно, возникает такая задача: измерены длина и ширина поля, найти его площадь. Но никогда не возникнет задача: известны площадь и периметр участка, найти его стороны.
Мы полагаем, что задачи последнего типа появились в результате научного анализа применяемых методов. Пусть мы знаем длину x и ширину y, тогда мы можем вычислить полупериметр x + y и площадь xy. Как проверить, правилен ли наш результат? Можно ли сделать "проверку", т. е. по данным xy и x + y найти x, y? Возможно, таким образом могла возникнуть первая "обратная задача", которыми так богато последующее развитие математики.
Разберем этот вопрос подробнее. В своей книге по истории математики в средние века А. П. Юшкевич охарактеризовал задачи на "обращение" следующим образом: "В плане более отвлеченного развития происходило обращение ряда задач - практически данные величины принимались за искомые, а искомые - за данные; это явилось одной из предпосылок разработки алгебраических приемов"*.
* (А. П. Юшкевич. История математики в средние века, М., 1961, с. 11.)
Приведем несколько примеров:
Прямая задача 1. Дана сторона квадрата a. Найти площадь y = a2. Для ее решения надо заданное число a умножить само на себя.
Обратная к задаче 1. Дана площадь квадрата b. Найти его сторону.
Теперь y = b - заданная величина, а сторона квадрата x - искомая: x2 = b.
Для решения задачи надо_из заданного числа b извлечь квадратный корень: x = √b.
Прямая задача 2. Даны стороны прямоугольника a и b. Найти его площадь S.
Задача решается при помощи умножения:
S = ab.
Как поставить обратную задачу? Если просто задать площадь S и потребовать определения сторон x и y, то задача будет неопределенной. Доопределить ее можно двумя способами:
1-я обратная к задаче 2. Дана площадь прямоугольника S и одна из сторон y = a. Найти другую сторону, т. е. ax = S.
И решение задачи сводится к делению: x = S/a.
2-я обратная к задаче 2. Дана площадь прямоугольника S и сумма (или разность) двух его сторон, т. е.
xy = S; x ± y = b.
В этом случае задача сводится к эквивалентному квадратному уравнению:
z2 ± bz ± S = 0.
Последняя задача является принципиально более сложной, чем первоначальная прямая или 1-я обратная к ней. Ее анализ и привел вавилонских математиков почти за 4 тыс. лет до наших дней к открытию формулы решения квадратных уравнений. При этом, как мы видели, использовались алгебраические преобразования.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'