Дело Адамса-Эри

Обзор^*. Адаме посетил Королевскую обсерваторию 21 октября 1845 г., не смог увидеть Эри и оставил записку с кратким извещением о своем предсказании относительно N. Ответное письмо Эри (от 5 ноября) содержало вопрос о том, "объясняются ли отклонения радиуса-вектора той же теорией, которая объясняет отклонения в долготе". Адам не ответил. Фактические наблюдения не начинались до 29 июля 1846 г., когда Чаллис приступил к выполнению полной (к сожалению, слишком полной) программы поисков, продолжавшихся до конца сентября. Леверрье послал свое предсказание в Берлинскую обсерваторию, где Галле нашел N (при помощи незадолго до того опубликованной карты неба) 23 сентября, в тот же самый день, когда пришло письмо Леверрье.

^* (Полный отчет занимает - большую часть статьи Смарта: с. 19-43 (см, с. 120).)

То, что я имею сказать, относится как раз к r-поправкам. Адаме приступил к работе в полной уверенности, что причиной плохого поведения V является неизвестная планета, и с ясным представлением о том, как математически подойти к задаче; он был полностью поглощен своей работой и все время находился, если так можно выразиться, "при исполнении служебных обязанностей". Эри не занимался этим вопросом и думал, что в этом темном деле существует много других возможностей объяснения ненормальностей в поведении U, к идее новой планеты он относился скептически, что в 1845 г. было вполне объяснимо. (Опираясь на прошлый опыт, он, вероятно, считал, что методы теории возмущений требуют экспериментальных данных, относящихся к нескольким оборотам, т. е. результатов наблюдений многих сотен лет.) Однако он поставил вопрос о r-поправках, и этот вопрос, к сожалению, стал его идеей-фикс. (В своем объяснении перед общим собранием Королевского общества 13 ноября 1846 г. Эри говорил: "Я поэтому считал вопрос, может ли теория, объясняющая отклонения в долготе, объяснить и отклонения в радиусе, настоящим experimentum cruets. И я с большим нетерпением ожидал ответа мистера Адамса на этот вопрос. Если бы ответ был положительный, я бы сразу употребил все свое влияние" и т. д.) Адаме (который с самого начала и до конца был по отношению к Эри весьма вежлив и почтителен) фактически на этот вопрос так и не ответил. Его личное мнение^* состояло в том, что вопрос тривиален. Вот что он писал Эри 18 ноября в ответ на цитированное выше выступление (я опускаю его вежливые извинения): "В течение нескольких прошедших лет наблюдаемое положение Урана все больше и больше отставало от его табулированного положения. Другими словами, фактическое угловое движение Урана было значительно более медленным, чем то, которое предсказывалось таблицами. Мне кажется, что это ясно показывает, что таб-| личный радиус-вектор любой теорией, правильно представляющей движение Урана по долготе, будет значительно увеличен, так как изменение правой части равенства

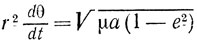
очень мало^**. В соответствии с этим я нашел, что если просто исправить эллиптические элементы так, чтобы удовлетворить как можно точнее современным наблюдениям без учета других дополнительных возмущений, то соответствующее увеличение радиуса-вектора не будет очень отличаться от того, что дает моя теория". (Остальное несущественно для наших целей.)

^* (Сообщенное им в разговоре с Глейшером в 1883 г.)

^** ([r^2dθ/_dt - угловой момент (кратко: у. м.).- Дж. И. Л.])

Я нахожу, что эта цитата (как и многое из того, что писалось 80 лет назад^*) не является образцом кристально ясного изложения; но самый важный пункт, касающийся того, что, по мнению Адамса, у. м. изменяется очень мало, не мог бы быть изложен яснее. "Постоянство" у. м. устанавливало бы очень простую связь между θ-отклонениями и r-отклонениями. Чаллис (после открытия N) соглашается с мнением Адамса: "Совершенно невозможно исправить долготу (U) по наблюдениям в течение, по крайней мере, 180 лет независимо от исправлений радиуса-вектора..." Мнение Адамса окончательно подтверждается вычислениями: изменение у. м. очень слабо влияет на θ-эффекты.

^* (Тогда надо было быть по крайней мере доцентом, чтобы с пониманием читать научную статью; сегодня любой аспирант может читать все.)

Первое, что надо отметить,- это то, что Адаме и Эри частично говорили о разных вещах. Точка зрения Эри: я сомневаюсь, чтобы объяснение заключалось в наличии неизвестной планеты, но я готов рассмотреть эту возможность, если она объясняет отклонения r так же хорошо, как отклонения θ. Точка зрения Адамса: вопрос решается новой планетой, и если ее определить так, чтобы совпадали θ, то автоматически (ввиду имеющихся ("связей") совпадут и значения r. Вина Адамса заключалась в том, что он не хотел понять точку зрения Эри; впоследствии он сам признал, что на вопрос Эри он должен был сразу дать обоснованный ответ. По-видимому, сыграло роль и то обстоятельство, что, будучи очень тонким математиком, Адаме был в то же время типичным кембриджским "первым призером" (молодой самоуверенный талант; все знания и идеи разложены по полочкам и в любой момент под руками; соображает быстро и без усилий). Пожилые люди, стремящиеся не утруждать себя размышлениями, если обстоятельства это позволяют, могут показаться ему медлительными и глупыми^*. Следует всегда отвечать на тривиальные вопросы ваших старших коллег (тем более, что и молодой талант все же может чего-нибудь не учитывать).

^* (Люди, не встречающиеся со знаменитостями в часы их досуга, вряд ли представляют себе, какие глупости эти знаменитые' люди в состоянии высказывать. Я вспоминаю две беседы за профессорским столом в кембриджском Тринити-колледже. Одного из самых известных биологов спросили, будут ли сыновья двух отцов-близнецов, женатых на двух сестрах-близнецах, похожи друг на друга; он ответил: "конечно", и был тут же поправлен одним быстро реагирующим философом. В другой беседе участвовали Резерфорд, Фаулер, по крайней мере еще один физик и я; мы безнадежно запутались в вопросе о связи между экспериментом с падением монеты и перышка в пустоте и фактом независимости вязкости от плотности. Не является ли этот эксперимент вообще блефом? Резерфорд извиняющимся тоном сказал, что, кажется, он сам видел этот опыт в юности. Мы продолжали обсуждение после ужина, когда нас вывел из тупика один инженер.)

До сих пор я скрывал от читателя тот факт, что в решающем теоретическом вопросе об у. м. Адаме был абсолютно неправ. Относительное изменение у. м. того же порядка, что и θ - ошибка. Это очевидно даже с позиций школьной математики (возьмем "моменты" относительно S:N сильно влияет на у. м.)^*. Точка зрения Адамса последовательно основывалась на теории возмущений, но и с этих позиций, если даже и за "первым призером" признать право ошибаться, ошибка Адамса выглядит по крайней мере странной^**. Численное подтверждение точки зрения Адамса представляет собой последний штрих этой комедии. В словах "мало изменяется" слово "мало" понимается в том смысле, что 15% - это малое изменение, но не "очень" малое (выражение Адамса). Так или иначе, эта малость является случайным следствием числовых постоянных; например, при "далеком" N ее уже нет.

^* (Полный анализ круговой орбиты, конечно, подтверждает это.)

^** (1-е² "мало изменяется", но что заставило его думать, что а ведет себя так же?)

Постскриптум о небесной механике. Я закончу эти замечания раскрытием секрета одной моей собственной работы, из которой вытекает, что в гравитирующей системе тел (обобщение солнечной системы) никогда не может произойти захвата (или, наоборот, потери) даже пылинки^*. Этот результат имеет характер сенсации (я не встретил ни одного математика, который не был бы удивлен, услышав о нем), так как он противоречит общему мнению. Добавлю, что, во-первых, это не означает немедленного ухода пылинки, она может удерживаться в системе любое число биллионов лет. Существуют даже предельные случаи, в которых захват перманентен; но эти случаи должны быть отброшены как бесконечно редкие, так же как мы отбрасываем перманентные состояния неустойчивого равновесия (булавка на острие). Эти бесконечно редкие случаи, однако, показывают, что теорема не может быть тривиальной. Во-вторых, доказательство никоим образом не утверждает, что уходит именно пылинка: уйти может и Юпитер.

^* (Тела рассматриваются как точечные массы (чтобы избежать трудностей, связанных с соударением тел конечных размеров), подчиненные закону обратных квадратов ньютонова тяготения (последнее, вероятно, несущественно). Мне не удалось обнаружить более ранней формулировки этого результата.)

Эта теорема является следствием следующей теоремы: допустим, что система была заключена в фиксированной сфере S для всех отрицательных времен, тогда (за исключением бесконечно редких случаев) она будет находиться в этой сфере и для всех положительных времен. Аналогичное утверждение имеет место и при перестановке положительных и отрицательных времен. (Чтобы убедиться в том, что предыдущая теорема действительно является следствием этой теоремы, заметим, что любой настоящий захват (соответственно, настоящая потеря) означает отличие прошлого от будущего, что исключается.)

Возьмем последнюю теорему в ее формулировке с переставленными будущим и прошлым (эта формулировка несколько более удобна); идея доказательства заключается в следующем. "Система" ассоциируется с ее точкой-представителем (кратко m. -n.) Р "фазового" пространства, которая задает начальные условия в фиксированный момент времени t₀, например t₀ = 0^*. Теперь рассмотрим множество V (в 6n-пространстве) всех точек Р, представляющих системы, которые (в астрономическом пространстве) остаются в сфере S для всех положительных времен. "Система" Р имеет новую m.-n. Р' (координаты х, ..., х, ...), соответствующую, скажем, моменту t = 1 множеству V точек Р, таким образом, будет соответствовать множество V точек Р'. Существует известная теорема, которую мы примем без доказательства, утверждающая, что (6n-мерные) объемы V и V равны между собой [так как дифференциальные уравнения системы "консервативны"]^**.

^* (Если система состоит из n + 1 тела, то фазовое пространство имеет 6я "измерений", а именно: n (астрономических) пространственных координат x₀, y₀, z₀ и n соответствующих скоростей х^.₀, y^.₀, z^.₀, n из этих тел в момент t₀. )

^** (Любое множество V имеет один и тот же объем во все моменты t. Для математика-профессионала доказательство умещается в одной строке (если можно якобиан назвать строкой).)

Далее, множество V может рассматриваться в том же 6n-пространстве, что и множество V. Для того чтобы m.-n. Р принадлежала к V, она должна выдержать некоторое вступительное испытание, заключающееся в том, что все тела должны оставаться в S во все последующие моменты времени. Но если Р' из V получается из Р, входящего в V, то "будущее" Р' начинается на единицу времени позже, чем "будущее" Р, и, следовательно, Р' выдерживает вступительное испытание. Итак, множество V содержится в множестве V. Но их объемы равны. Все это вместе взятое означает, что V' и V тождественны [как множества: набор Р' совпадает с набором Р]. Поэтому любая точка Q из V является некоторой точкой R из V'.

Будем теперь исходить из некоторой точки Q из V и рассмотрим соответствующую m.-n. в момент t = -1 (момент прошлого, на единицу времени более ранний). Q является каким-то R из V и, следовательно, получается (в том же смысле, в каком Р' получается из Р) из некоторого Т из V. Эта точка Т является m.-n. P при t = -1. Мы приходим к заключению, что при t = -1 m.-n. любого Р из V сама лежит в V. Это заключение можно неограниченно продолжать в прошлое: если Р находится в У в момент t = 0, то соответствующая m.-n. принадлежит к V во все моменты (t = -m) сколь угодно далекого прошлого. Это означает, что все тела системы оставались в S в течение всего прошедшего времени, и доказательство закончено.

Приведенное рассуждение является поразительным примером силы общих соображений. Если бы основные идеи этого рассуждения принадлежали мне, то я действительно имел бы чем гордиться; но они известны уже по крайней мере в течение 60 лет. Со мной же произошло следующее. Читая курс дифференциальных уравнений, я встретился с уравнениями, для которых объем множеств V убывает с возрастанием t. Мне пришла в голову "теорема о постоянном объеме" (кстати, я впервые узнал о ней незадолго до этого) и, чтобы немного отвлечься, я переключился на небесную механику. После лекции я пошел на прогулку, и изложенное выше доказательство промелькнуло у меня в голове (буквально в течение нескольких секунд). Моей первой реакцией было отвергнуть мысль о публикации столь мало оригинальной вещи. Но так как я имел обязательство написать статью для одной Festschrift, а у меня в тот момент ничего другого не было, то я решил внимательно продумать все детали доказательства.

Так обычно поступают все, кому иногда приходит в голову что-либо новое. Оказалось, что, строго говоря, мое рассуждение содержит некоторые ошибки (фактически оно содержит 3 неверных заключения). Любой компетентный аналитик может избавиться от них, и в результате возникает довольно содержательная работа. Так появилась на свет моя "находка"^*: блестящие идеи, не мои, плюс математическая рутина.

^* (Статья напечатана в Communication du seminaire mathemati-que de l'Universite de Lund, tome supplemental (1952), dedie a Marcel Riesz. Она содержит добавление, в котором показывается, что предположение о равенстве масс нулю может быть отброшено. Это небольшое замечание вовсе не тривиально; в действительности мне пришлось потрудиться над ним две недели. (Хотя основная идея этого добавления требует для своей формулировки нескольких страниц, она тоже пришла мне в голову во время прогулки, на этот раз буквально в течение доли секунды.))