Лев и человек

"Лев и человек, находящиеся на огороженной круглой арене, имеют одинаковую максимальную скорость. Какой стратегии должен придерживаться лев, чтобы быть уверенным в своей трапезе?"^*.

^* ("Кривая погони" (L бежит всегда прямо на М) требует бесконечного времени, так что формулировка задачи не лишена смысла.)

Говорят, что задача о "взвешивании монет" стоила 10 000 человеко-часов непродуктивно потраченного времени математиков, занятых оборонной работой во время войны. Было даже сделано предложение сбросить эту задачу над Германией. Задача о льве^*, хотя и имеет уже 25-летнюю давность, недавно вновь пронеслась по стране; но большинство из нас удовлетворилось ответом "L (лев) все время должен находиться на радиусе ОМ (М - человек)".

^* (Придумана Р. Радо (но не опубликована).)

Если L сходит с ОМ, то асимметрия идет на пользу М. Поэтому L придерживается ОМ и всякая иррегулярность в поведении М помогает L. Примем поэтому для простоты, что М бежит по окружности С радиуса а с угловой скоростью ω. Тогда L (придерживаясь радиусов) бежит по окружности, касающейся С^*, скажем, в точке Р и М оказывается пойманным за время, меньшее 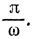. Это легко следует из уравнений движения L, а именно 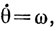r^.2 + r²cos² = a²ω². Поучительно, однако, подробнее исследовать движение вблизи Р. Здесь мы имеем

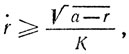
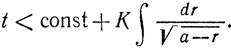
^* (Случай, когда движение L начинается в О, особенно ясен из геометрических соображений.)

Интеграл сходится (при r→a) с большим запасом - настолько большим, что принятое нами упрощающее условие представляется полностью оправданным. *Математик-профессионал легко проверит, что когда М движется по развертывающейся спирали, приближаясь к окружности, то, применяя легко понятное обозначение x = r_M - r_L (теперь ω - уже переменное), мы будем иметь

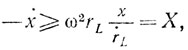
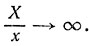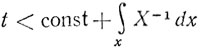где Тогда и этот интеграл возрастает медленнее, чем 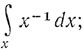поэтому можно, вообще говоря, с уверенностью предположить, что интеграл сходится.*

Несмотря на все это, "ответ" неверен: М может избежать поимки (как бы L себя ни вел). Это было совсем недавно обнаружено профессором А. С. Безиковичем; далее следует первое (и единственное) опубликованное доказательство.

Я начну с того случая, когда L придерживается ОМ; в этом случае все рассуждения легко проводятся (и во всяком случае этого достаточно для доказательства неверности "ответа"). Исходя из начальной точки М₀ при t = 0, проведем ломаную М₀М₁М₂... со следующими свойствами: (I) М_nМ_n+1 перпендикулярно к ОМ_n, (II) длина ломаной бесконечна, (III) ломаная остается внутри круга с центром в О, не выходящего за пределы арены. В самом деле, если положить l_n = M_n-1M_n, то мы имеем OM²_n = OM²₀ + 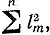и все будет обеспечено при 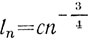с соответствующим образом подобранной постоянной с. Пусть М бежит вдоль этой ломаной (a L, как условлено, придерживается ОМ). Так как М₀М₁ перпендикулярно к L₀M₀, то L не может поймать М, пока М находится на M₀M₁. Так как, далее, L₁ находится на ОМ, а М₁М₂ перпендикулярно к L₁M₁, то L не может поймать М, пока М находится на М₁М₂. Это продолжается на каждом последующем звене M_nM_n+1 и, следовательно, в течение бесконечного времени, так как общая длина ломаной бесконечна.

*Я добавлю набросок поразительно короткого доказательства в общем случае. Пусть дано М₀ и L₀;M выбирает подходящее О и "строит" описанную выше ломаную М₀М₁М₂ ..., но бежит вдоль другой ломаной М₀М'₁М'₂..., ассоциированной с первой и зависящей от того, что делает L. M₀M₁ проводится перпендикулярно к L₀M₀; если N₀ - основание перпендикуляра, опущенного из О на М₀М'₁, то М'₁ берется на продолжении M₀N₀ так, чтобы было N₀M'₁ = l₁(= M₀M₁). Если L находится в L₁, когда М прибывает в М'₁, то M'₁M'₂ проводится перпендикулярно к L₁M'₁ и М'₂ выбирается на этой прямой так, чтобы было N₁M'₂ = l₂ и т. д. Ясно, что ОМ'²_n = ОМ'²_n-1 ≤ l²_n, OM'²_n ≤ OM²_n, и новая ломаная лежит внутри того же круга, что и старая. Так как M'_n-1M'_n≥l_n, то новая ломаная также имеет бесконечную длину, и L по-прежнему не сможет поймать М.*