Большие числа

(Впервые опубликовано в Mathematical Gazette.- July 1948.- V, 32, N 300. Добавления заключены в квадратные скобки.)

1. Задача представления очень больших чисел рассматривается в Исчислении песчинок Архимеда. "Неисчислимость" песчинок давно вошла в поговорку, но Архимед разработал схему - эквивалент обозначения 10ⁿ, согласно которой "Вселенная" - сфера, доходящая до Солнца, с диаметром, не превышающим 10¹⁰ стадий,- будучи наполнена песком, содержит менее чем "1000 единиц седьмого разряда чисел", т. е. менее чем 10⁵¹ песчинок. [За основание того, что мы сейчас назвали бы степенью, Архимед берет 108 ("мириад мириадов") и рассматривает "периоды", содержащие каждый 10⁸ "порядков" чисел; последним числом схемы является 10⁸*10¹⁵.] Задача представления упирается в изобретение подходящих обозначений; Архимед не располагал нашими обозначениями а^b с его возможным обобщением a^aa.... Мы вернемся к этому вопросу в конце; он далеко еще не исчерпан.

2. Древние индийские рукописи много раз с благоговением обращаются к идее представления колоссальных отрезков времени. (Мне кажется, что следующий пример я взял из книги Бокля История цивилизации в Англии; несомненно, что сам я не мог этого выдумать.)

Имеется камень размером в кубическую милю, в миллион раз тверже алмаза. Один раз в миллион лет святой муж подходит к этому камню и слегка дотрагивается до него. В конце концов, в результате этих легчайших прикосновений камень износится. Вычисления показывают, что это произойдет через 10³⁵ лет: жалкий результат, учитывая столь богатую фантазию! Кстати, это - пример "недостаточности" популярных представлений о колоссальном.

3. Когда древние греки стали рассматривать небесные тела как разбросанные в "обычном" пространстве, был совершен большой скачок в развитии наших представлений о Вселенной. Аналогичный, хотя и меньший, скачок был необходим для введения широко известных теперь рассуждений, связанных с эрозией и т. п. Легко представить себе Архимеда в качестве автора таких рассуждений, но, насколько мне известно, Греция не является их родиной. Интересно подсчитать, например, непостижимое для человеческого разума время, необходимое для образования долины в результате размывающего действия ручейка; одна двадцатая дюйма в год дает милю в 10⁶ лет; продолжая, мы получим тысячу миль в 10⁹ лет. (Эти периоды являются естественными единицами счета времени: второй из них сравним с возрастом Земли, первый - с временем, необходимым для превращения обезьяны в доктора наук.) Ньютон оценил расстояние до Сириуса (в астрономических единицах), предполагая, что Сириус сравним по своим размерам с Солнцем. Его метод заключался в сравнении Сириуса с Сатурном, альбедо которого он довольно точно установил.

4. Следующими двумя примерами я заканчиваю свои ссылки на прошлое. Первым из них является точность угловых измерений Тихо Браге. Ошибка этих измерений не превышала 1' (у Гиппарха - 4'). Вторым - Самосский туннель, который строился во времена Пифагора и имел 900 ярдов в длину. Его прокладка началась с противоположных концов, и современные раскопки показали, что строители разошлись в середине лишь на несколько футов. Проще всего не верить, что это объясняется высокой точностью геодезических измерений и расчетов. Хотя основные свойства подобных треугольников были известны еще со времен Фалеса, я не могу допустить мысли о такой точности измерительных приборов в те времена. С другой стороны, я могу легко поверить в точность проведения наземных направлений при помощи провешивания или при помощи наблюдений какой-либо звезды из двух точек.

5. Я перехожу к современности, но продолжаю говорить об измерениях.

Мы все знаем, что измеряемые параллаксы имеют порядок 0,001"; представляет ли себе читатель, что это - угол, под которым видна монета достоинством в пенс с расстояния в 4000 миль?

Среди результатов измерений, используемых в научных вычислениях, самыми точными являются измерения времени в астрономии, в которых число значащих цифр доходит до 15: измеряются промежутки времени от 0,001" до 10² или 10³ лет, и для вычислительных целей сохраняются еще 2-3 цифры.

Однажды я спросил Эддингтона, с какой точностью возможны измерения угловых расстояний между двумя звездами, для которых оно велико. Ответ (последовавший мгновенно) гласил: "0,1"", что меня очень поразило, так как чисто механические трудности таких измерений, так же как и трудности, связанные с рефракцией, представляются непосвященному огромными.

Расскажу еще об одном удивительном факте. Официальные инструкции по производству геодезических работ предписывают для линейных измерений использование мерной ленты длиной в 130 дюймов; это не вызывает удивления. Но для угловых измерений должна использоваться "база" длиной в 9 миль - это примерно в 100 раз больше, чем я ожидал. В таких делах, впрочем, настоящие трудности возникают обычно там, где их меньше всего ждут, и оказываются часто мало интересными. В геодезических измерениях главная трудность заключается, по-видимому, в том, чтобы установить теодолит в точности над нужной точкой.

6. Перейдем теперь к рассмотрению кратных показателей и их основных свойств как "аппроксимирующих" чисел. Так как "порядок" имеет в математике и в приближенных вычислениях вполне определенный, но не подходящий для нас смысл, то будем говорить о типах чисел; именно, числа

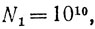
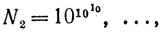
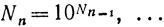
будем называть принадлежащими к типу 1, 2, ..., n, ... Далее мы будем говорить, что, например, число

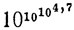
принадлежит к типу 2,47, и будем записывать его в виде N_2,47. Эта запись указывает на то, что тип этого числа лежит между 2 и 3; принятые обозначения содержат, правда, некоторую неточность, состоящую в том, что N₂ - это не N_2,0, a N_2,1, но с этим можно примириться. Вместо N_2,47 мы будем также писать N₂(4,7); отметим, что N_n = N_n(1). Число 10⁷⁹ всех элементарных частиц во Вселенной, которое мы (принося извинения за то, что выбрана малая буква) обозначим через u, есть N_1,79.

Принцип, который я хочу сейчас установить, может быть проиллюстрирован следующими примерами. Число типа, большего или равного 2, остается "практически неизменным" при возведении в квадрат; число типа, большего или равного 3, остается "неизменным" даже при возведении в степень u. Действительно,

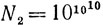
и

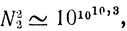
далее,

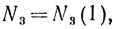
а

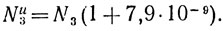
С другой стороны, N₂ почти не изменяется, если в его нижнем основании 10 заменить на u, и остается "неизменным", если 10 заменить на 2. Другим важным фактом является "равенство" таких чисел, как N!, N^N и 2^N, если тип N не меньше 1.

Эти рассмотрения мы можем теперь обобщить в следующем "принципе грубости": при оценке числа

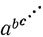
важно не допускать больших ошибок в самом верхнем показателе, но можно применять весьма грубые оценки в отношении основания и нижних показателей.

7. Перехожу теперь к числам, непосредственно связанным с повседневной жизнью (что я имею в виду под "косвенной" связью, будет ясно из § 11). Диапазон от едва слышимого звука до звука, почти невыносимого по своей громкости (одинаковой частоты, близкой к области наибольшей чувствительности уха), превосходит 10¹². Для света он даже больше, чем для звука (этого, конечно, и следовало ожидать). Поверхность Солнца имеет яркость в 6*10⁵ большую, чем поверхность Луны при полнолунии (между прочим, Солнце в 5*10⁶ ярче, чем половина Луны). Песчаная поверхность, освещенная полной Луной, по яркости находится в таком же отношении к лунному диску, как этот последний к Солнцу. Каждый, кому приходилось ходить по проселочной дороге в безлунную облачную ночь, знает, что дорога и предметы на ней все же различимы (мне неизвестно ни одно удовлетворительное объяснение того, откуда берется в этом случае свет); тут мы имеем дело еще с одним множителем, не меньшим, чем 10³ (а я бы сказал, 10⁴ или еще большим), так что в итоге отношение получается равным 10¹⁴ или 10¹⁵.

Не так давно можно было купить 1013 эргов за 4 пенса; здесь ничего не имеется в виду относительно энергии и массы - просто такова была плата за отопление в Англии. Но, конечно, эрг обсурдно мал, а механический эквивалент тепла очень велик.

8.Совпадения и маловероятные события. Каждый год поступает сообщение, что у кого-то при игре в бридж было на руках 13 карт одной масти. Вероятность такого распределения карт при сдаче равна 2,4*10^-9; если предположить, что 2*10⁶ людей в Англии играют каждый по 30 партий (участвуют в 30 сдачах) в неделю, то мы получим вероятность такого же порядка. Прежде я думал, что тасовка карт при игре в бридж недостаточна для того, чтобы считать карты на руках полностью случайными; книга Бореля о бридже убедила меня, однако, в том, что, поскольку порядок карт на руках у данного игрока безразличен, обычный процесс перетасовывания обеспечивает случайность карт. (Однако для пасьянсов это не так: в этом случае для уничтожения всякого порядка карты надо тасовать гораздо дольше; я убедился в этом на практике в период увлечения пасьянсами, и мои наблюдения были подтверждены другими.)

Мне случалось задавать вопрос: какое самое удивительное совпадение встретилось вам в жизни, и является ли оно действительно столь удивительным? (Имея в виду, что выбирать можно из всей жизни, 1:10⁶ надо считать пустяком.) Хотя эта тема достаточно скучная, я приведу два встретившихся мне примера, один удивительный на первый взгляд, но проигрывающий в интересе при дальнейшем рассмотрении, а другой действительно редкий. Начну со второго. Девушка шла по Уолтон-стрит (Лондон) к своей сестре Флоренс Роз Далтон, которая работала поварихой в доме № 42 по этой улице. Она прошла мимо дома № 40 и подошла к дому № 42, где поварихой работала некая Флоренс Роз Далтон, находившаяся в то время в двухнедельном отпуске; эту Флоренс Роз Далтон в качестве поварихи заменяла ее сестра. Но этот дом оказался домом № 42 по Овингтон-сквер (откуда в этом месте есть узкий проход на Уолтон-стрит), дом же № 42 по Уолтон-стрит был следующим (я в то время жил в доме № 42 по Овингтон-сквер и узнал об этом случае в тот же вечер). Первый пример: начиная прогулку вблизи порта Уэймс, мы видели на рейде 7 судов, которые, когда мы, пройдя 3 мили, присели отдохнуть, превратились в 6; эти 6 судов стояли параллельно, а обе мачты седьмого точно заслонялись одной мачтой одного из 6. На расстоянии 5 ярдов в ту или иную сторону от места, где мы остановились, мачты всех семи судов уже были, ясно различимы. Вероятность остановиться в пределах 10 ярдов равна 1:600, вероятность нахождения трех мачт в одной плоскости равна 1:60; в итоге это дает примерно 1:4*10⁴. Этот пример показывает, что события, почти невероятные на первый взгляд, могут фактически иметь не столь уж малую вероятность.

Безусловно, некоторое количество удивительных совпадений должно было иметь место в действительности, и я сожалею, что знаю очень мало примеров таких совпадений. В книге Дороти Сейерс Непопулярные мнения рассказывается про двух негров, носивших одно и то же имя Уилл Уэст, которые были в один и тот же день заключены в Ливенуорсскую тюрьму в США (в 1903 г.), причем данные их антропометрических измерений в точности совпадали. (Можно ли этому поверить?)

Эддингтон рассказал мне как-то про полученную обсерваторией информацию относительно новой кометы (вновь наблюденной, но не обязательно неизвестной), причем данные в телеграмме были искажены; когда же телескоп был наведен на указанное место (и был обследован, надо полагать, район с диаметром около Г), была обнаружена новая комета. (Это конечно, очень занимательный случай, но мы имеем здесь дело с вероятностью, не меньшей 1:10⁶)

9. Мы все в школьные годы забавлялись, проводя на страницах книги извилистую линию, проходящую между словами. Допустим, что мы взяли страницу энциклопедии, набранную убористым штрифтом, содержащую 100 строк, и наугад черкнули по ней линию. Принимая 1:5 за вероятность того, что эта линия пройдет между словами одной строки, мы найдем, что вероятность успешного прохождения линии через всю страницу оказывается равной 1:10⁷⁰.

Мой следующий пример, быть может, слишком далек от нашей темы. Существует способ, при помощи которого фокусник может делать вещи, на первый взгляд невозможные. Пусть выбрана какая-нибудь карта, скажем туз пик; фокусник кладет колоду карт на стол и просит кого-либо из присутствующих назвать любое число, меньшее 100; имеется немалая вероятность того, что будет названо число 37, и если оно будет названо, то фокусник предлагает отсчитать 37-ю карту колоды, которая и окажется тузом пик; если будет названо другое число, то фокусник делает какой-нибудь другой трюк. (Этот фокус может быть упрощен, если ограничиться только первыми 9 числами; очень вероятно, что названным числом будет 7 или 3; из колоды в 9 карт туз пик будет 7-й картой с одной стороны и 3-й с другой.)

К этой же категории вопросов относится нахождение вероятности того, что обезьяны, барабанящие по пишущей машинке, отпечатают Гамлета. Считая, что текст состоит из 27 000 букв и пропусков и что имеется 35 клавиш, найдем, что эта вероятность равна 1:33²⁷⁰⁰⁰ (знаменатель меньше N_1,6).

10.Игры. Допустим, что в некоторой позиционной игре существует р возможных позиций Р₁, P₂,..., Р_p. Партия представляет собой конечную последовательность позиций Р, каждая из которых получается из предыдущей в результате "хода", сделанного в соответствии с определенной совокупностью правил. Число р обычно принадлежит к типу, немного большему 1, так что число партий сравнимо с р! или с 2^р, что впервые приводит нас к числу, принадлежащему к типу, большему 2. Мы можем поэтому применять принцип грубости.

В шахматах партия признается ничьей, если какая-либо позиция возникает в 3-й раз. (По правилам партия в этом случае не обязательно должна быть признана ничьей; она признается ничьей, если этого потребует один из игроков; чтобы избежать бесконечных партий, мы будем считать партию автоматически ничьей при 3-м возникновении одной и той же позиции.) Правила игры не уточняют также того, должно ли при повторении позиции учитываться, занимают ли те же самые фигуры старые места или нет^*. Мы будем предполагать, что позиция считается повторяющейся только при тождественности фигур, занимающих свои старые места.

^* (Я слышал от г-на Уэбба, что в одной из партий Блэкберна позиция повторилась 3-й раз, но пара людей при этом поменялась местами. Каждый из противников играл на выигрыш, но если бы один из них потребовал признать партию ничьей, то возник бы тонкий вопрос интерпретации правил судьей соревнования (как заметил сам Блэкберн))

Какова вероятность того, что игрок А, незнакомый с правилами игры, победит чемпиона мира С^*? Предположим, что С проигрывает одну из n сыгранных им партий, и притом не более чем в m ходов. Предположим, далее, что А знает лишь, что, делая ход, он должен переставить одну из своих фигур на свободное поле или на поле, занятое вражеской фигурой (со взятием). Если А имеет N≤16 фигур, то число его возможных ходов не превышает N^64-N≤M = 10⁴⁸; поэтому вероятность его победы не меньше, чем 1:nМ^m. Число n почти не имеет значения, если мы можем хотя бы немного понизить m; если мы допустим, что m = 20 при n = 10⁶², то шансы А на выигрыш больше, чем 1:10¹²² = ¹/_N1,21 (т. е. выигрыш более вероятен, чем проведение двух извилистых линий из п. 9 подряд).

^* (Мы можем считать, что С (видя игру А в этой партии) не подозревает, что его противник не умеет играть, и сдается, как только он убеждается в неизбежности поражения.)

Каково число возможных шахматных партий? Легко указать верхнюю грань. Любое расположение фигур и пешек на доске (независимо от того, законно ли оно, т. е. совместимо с правилами или нет) мы будем называть расстановкой А; любую законную расстановку - позицией Р. Замену одной расстановки А другой мы будем называть переходом, а законный шахматный ход в позиции Р - ходом. При общем числе N фигур и пешек на доске число возможных А равно ^64!/_(64-N)! (считая пешки различимыми "индивидуальностями" и т. д.). Так как все пешки могут превратиться в фигуры, то это число близко к числу возможных Р (во всяком случае, для некоторых N); основные запреты здесь состоят в том, что короли не должны стоять на соседних полях и не должны быть оба одновременно под шахом и что при наличии 10 белых (или черных) слонов они не должны все стоять на полях одного цвета. Число наборов, состоящих из пешек и пешек, превратившихся в ферзей, ладей, слонов и коней (независимо от их расположения на доске), равно

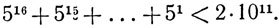
Так как 2 короля обязательно должны быть в наличии, то число наборов фигур, не бывших пешками, равно

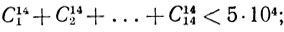
поэтому число всех возможных наборов из N фигур и пешек для любого N меньше 10¹⁶.

Число возможных ходов в данной позиции Р (или даже A) не превосходит

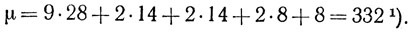
¹⁾ (Рассуждение автора приводит к меньшему числу, чем 332; впрочем, в силу принципа грубости это не влияет на результат.- Примеч. пер.)

Число всех А меньше

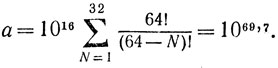
Число возможных партий не превосходит

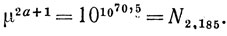
Задача нахождения не слишком грубой нижней грани (пусть даже без полного доказательства, но с субъективной уверенностью) представляется далеко не простой. Число позиций, определяющее верхний показатель, очень быстро растет с N, так что ограничение малыми N ведет к сильно заниженным результатам; если же число N фигур и пешек не мало, то трудно обеспечить их законное участие в позициях, возникающих после длинной цепочки ходов. Можно было бы попытаться ограничиться королями в углах, защищенными тремя легкими фигурами, и несколькими ферзями с каждой стороны (если это проходит, девятью). Эта мысль пришла мне в голову слишком поздно, и я не мог развить ее до каких либо количественных оценок; может быть, кто-нибудь из читателей захочет найти рекордную оценку снизу?

11. Перейдем теперь к числам, о которых я говорил, что они косвенным образом связаны с повседневной жизнью. Они возникают из колоссального числа n₀ = 3*10¹⁹ молекул в 1 см⁴ газа, находящегося в обычных условиях, и соответствующего числа перестановок. Я напомню замечательный пример, приведенный Джинсом: каждый раз, когда кто-либо из нас делает вдох, весьма вероятно, что в его легкие попадают некоторые из молекул, участвовавших в предсмертном вздохе Юлия Цезаря.

Какова вероятность того, что рукопись Гамлета (не печатный текст) возникла случайно? Иными словами, какова вероятность того, что каждая из n молекул чернил, повинуясь случаю, нашла свой путь из чернильницы в некоторую точку чернильной линии, составляющей разборчивую рукопись Гамлета? Мы можем выбрать половину молекул уже расположенными на этой линии и определяющими узкую полосу, в надлежащие места которой должны попасть остальные ¹/₂ n молекул. Если f - вероятность попадания одной молекулы, то интересующая нас вероятность равна f^1/₂n. Так как n - число порядка

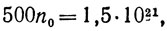
то применим принцип грубости, и будет f равно 10^-1 или 10^-10, большой роли не играет. Искомая вероятность равна ¹/_N2,13

Мы представляем себе, конечно, что произошло нечто значительно менее вероятное: чернильная линия возникла в результате упорядоченной во времени последовательности событий. Каков же дополнительный множитель? Если мы - назовем количество чернил, содержащееся в точке, чернильной точкой, то линию можно считать содержащей, скажем, s = 10⁶ таких точек. Мы должны уменьшить вероятность в s! раз, что оставляет полученную вероятность почти без изменения (условие, выраженное выше курсивным "некоторую", точно так же не оказывает никакого влияния).

12. Мы все знаем, что закипание чайника, поставленного на плиту, представляет собой лишь вероятное, но не достоверное событие. Попробуем оценить вероятность того, что целлулоидная мышь выживет неделю в аду (или, что то же, что живая мышь замерзнет там). Благочестие требует, чтобы мы рассматривали эту задачу в классическом смысле и считали плотности земными. Примем (абсолютную) температуру ада (не желая относиться к этому учреждению без должного уважения) равной 2,8*10¹² = Т_ада (множитель 2,8 я принимаю для облегчения вычислений).

* Пусть с - скорость движения молекул, соответствующая температуре Т, T₀ = 280 (обычная для Англии комнатная температура), с₀ = с(Т₀), c_ада = c(T_ада). Пусть μ = kn₀ - число молекул в мыши (например, k = 10³). Вероятность р того, что данная молекула имеет скорость с≤c₀, равна, в обычных обозначениях,

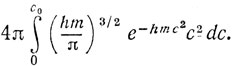
Это - величина порядка

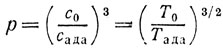
(константа несущественна в силу принципа грубости). Вероятность того, что для большей части мыши с≤с₀, не намного больше, чем p^μ. Пусть τ будет "время релаксации" при температуре Т; это время сравнимо с временем свободного пробега. Тогда

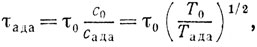
где τ₀ - величина порядка 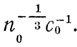В неделе содержится v = ^ω/_τада интервалов продолжительности τ_ада, где ω - число секунд в неделе.

Таким образом, исключительное состояние утрачивается за время порядка τ_ада и для выживания мыши требуется новое "чудо" в следующем интервале. Величина, обратная вероятности выживания в течение недели, имеет поэтому порядок

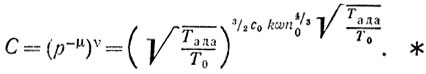
Подставляя численные значения

n₀ = 3*10¹⁹, k = 10³, с₀ = 4*10⁵, ω = 5*10⁵,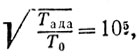

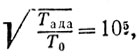
получим

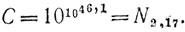
Показатель 46,1 складывается из 5 единиц за счет T_ада/T₀, 5,7 - за счет w, 5,6 - за счет с₀, остальное (основная часть) - за счет n₀.

13.Факторизации. Давно прошли те дни, когда доказательства того, что данное число является простым (или, наоборот, составным), проведенные иначе, чем делением на простые числа до квадратного корня из данного числа, вызывали всеобщее изумление; большинство читателей уже слышало, вероятно, об электрическом сите Лемера, и по крайней мере некоторые из них знают, что "обратная теорема Ферма" сильно продвинула теорию признаков простоты^*. Для сравнения с другими встречавшимися нам числами напомню лишь, что 2¹²⁷ - 1 ≈ 10³⁸ - наибольшее известное простое число^**. 2²⁵⁷ - 1 ≈ 10⁷⁶ - составное число, хотя ни одни из его (собственных) делителей неизвестен: оно является в этом смысле рекордным; 2²⁶ + 1 ≈ 10¹⁹ имеет делители 274 177 и 67 280 421 310 721. Большинство изученных чисел имело, конечно, какую-либо специальную структуру, например, aⁿ ± bⁿ; такие числа допускают применение специальных признаков, основанных на "обратной теореме Ферма". Я спросил профессора Лемера, для каких по величине чисел N можно, скажем, в течение одного года установить, простые они или составные.

^* (Math. Ann.- 1934.- V. 109.- P. 661-667; Bull. Amer. Math. Soc.- 1928.- V. 34.- P. 54-56; Amer. Math. Monthly.- 1936.- V. 43.- P. 347-354.)

^** (Эти данные сильно устарели, что отмечается и ниже в тексте. Рекорды в этой области долго не держатся, и число Лемера (см. с. 115) также уже не наибольшее известное простое.- Примеч. пер.)

• (a) совершенно точно,
• (b) с разумной степенью уверенности,
• (c) при особой удаче^*. ^* (<Ответы на эти вопросы должны быть сейчас пересмотрены в свете использования электронных вычислительных машин.- Пример пер./comment>)

Многое зависит от природы N-1. Если известны достаточно большие делители N-1, то при помощи "обратной теоремы Ферма" можно определить характер N, если число его знаков лежит между 50 и 100. Аналогичные результаты могут быть получены, если известны большие делители N+1. Числа N-1 и N+1 имеют, вообще говоря, много мелких делителей, из которых можно составить достаточно большие делители. "Катастрофические" числа, для которых N, N-1 и N+1 трудно поддаются факторизации, встречаются исключительно редко (этот вопрос заслуживает теоретического рассмотрения). Если же попалось именно такое число, то можно вычислить, например a^N-1 (mod N) для a = 2. Если результат отличен от 1, то число N - составное, обратно, если N - составное, то, как мы можем судить по малым N, до порядка 10¹⁰ очень вероятно, что этот признак даст ответ (хотя это и не обязательно). В случае же, когда

то весьма вероятно, что N является простым (хотя и это не обязательно). В этом случае для окончательного доказательства ничего не остается, кроме "прямых методов", а они применимы примерно до 10²⁰.

Профессор Лемер далее сообщил мне, что числа до 2,17*10⁶ могут быть полностью разложены на простые множители за 40 минут; числа до 10¹⁵ - за один день; наконец, числа до 10¹⁰⁰ при некоторой удаче - за год.

В настоящее время в игру вступили электронные вычислительные машины. Рекордным простым числом теперь является 180 з²+1, где р - предыдущее рекордное число 2¹²⁷-1. После 7 неудачных попыток с другими числами вида kp² + 1, приведенный результат, где k = 180, был недавно получен Дж. С. П. Миллером и Д. Дж. Уилером на машине EDSAC в Кембрижде. Применялся признак, основанный на "обратной теореме Ферма"; вычисления продолжались 27 минут.

Самое последнее известие (апрель 1956 г.): Лемер сообщает свой новый рекорд: 2²²⁸¹-1 простое^*.]

^* (В настоящее время и этот рекорд побит: наибольшим известным простым числом (лето 1960 г.) является 23?17-I,- Примеч. пер.)

^*14. π(х) - lix и число Скьюиса. Разность d (х) = π(х) - lix:, где π(х) - число простых чисел, не превосходящих х, a lix - интегральный логарифм отрицательна для всех х до 10⁷ и для всех х, для которых π(х) известно. Я доказал в 1914 г., что должно существовать такое X, что d(x) положительна для некоторого х≤Х. Впоследствии выяснилось, что мое доказательство является чистым доказательством существования, и из него не может быть извлечена никакая численная оценка Х; такая оценка, свободная от всяких гипотез, была найдена д-ром Скьюисом в 1937 г.; его работа еще не опубликована, хотя, по-видимому, ее публикация не должна заставить себя долго ждать. Пока же я изложу некоторые соображения по этому поводу, так как, кроме значения X, мы встретимся здесь и с другими неожиданностями.

Если мы обозначим θ точную верхнюю грань вещественных частей комплексных корней дзета-функции Римана ζ(s), то знаменитая гипотеза Римана (г. Р. для краткости) состоит в утверждении, что θ = ¹/₂; если это неверно, то ¹/₂<θ≤1. Уже давно было известно, что в последнем случае d (х)>х^θ-ε для произвольно малых положительных и сколь угодно больших х, так что в этом случае существование X обеспечено. Отсюда вытекает, что для целей доказательства существования мы можем принять г. Р., и в моем первоначальном доказательстве я так и поступил. Для нахождения численной оценки X также целесообразно начать с принятия гипотезы Римана. На этом пути д-р Скьюис сумел получить результат^*

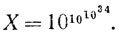
(1)

^* (J. London Math. Soc.- 1933.- V. 8.- P. 227-283.)

Здесь оказалось возможным свести задачу к соответствующей задаче относительно функции ψ(x), связанной с 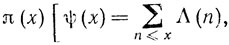есть ln р, если n - простое число р или степень р, и Λ(n) = 0 в остальных случаях]. Для этой задачи соответствующий результат состоит в том, что

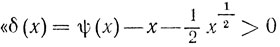
для некоторого x≤X";

если δ(x)>0 для некоторого х, то, грубо говоря (я опускаю детали), d(x)>0 для того же х. Кроме того, мы имеем (вне зависимости от того, справедлива г. Р. или нет) "явную формулу"

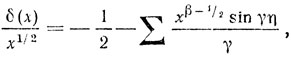
(2)

где β + iγ пробегает все комплексные корни ζ(s) с положительными γ, a η = ln x. Далее, независимо от справедливости г. Р., ряд в формуле (2) может быть оборван, когда γ достигает величины x³, так как допускаемая при этом ошибка пренебрежимо мала.

После этих предварительных замечаний мы можем приступить к рассмотрению основной задачи численной оценки X, свободной от гипотез, и описанию основных этапов ее решения (при этом нам не удастся избежать небольших повторений того, что уже говорилось).

(I) Предположим справедливость г. Р. Тогда β = ¹/₂ и задача состоит в том, чтобы найти Х = Х₀ такое, что

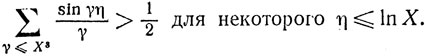
Решение этого неравенства, требующее очень тонких и сложных выкладок, дано в цитированной работе д-ра Скьюиса. Как уже отмечалось, далее должен быть осуществлен хорошо известный переход от ψ к π (от δ к d); X₀, к которому мы приходим, есть число (1).

(II) Известно, что

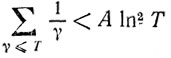
(это - точный порядок). Если вместо г. Р. мы примем несколько более слабую гипотезу, а именно, что ни один корень ζ(s) с γ<X₀³ не имеет вещественной части

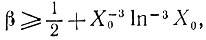
то

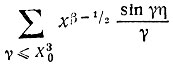
при x≤X₀ отличается от

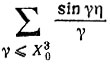
настолько мало, что мы (после тривиальных преобразований) придем к прежнему заключению "δ(x)>0 для некоторого х<Х₀".

(III) Остается доказать существование (нового) X в предположении, что гипотеза п. (II) неверна. Это эквивалентно предположению, что существует корень β₀ + iγ₀, лежащей правее прямой Re s = ¹/₂ на расстоянии не меньшем, чем b = Х₀^-3ln^-3Х₀, и не выше, чем X³₀; тем самым β₀ - ¹/₂≥b и 0≥¹/₂ + b, так что какое-то X существует. Но мы встречаемся здесь с новой неожиданностью. Имея корень β₀ + iγ₀, определенный выше, мы вправе ожидать, что исходное θ-рассуждение приведет к какому-то зависящему от этого корня значению х, для которого δ(x)>x^θ-ε; иначе говоря, казалось бы, что для некоторого х ряд

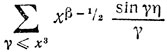
должен превосходить, скажем, 1/10 величины его члена x^{β₀-1/₂sin γ₀η}/_γ0 (причем синус должен быть положительным). Д-р Скьюис убедил меня, однако, что такого вывода сделать нельзя: трудность заключается в том, что в ряде могут найтись для каждого выбранного члена другие члены того же или большего порядка, погашающие этот член. Эта трудность далеко не тривиальна, и для ее преодоления нужна новая идея. В конце концов мне удалось в общих чертах ее I найти.

(IV) Но с задачей еще не покончено. Д-р Скьюис убедил меня (на этот раз преодолевая мое сопротивление), что без г. Р. уже невозможно сделать переход от ψ к π. Поэтому оказывается необходимым проводить все выкладки с использованием явной формулы для π(х) вместо ψ(x), что влечет за собой немало дополнительных трудностей. Д-р Скьюис проделал все это и получил окончательный результат Х = N₄(1,46) (улучшено до N₃(3)).*

15. В связи с только что рассмотренной задачей возникает следующий вопрос: возможна ли ситуация, когда существование числа X доказано, но численная оценка X не может быть дана вследствие того, что возможные значения X столь велики, что не могут быть указаны? Математик даст на этот вопрос отрицательный ответ, но мы тем самым возвращаемся к вопросу, с которого мы начали: сколь большие числа можно вообще записать? Речь фактически идет о том, чтобы построить функцию F(n), растущую чрезвычайно быстро; что мы затем подставляем вместо n: число 2, или u, или N_u(u), уже не составляет большой разницы. (Мы должны где-то остановиться в построении F(n), но еще одна итерация F(F(n)) перевесит все различия в подставляемых значениях n.)

Мы исходим из строго возрастающей положительной функции f = _f(n). Если мы условимся писать ψ^k(n) вместо k-й итерации ψ(ψ(... ψ(n))), то положим

(число показателей равно f₀(n)), где индекс нуль всюду опущен.

Это построение определяет переход от индекса 0 к индексу 1. Аналогично через f₁ определяется f₂(f₂(n) = f₂(n, f₁)) и т. д. Воспользовавшись идеей обозначения трансфинитных порядковых чисел, образуем теперь

(с f_n(n) индексов). Теперь поступим так: забудем все наши промежуточные обозначения и обозначим последнее выражение через f₁(n), после чего продолжим наше построение, вновь забудем все промежуточные обозначения и т. д.; но здесь я предпочитаю остановиться. Теперь положим, например, f₀(n) = n² или n + 1 (каково f₀(n), не играет никакой роли, лишь бы имело место неравенство f₀(n)>n).

Читатель согласится с тем, что записанные нами числа велики; трудно представить себе, однако, сколь они велики; все, что про них можно сказать,- это то, что они своим определением заданы. Если бы понадобилось сравнить два числа двух конкурирующих систем, то для этого пришлось бы создавать солидный математический аппарат.