Ньютон и притяжение шара

(Перепечатано из Mathematical Gazette.- July 1948.- V. 32, N. 300.)

1. В статье Кейнса, опубликованной в сборнике Newton Tercentenary Celebratibns, есть такие абзацы:

"Мы имеем свидетельства, что при подготовке своих Principia Ньютон почти до последнего момента не располагал доказательством того, что с материальным шаром можно обращаться так, как если бы вся его масса была сосредоточена в центре; это доказательство он нашел не ранее, чем за год до опубликования. Но в справедливости самого факта он был уверен многие годы, и всегда применял его.

Не подлежит сомнению, что геометрическая форма, которую Ньютон выбрал для изложения в Principia, не имеет ничего общего с действительным ходом мыслей, который приводил Ньютона к его заключениям. Я думаю, что его эксперименты являлись не столько источником его открытий, сколько проверкой того, что он уже знал".

Интуитивное познание присуще и более скромным умам, а Ньютон обладал им, конечно, в исключительно высокой степени; но я был бы склонен сомневаться в этом конкретном примере интуиции, даже и при отсутствий каких бы то ни было данных. Многие вещи вообще недоступны интуиции, например значение 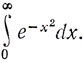"Центральное" притяжение шара, быть может, интуитивно более постигаемо, но в действительности сам Ньютон говорит в своем письме к Хэлли от 20 июня 1686г., что в 1685 г. он считал невозможной замену шара точкой (по поводу этого см. Rouse Ball.An Essay on Newton's Principia, с. 61). Мне кажется поэтому, что есть достаточные и вполне понятные основания, объясняющие, почему Ньютон нашел доказательство этого факта столь поздно. Представляет интерес анализ математической формулировки задачи.

2. Я считаю доказанным, что Ньютон не верил в центральное притяжение до 1685 г. Раз это так, то он вполне мог считать определение фактического притяжения второстепенным вопросом, который можно будет рассмотреть позднее. В конце концов он приступил к решению этой задачи. Теперь, когда мы знаем ответ, задача сводится к отысканию притяжения сферической оболочки, что в декартовых координатах приводит к интегрированию функции (ax+b)/(cx+d)^3/₂ - детская игра для Ньютона. Без знания ответа естественнее идти прямо от полного шара; это приводит к математически более трудной задаче, которая, пока Ньютоном не были полностью разработаны методы анализа, могла поставить его в тупик. В 1685 г. и эта задача была ему вполне по силам. Не исключено (но это можно высказать только в порядке предположения), что он пробовал подойти к решению, рассматривая сначала оболочку радиуса r с последующим интегрированием по r, тогда результат получался сразу. Так или иначе, доказательство было им найдено (и после этого он всегда работал только с оболочками). Но для него это еще далеко не было полным решением вопроса. Как мы теперь знаем, ему нужно было доказательство несомненно аналитическое, но такое, которое можно было бы "перевести" на геометрический язык. Пусть читатель попробует это сделать.

Мне кажется, что я могу с некоторым правдоподобием восстановить аналитическое доказательство Ньютона, и я привожу его здесь в современной трактовке. В нем мы исходим, конечно, из оболочки.

^*3. Рис. 18 принадлежит Ньютону, я добавил только пунктирную линию SH и обозначения трех углов.

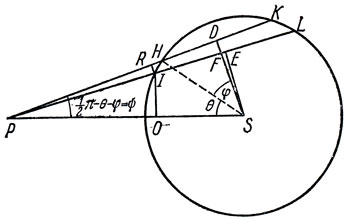
Рис. 18

Пусть SH = a, SP = r. В качестве переменной интегрирования возьмем φ^*. Рассмотрим сферический пояс, образованный вращением HI вокруг SP и его вклад δF = δF_p в общее притяжение F_p точки Р. Этот вклад удовлетворяет соотношению

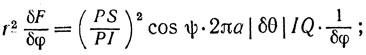
или

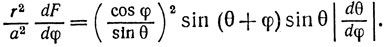
(1)

^* (Алфавитный порядок обозначений приведен в соответствие с положительным приращением δφ.)

Из треугольника PHS находим

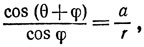
откуда следует, что

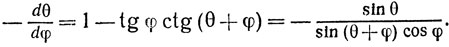
(2)

Из соотношений (1) и (2) заключаем, что

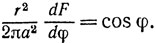
Область R изменения φ есть интервал от -^π/₂ до +^π/₂, и мы получаем результат простым интегрированием. Идея Ньютона состоит в том, что R не зависит от Р, так что для двух положений Р и р мы имеем^*

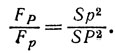
^* (Это и есть утверждение основного положения "Prop 71", Постоянная фактически так и не была никогда определена.)

4. Переходим теперь к геометрическому доказательству (которое, по-видимому, оставляло читателей в состоянии беспомощного восхищения). Имеется второй экземпляр рисунка с малыми буквами (сферы будем считать равными). Интегрирование по φ переводится на геометрический язык следующим "странным" образом: "пусть phk отсекает дугу hk, равную дуге НК, и аналогично для pil. Следующие за этим рассуждения исключительно изящны и проводятся в очень продуманной последовательности, но архаичность языка делает их для нас трудно доступными; поэтому я их модернизирую. Трудности возникают в связи с соотношением (2), которое, естественно, не так легко "перевести".

Так как hk = HK и il = IL, то мы имеем

Вклады δF_p и δF_p двух соответствующих поясов HI и hi удовлетворяют соотношению

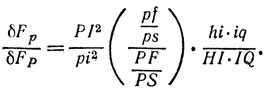
(5)

Кроме того,

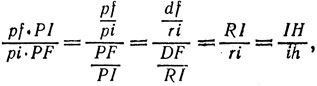
(6)

так как 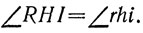Из равенства 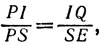соответствующего равенства в малых буквах и равенства SE = se находим, что

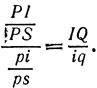
(7)

Перемножая формулы (6) и (7), получаем соотношение

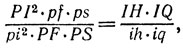
которое в силу равенства (5) приводит нас к равенству

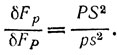
5. Существует доказательство, удовлетворяющее всем требованиям Ньютона, которое, можно полагать, и он нашел бы, если бы раньше не обнаружил другого пути. Оно легко возникает из современного подхода к решению и оперирует сразу с шаром; оно состоит в следующем (мы сохраняем исходные обозначения Р, S).

Рассмотрим ∑ - сферу, концентрическую с данной и проходящую через Р, нормальную к ∑ в точке Р "оставляющую N_Q(P) притяжения единичной массы, помещенной в точке Q, и среднее 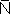_Q составляющих N_Q(P) по всем P на ∑. Величина 4πa²N_Q (среднее, умноженное на площадь) составляется из вкладов всех элементов площади 623; каждый такой вклад, как вытекает из простых геометрических соображений, равен телесному углу, под которым элемент δ∑ виден из точки Q. Поэтому должно иметь место равенство 4πa²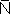_Q = 4π, т. е. 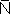_Q не должно зависеть от Q, и таким образом должно быть равно 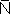_S. Но ∑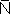_QδV_Q, где сумма распространяется на все элементы объема шара, есть среднее нормальных составляющих притяжения шара по всем точкам ∑, а равное ему выражение 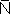_S∑δV_Q является соответствующим выражением для массы, сосредоточенной в S. В обоих случаях усредняемая величина постоянна и равна полному притяжению, и доказательство завершено.

6. Вернемся к вопросу об "интуиции". Естественным аргументом "против" является следующий: "Почему закон обратных квадратов должен занимать такое исключительное место по сравнению, например, с законом обратных кубов?" На это есть ответ: обратные квадраты представляют "естественный" закон убывания с расстоянием, например, освещенности или слышимости и, кроме Ньютона, многие другие думали о нем в связи с планетной системой^*. Или примем корпускулярную теорию света, в которой частицы из разных источников не сталкиваются. Если допустить, что эти частицы не обладают упругостью, то, испускаемые точечным источником, они дают эффект отталкивания, подчиненный закону обратного квадрата, и полное давление на сферу с центром в источнике не зависит от радиуса сферы. Этот факт, в сочетании с симметрией, может вызвать интуитивное ощущение, что ситуация в задаче о притяжении шара делает предположение "центральности" правдоподобным. Но теперь уже рукой подать и до приведенного выше доказательства. Рассмотреть полное давление изнутри (т. е. нормальное давление) на ∑, оказываемое частицами, исходящими из источника Q,- не столь уж сложная идея, и остается только доказать основной факт, что оно не зависит от положения Q.*

^* Заметим, что, как легко видеть, при законе r^-2 притяжение на поверхности шара меньше центрального притяжения, а при законе r^-4 оно больше. Во втором случае это очевидно потому, что соответствующее притяжение бесконечно.