Рецензия на Собрание сочинений Раманужана

(Collected Papers of Srinivasa Ramanujan) / Ed. G. H. Hardy, P. V. Seshu Aiyar and В. М. Wilson.-1927.- XXXVI+ 355 p.

(Опубликовано в Mathematical Gazette.- April 1929.- V14, N 200.)

Раманужан родился в Индии в декабре 1887 г., приехал в Кембридж и начал работать в Тринити-колледже в апреле 1914 г., был болен с мая 1917 г., вернулся в Индию в феврале 1919 г. и умер в апреле 1920 г. Он был членом Тринити-колледжа и членом Королевского общества.

Раманужан не имел университетского образования и работал в Индии без чьей бы то ни было помощи до 27-летнего возраста. Когда ему было 16 лет, он случайно познакомился с книгой Kappa Synopsis of Mathematics, и эта книга, получившая теперь широкую известность, о чем ее автор не мог и мечтать, внезапно пробудила в Раманужане все его дремлющие силы. Чтобы иметь представление о развитии Раманужана, необходимо критически рассмотреть содержание этой книги. В ней можно найти весьма полное изложение формальной стороны интегрального исчисления, включая, например, такие вещи, как формула Парсеваля, интеграл Фурье и другие формулы обращения, а также ряд теорем, формулировка которых имеет понятную для специалиста схему: "f(α)=f(β), если αβ = π²". Мы находим в ней также раздел, посвященный преобразованиям степенных рядов в непрерывные дроби. Кроме того, Раманужан прекрасно знал формальную сторону теории эллиптических функций (которых нет в книге Карра). Неясно, откуда он почерпнул эти знания. Но они вместе с содержанием книги Карра и теми сведениями, которые можно найти, например, в Алгебре Кристалла, по-видимому, составляли все его вооружение в анализе и теории чисел. Во всяком случае, несомненно, что он ничего не знал ни о существующих методах суммирования расходящихся рядов, ни о теории квадратичных вычетов, ни о современном ему состоянии вопроса о распределении простых чисел (формулу Эйлера ∏ (1-p^-s)^-1 = ∑n^-s он, возможно, знал, но о ζ-функции он заведомо не имел никакого представления). К тому же он пребывал в полном неведении относительно теоремы Коши и теории аналитических функций. (Это трудно понять, учитывая его хорошее знакомство с эллиптическими функциями; для объяснения достаточно и, как я думаю, необходимо предположить, что его учебником являлась весьма оригинальная и своеобразная книга Гринхилла Эллиптические функции.)

Работы, опубликованные им в течение индийского периода, не содержат его лучших идей, которые он, по-видимому, не был в состоянии удовлетворительно изложить. В начале 1914 г. в письме к Харди (тогда уже работавшему в Кембриджском Тринити-колледже) он доказал, однако, свою несомненную математическую силу и был приглашен в Тринити-колледж, где он смог активно работать в течение 3 лет до своей болезни. (Некоторые весьма характерные для него работы были написаны в период его двухлетней болезни.)

Я не имею намерения подробно обсуждать здесь те работы Раманужана, которые он написал самостоятельно (очень интересная оценка этих работ дана профессором Харди в вводной статье, с. XXXIV). Если мы пока опустим его знаменитую работу, которую он написал совместно с Харди, то его основной вклад в математику, каким бы существенным и оригинальным он ни был с точки зрения общего интереса, должен, как мне кажется, уступить первое место романтике его жизни и математической карьере, его необычайной психологии и, прежде всего, исключительно интересной проблеме, сколь крупным математиком он мог бы стать при более счастливых обстоятельствах. Говоря это, я, конечно, предъявляю к математическим работам самые высокие требования. Но ведь никакие другие применительно к нему неуместны.

Огромный талант Раманужана был чисто формальным. Он жил "в мире формул". Чтобы яснее выразить, что я имею в виду, приведу два примера (выбор второго, быть может, является случайным; первый же обладает неописуемой красотой):

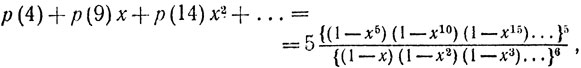
где р (n) является числом представлений n в виде суммы положительных слагаемых;

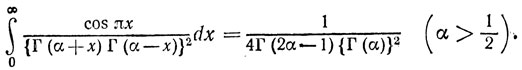
Но времена формул, по-видимому, прошли. Если предъявлять самые высокие требования, то я думаю, что никто уже не будет в состоянии открыть радикально новый тип формул, хотя Раманужан в своих работах, связанных с р(n), был очень близок к этому. Нет смысла умножать число формул Раманужана из круга идей теоремы Коши, теории эллиптических функций и других областей математики, так как в каждой из этих областей в той или иной мере господствует какая-либо общая теория. Лет 100 назад его силы имели бы значительно больший простор. Открытия изменяют общую математическую атмосферу и имеют очень далеко идущие последствия, так что мы не склонны придавать большого значения переоткрытиям, сколь бы независимо они ни были сделаны. Как оценить самостоятельное открытие уже известных математических фактов? Сколь крупным математиком был бы Раманужан, если бы он жил 100 или 150 лет назад? Что мог бы он свершить, если бы он своевременно познакомился с работами Эйлера? Насколько важна недостаточность математического образования? Состояла, ли главная сила Раманужана в выводе формул, или он развивался в этом направлении только благодаря книге Карра (нельзя забывать о том, что он впоследствии научился хорошо делать и другие вещи, и притом в возрасте, достаточно зрелом для индийца)? Такие вопросы возникают в связи с именем Раманужана; в распоряжении каждого имеется теперь достаточный материал, чтобы судить о них.

Наиболее ценными свидетельствами, которыми мы располагаем, являются письма и списки результатов, сообщенных им без доказательств, имеющиеся в собрании его сочинений. Эти свидетельства заставляют предполагать, что его записные книжки дали бы еще более определенную картину сущности его математического гения, и следует очень пожелать, чтобы проект их полного опубликования был в конце концов претворен в жизнь^*.

^* (Записные книжки Раманужана были изданы в 1957 г. (Notebooks of Srinivasa Ramanujan.- V. I-II.- Bombay, 1957.- Примеч. пер.))

Совершенно очевидно, что книга Карра дала Раманужану и общее направление, и зачатки многих дальнейших глубоких его работ. Но даже учитывая это, нельзя не удивляться глубине, разнообразию и силе его таланта. Вряд ли существует область формул, за исключением формул классической теории чисел, которую бы он не обогатил, и в которой он не открыл бы новые, совершенно не подозревавшиеся ранее возможности. Красота его результатов, единственных в своем роде, совершенно поразительна. Не являются ли они даже более необычайными, чем специально подобранная коллекция уникумов? Мораль, по-видимому, такова, что наша фантазия недостаточна; во всяком случае, читатель Раманужана постоянно переживает радостное изумление, и если он пожелает доказать какой-либо наугад взятый недоказанный результат, то - если он вообще будет в состоянии его доказать - он обнаружит по меньшей мере некоторую "изюминку", какой-то новый и неожиданный поворот. Профессор Ватсон и г-н Прийс взялись за героический труд доказать все недоказанные утверждения Раманужана; некоторые из их решений были недавно опубликованы в журнале Лондонского математического общества, и эти работы с несомненностью подтверждают то мнение, что полный анализ записных книжек Раманужана оказался бы чрезвычайно плодотворным.

Не подлежит сомнению, однако, что наиболее удивительные и оригинальные результаты и наиболее глубокое проникновение в существо вопроса обнаруживаются в работах Раманужана по распределению простых чисел (см. с. XXII-XXV, XXVII, 351, 352). Задачи, рассмотренные им в этих работах, по своему существу совсем не формальны; они связаны с приближенными формулами для таких функций, как число простых чисел, меньших данного числа, или число целых чисел, представимых в виде суммы двух квадратов и меньших данного числа; определение порядка остаточных членов составляет в этих задачах главную часть теории. Все эти вопросы имеют очень тонкую теоретико-функциональную основу, и Раманужан неизбежно должен был здесь потерпеть неудачу, так как его методы не могли не увести его в неверном направлении; он выводит приближенные формулы, но его утверждения относительно порядка остаточных членов очень далеки от истины. Эти проблемы напрягали до предела все ресурсы анализа и для своего решения потребовали более ста лет; они вообще не были решены до 1890 г. Для Раманужана полный успех был здесь заведомо недостижим. Он понял только, что за решение этих проблем можно приняться с формальной стороны, и продвинулся настолько, что смог угадать основные результаты. Соответствующие формулы являются очень глубокими, и его достижение в целом должно оцениваться как совершенно исключительное.

Если книга Карра дала ему определенное направление в работе, то уж во всяком случае она не имела ничего общего с его методами, наиболее важные из которых абсолютно оригинальны. Его интуиция опиралась на аналогии, часто весьма отдаленные, и в необычайной мере - на эмпирическую индукцию, основанную на числовых примерах. Не имея в своем распоряжении теоремы Коши, он, естественно, много работал с преобразованиями двойных интегралов и обращениями порядка интегрирования в них. Но его наиболее важным орудием, по-видимому, являлась высоко развитая техника преобразований расходящихся рядов и интегралов. (Хотя такие методы хорошо известны, не подлежит сомнению, что он открыл их совершенно самостоятельно.) Он не располагал строгими доказательствами законности своих операций. Он не интересовался строгостью, которая, кстати, в анализе за пределами студенческих работ не имеет первостепенного значения и может быть при наличии настоящей идеи всегда внесена любым компетентным профессионалом. Возможно, что Раманужан вообще не имел четкого представления о том, что сейчас в математике понимается под доказательством. Если существенное, хотя бы и небольшое, рассуждение в сочетании с эмпирическими данными и интуитивными догадками давало ему субъективную уверенность в правильности результата, то больше он ничем не интересовался. Одним из второстепенных признаков его гения является тот факт, что он никогда не ощущал необходимости в чем-либо аналогичном теореме Коши. С ее помощью он дошел бы до некоторых своих результатов гораздо быстрее и проще. Но его собственные методы позволяли ему обозревать весь круг вопросов с такой же полнотой и с такой же уверенностью.

В заключение я должен кое-что сказать об его работе по представлению функции р(n), написанной им совместно с Харди (с. 276-309). Число р (n) очень быстро возрастает с ростом n. Так, например,

Авторы показывают, что р(n) является ближайшим целым числом к

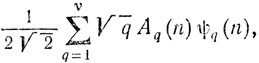
(1)

где

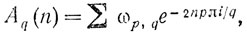
причем сумма распространяется на все р, взаимно простые с q и меньшие q, a ω_p,q - некоторый корень 24-й степени из 1; v имеет порядок √n и, наконец,

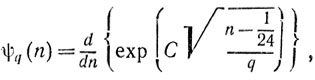
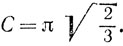
Мы можем принять v = 4, когда n = 100. Для n = 200 можно взять v = 5; 5 членов ряда (1) дают точное значение р(200). Всегда можно положить v = α√n (точнее, целой части α√n), где α - любая положительная постоянная, если только n превышает некоторое число n₀(α), зависящее только от α.

Читателя не нужно убеждать в том, что это очень удивительная теорема; он легко поверит, что методы, при помощи которых она была установлена, содержат новый и важный принцип, оказавшийся чрезвычайно плодотворным и в других областях. История этой теоремы в высшей степени интересна (чтобы воздать ей должное, мне придется несколько нарушить правила соавторства, и поэтому я добавлю, что профессор Харди разрешает мне рассказать о следующих фактах относительно его совместной работы с Раманужаном). Одна из гипотез Раманужана, относящаяся еще к индийскому периоду его жизни, состояла в том, что первый член в формуле (1) является очень хорошим приближением к р(n); это было установлено без большого труда. На этом этапе вместо n-¹/₂₄ фигурировало просто n, но это было пока несущественно. Отсюда начался настоящий штурм задачи. Следующим шагом вперед, не очень большим, было рассмотрение разложения (1) как асимптотического ряда, из которого следовало брать фиксированное число членов (например, 4), причем ошибка имела порядок следующего члена. Начиная с этого момента до самого конца работы Раманужан упорно настаивал на том, что в действительности верно гораздо больше, чем было доказано; он утверждал, что "должна существовать формула с ошибкой O(1)". Эта гипотеза была его важнейшим вкладом, одновременно и чрезвычайно существенным и в высшей степени поразительным. Была сделана точнейшая численная проверка, которая выявила удивительные факты относительно p (100) и p (200).

Тогда v было сделано зависящим от n; это было очень большим шагом вперед и потребовало новых глубоких теоретико-функциональных методов, которые Раманужан, несомненно, не мог бы открыть сам. Теперь, наконец, стала вырисовываться вся теорема. Однако преодоление самой последней трудности было бы, вероятно, невозможно без еще одного вклада Раманужана, на этот раз очень характерного для него. Мало того, что аналитические трудности этой теоремы были громадными,- подступы к ней оказались еще забаррикадированными почти непреодолимыми чисто формальными препятствиями. Вид функции Ψ_g(n) ни на йоту не может быть изменен. Среди многих асимптотически эквивалентных выражений необходимо выбрать одно единственно правильное. Если бы это не было сделано с самого начала (a-¹/₂₄, не говоря уже о ^d/_dn, могла появиться в Ψ_g только в результате исключительно блестящего прозрения формального гения), то эта теорема вообще никогда не могла бы возникнуть. Все это представляется загадочным. Если бы мы знали, что существует формула с ошибкой O(1), то мы постепенно пришли бы в конце концов к правильному виду для Ψ_q(n). Но почему Раманужан был так уверен, что подобная формула существует? Трудно поверить, что это объясняется просто необычайной глубиной проникновения его умственного взора. С другой стороны, трудно представить себе, какие численные примеры могли быть в распоряжении Раманужана, чтобы он мог привычным для него процессом интуитивной индукции прийти к заключению о справедливости столь сильного результата. В то же время, если вид Ψ_q(n) не был известен ему заранее, то никакие численные данные не могли ничего ему подсказать. Так что, по-видимому, единственный возможный вывод состоит в том, что открытие им правильных формул было результатом взлета гения. Эта теорема возникла в результате исключительно удачного сотрудничества двух математиков совершенно разнородных способностей, в котором каждый из них проявил самые сильные, самые характерные стороны своего таланта. В этой совместной работе с Харди гений Раманужана нашел возможность развернуться в полной мере.

Книга содержит биографию, написанную Сешу Айяром, и некролог, составленный профессором Харди. Биография и некролог дают нам живую картину интересной и привлекательной личности Раманужана. Математики, подготовившие это издание, превосходно справились со своей задачей. Труд их почти незаметен: читателю сообщается то, что он хочет знать, и как раз в нужный момент; это потребовало от них больших усилий и большего объема библиографических исследований, чем читатель склонен предполагать.