Математическое образование

Это - мое образование. Оно иллюстрирует общее положение дел до 1907 г., но имеет и свои специфические особенности.

К числу моих слабостей не принадлежит ложная скромность, и я охотно сообщаю, что был очень развитым ребенком. Между прочим, раннее развитие не имеет для математика особого значения, и мы имеем массу примеров как раннего, так и более позднего развития среди математиков. Что касается меня, то я принадлежу к числу рано развившихся.

Я родился 9 июня 1885 г. и жил в Южной Африке с 1892 г. по 1900 г.; в возрасте 14 лет я покинул университет в Кейптауне и спустя 2 или 3 месяца отправился в Англию, чтобы учиться в школе Св. Павла, где в течение 3 лет моим учителем был Ф. С. Маколей. Знания мои по современным стандартам были незначительны: первые 6 книг Евклида, немного алгебры и тригонометрия до решения треугольников. 3 года в школе Св. Павла я занимался очень усердно и в результате переутомления некоторое время находился в состоянии депрессии.

Учебной традицией в те времена (восходящей, в конечном счете, к Кембриджу) было интенсивное изучение "низших" методов до перехода к методам "высшим"; так, аналитические методы в геометрии проходились поздно, анализ - очень поздно. При этом каждый учебник изучался до конца или почти до конца, прежде чем открывался следующий. Была принята такая последовательность учебников: Алгебра Смита; Тригонометрия Лонея; Геометрия конических сечений самого Маколея (довольно трудная книга: например, метрические свойства параболы разобраны в ней с бесконечной виртуозностью); Статика и динамика Лонея, без применения анализа; Аналитическая теория конических сечений Смита; Дифференциальное исчисление Эдвардса; Интегральное исчисление Уильямсона; Гидростатика Безанта. Все эти книги были аннотированы Маколеем и снабжены контрольными работами, которые мы периодически писали. В дополнение к обязательному минимуму каждый мог читать все, что отвечало его индивидуальным вкусам. Мое дополнительное чтение шло, насколько я помню, в такой последовательности: Дополнения к Евклиду Кэзи; Алгебра II Кристалла; Конические сечения Салмона; Тригонометрия Гобсона (2-е изд., 1897); Динамика точки Рауса (более 400 страниц с весьма сложными дополнениями в конце); Динамика твердого тела Рауса; сферическая тригонометрия (со всеми мельчайшими подробностями); Дифференциальные уравнения Мэррея; Стереометрия Смита; Теория уравнений Бэрнсайда и Пэнтона; Статика Минчина (без теории упругости, но с теорией притяжения, сферическими гармониками и, конечно, подробным исследованием притягивающихся эллипсоидов^*).

^* (Излюбленный вопрос в системе английского математического образования, впервые подробно рассмотренный самим Ньютоном.- Примеч. пер.)

Я прочел почти все из этого списка до университетских вступительных экзаменов на стипендию в декабре 1902 г. (Ожидали, что я сдам эти экзамены хорошо, но вопросы в письменных работах были для меня слишком трудными, и я получил только Малую стипендию в Тринити-колледж^*.) За несколько недель до этого у меня был тяжелый грипп, и хотя я не чувствовал себя нездоровым, по-видимому, все же я не был в лучшей своей форме. В школе нас не слишком загружали учебной работой, и мы не слушали лекций; каждый из нас мог в случае каких-либо затруднений обратиться к Маколею, но этого, как правило, никто не делал. Время от времени мы представляли письменные работы,- сначала решения указанных им задач из изучаемой книги, а затем задачи по нашему выбору. (Мы получали еженедельное задание из Вулстенхолмовского сборника, составлявшееся Маколеем, а впоследствии старшим учеником, каковым на последнем году обучения был я сам; если никто из нас не мог решить какую-либо задачу, то обязанностью Маколея было решить ее перед нами на доске.) Классу рекомендовали обращаться -за помощью к отаршим ученикам, что приносило большую пользу всем. Работа по подготовке к экзамену на стипендию заключалась только в повторении материала за предшествующую четверть. (Маколей достиг больших успехов в преподавании. За 25 лет его работы в школе 52 его ученика получили университетские стипендии (из них 34 -в Кембридже); среди них за 20 лет 4 были первыми в своих выпусках из университета, 1 занял второе место и 1 - четвертое. Годы моего учения были в этом отношении годами "пик". Дж. Н. Ватсон, на курс младше меня в школе и в Кембридже, также был первым; между прочим, он был такой же вундеркинд, как и я. Дж. Р. Блэнко-Уайт, на курс старше меня, был вторым в своем выпуске.) Д-р Максвелл Гарнет правильно отметил в своем описании образования, что оно носило университетский характер. Так как от нас ждали уверенности в своих силах, мы по большей части обретали ее, и поскольку сам Маколей был творчески активен (он стал членом Королевского общества в 1928 г.), мы проникались чувством, что занятия математикой являются нормальной человеческой деятельностью.

^* (Я вспомнинаю, как сильно я был расстроен на первом письменном экзамене тем, что напротив меня сидел экзаменующийся, который с большой быстротой разделывался с одной задачей за другой; на следующих экзаменах я уже выбирал другое место. То был, вероятно, Мерсер (который окончил до этого Манчестерский университет и начинал в Кембридже все сначала, что в те годы довольно широко практиковалось). Я помню также, что Кембридж внушал мне такое благоговение, какого я уже никогда больше в жизни не испытывал.)

До сих пор мое образование протекало правильно, а отдельные его недостатки коренились в самой системе. Было бы лучше учить анализ по французскому Cours d'Analyse, а не по Кристаллу и Гобсону, но это было бы в высшей степени необычным. Я не считал себя математиком (и, тем более специалистом в области анализа) до тех пор, пока я не сдал первый экзамен в университете, но я обладал инстинктивным интересом к математической строгости и легко одолевал главы из Кристалла о пределах и сходимости. Книга эта написана строго (в разумных пределах); тем не менее, я по-настоящему понимал, например, равномерную сходимость, хотя и достиг этого с большим трудом. (2-е издание Гобсона, 1897 г., представляет собой, По замечанию Маколея, странное сочетание придирчивой строгости с удивительными промахами^*, которые, однако, меня, проработавшего "сходимость" по Кристаллу, не вводили в заблуждение.)

^* (Например, неверное доказательство того, что два степенных ряда, принимающих одинаковые значения, имеют одни и те же коэффициенты. На с. 243-244 мы также находим странные абзацы: "Если предел S_n бесконечен или если он конечен, но не определен, то ряд расходится"; "Чтобы доказать достаточность [общего принципа сходимости], обозначим через R_n бесконечный ряд a_n+1 + a_n+2 + ..., остаток после n членов; устремляя r к бесконечности [в ∑^n+r_n+1], мы видим, что |R_n|<ε, если n≥m, и, следовательно, значение S заключено между S_n ± ε [a ε произвольно мало]; с другой стороны, S_n является суммой некоторого числа конечных величин, а поэтому само конечно. Таким образом, S_n+r - S_n может быть сделано сколь угодно малым, если выбрать n достаточно большим; следовательно, lim S_n = lim S_n+r. и значение S определено, так как оно не зависит от формы n". [Для сокращения сделаны тривиальные изменения.]* Когда Гобсон это писал, он уже был специалистом в области анализа. Мы имеем здесь один из наиболее ярких примеров слепых пятен и слепого следования традиции при написании учебника: никто не может подвергать сомнению каждое написанное им слово. Я однажды поймал себя на том, что на лекции автоматически привел очень плохой признак законности дифференцирования под знаком интеграла, в то время как мне был известен гораздо лучший признак, который я, несомненно, использовал бы в работе.)

Но с этого момента (после экзамена на стипендию) я начал растрачивать свое время, за исключением редких периодов интенсивной работы; это длилось около 2 ¹/₂ лет (последние 8 месяцев в школе и 2 академических года в Кембридже). Сначала о 8 месяцах в школе. Первое время после экзаменов я, правда, читал Стереометрию Смита; это не заняло много времени, но я припоминаю, что хотя я быстро во всем разобрался, к экзамену по этому материалу я не был готов и на выпускных экзаменах в школе не мог решить некоторых задач. Из вопросов прикладной математики лучше всего было выбрать "воду, газ и электричество". Подходящего учебника по электричеству, по-видимому, не было, но зато имелась Гидродинамика Ламба. Я очень долго (по собственной оплошности) изучал динамику и дошел до вопроса о движущейся системе координат. По чистой математике идеалом было бы чтение какого-нибудь полного Cours d'Analyse. Вместо этого я потратил массу времени на чтение книги Тэта, посвященной бесполезной теме о кватернионах. Затем наступил один из рабочих периодов: я занялся чтением Введения в теорию аналитических функций Харкнесса и Морлея (1898 г.). Здесь следовало бы начать распространяться о бесконечных горизонтах, которые открылись передо мной, и о новом понимании математики, которого я достиг, но фактически дело обстояло несколько иначе. Отдельные вещи^* действительно изумили и потрясли меня, а некоторые из них надолго врезались в мою память^*. Но бесконечные горизонты не открылись. Откровенно говоря, я скептически отношусь к "Введениям": они могут быть У прекрасным чтением, если вы уже знаете предмет, но я не думаю, чтобы они могли увлечь читателя, незнакомого с предметом. Для такого читателя ничто не может заменить подробного изложения со всеми техническими деталями, требующего честной проработки. Между прочим, книга Харкнесса и Морлея несколько запутанно излагает вопрос о действительном числе, но это, вероятно, было неизбежно в 1898 г.; ничто из того, что изучало мое поколение, не обладало той бодрящей четкостью, с которой встречаются студенты сегодня.

^* (Такие, как вычисление определенных интегралов при помощи контурных, что при первом знакомстве производит ошеломляющее впечатление па каждого студента.)

^** (В связи с этим возник один инцидент в первом триместре моего прибывания в Кембридже. Наш лектор по анализу был большим педантом. Однажды на лекции мне было ясно, о чем дальше будет идти речь, так как я хорошо помнил X. и М., поэтому я быстро записал все в своем конспекте и стал демонстративно смотреть в окно. "Вы не собираетесь записывать то, что я говорю, сэр?"- "Я уже ; все записал". Он явно колебался, попросить ли мой конспект для проверки или нет (тогда еще обо мне как о студенте ничего не было известно), но в конце концов сказал: "Прошу прощения". Присутствовавшие в аудитории считали, что я выиграл эту встречу по очкам, но сам я чувствовал, что победа осталась за ним, поскольку я был невежлив.)

Прибыв в Кембридж (октябрь 1903 г.), я в течение 2 лет (20 месяцев^*) готовился к первому экзамену; моим репетитором был Р. А. Герман, друг моего отца и последний крупный репетитор^**. Когда я вспоминаю об этом времени, оно представляется мне довольно мрачным. Если говорить о том новом, что я узнал и что действительно было достойно изучения, то стоит отметить движущуюся систему координат в динамике, гидродинамику и дифференциальную геометрию (сверх того, что есть у Смита), а также небольшие добавления к тому, что я уже знал о сферических гармониках и анализе в комплексной области. Мои знания по электричеству были незначительными и отрывочными; я никогда не видел уравнений Максвелла^***. Энтузиазм у меня вызвали только два курса: в первом триместре заставлявший мыслить курс оснований механики А. Н. Уайтхеда и прекрасный курс дифференциальной геометрии Германа; подробнее об этом я скажу позже. Чтобы претендовать на первое место в своем выпуске, надо было две трети всего времени израсходовать на тренировку в быстром решении трудных задач. Помню, что я не придавал серьезного значения посещению лекций, за исключением лекций Германа; мои конспекты показывают, что я присутствовал примерно только на половине всех лекций, а если я не посещал лекций по какому-нибудь курсу систематически, то больше я уже не заглядывал в конспекты.

^* (Включая только одни Большие каникулы.)

^** (Реформа (1910 г.) почти сразу уничтожила институт репетиторов.)

^*** (Справедливость требует отметить, что я не мог изучать все читавшиеся курсы (в колледже или с репетитором). Для полноты картины следует добавить, что я растратил время на оптику и астрономию (не стоящие изучения) с тем, чтобы после этого забросить их.)

Принято было говорить, что тренировка в "навыках преобразований" приносит позже пользу в исследовательской работе. Я отрицаю это почти безоговорочно - такие навыки далеко не ведут. Мой опыт показывает, что после нескольких лет от них ничего не остается, кроме умения щелкать как орешки экзаменационные задачи (из современных сборников) с маленьким глупым чувством гордости за демонстрируемую виртуозность, которая ценится и по сей день; меня это никогда не заботило в отличие от моих младших коллег. (Я сказал "почти безоговорочно"; существуют редкие исключения. Если бы Герману в удачный момент предложили одно из более замысловатых элементарных неравенств, я легко могу себе представить, что он наметил бы доказательства, близкие к самым современным и самым изящным, а может быть, сделал бы и новые открытия.)

Старая система университетских экзаменов и ее пороки теперь уже ушли в прошлое; я не хочу стегать мертвую лошадь. Я не претендую на роль жертвы, тонкая натура которой не могла в полной мере развиться и зачахла. Я брал жизнь такой, какой она была; игра, в которую мы играли, давалась мне легко, и я даже чувствовал некоторое удовлетворение от своего мастерства.

Подробности моей карьеры за эти 20 месяцев были следующими. В первом триместре я работал слишком много. С другой стороны, я почти не работал во втором триместре (частично из-за подготовки к лодочным гонкам); в результате я принял участие в мартовских экзаменах на Большую стипендию^*, к которым все равно нельзя было как следует подготовиться; чувствуя себя достаточно уверенно, я полностью восстановил свою репутацию, испорченную; провалом на вступительных экзаменах, сдав первым во главе списка. В июне я сдавал майские экзамены за 2-й год и вновь оказался первым (Мерсер эти экзамены не сдавал). Я получил максимальное число очков за задачи из анализа, и это было моим первым знакомством с изумленным Харди, который в это время только начинал свою работу в Тринити-колледже (и частным образом репетировал Мерсера). В течение 2-го года моего обучения единственным академическим событием был экзамен, где я разделил первое место с Мерсером (мне тогда еще не было 20 лет).

^* (Это были конкурсные экзамены, открытые для всех; сейчас они отменены.)

Майские экзамены по анализу напоминают мне один мой неумный эксперимент, и я остановлюсь на нем. Я жил в Байдфорде (Дэвбн) и решил провести часть пасхальных каникул, забравшись в Хартленд Кей (чудесная местность и наиболее удаленный от железной дороги населенный пункт Англии). Основная идея состояла в том, чтобы бросить курить, сосредоточенно работать по утрам и после обеда и "отдыхать", читая поэзию и философию (Principia Ethica) по вечерам, подкрепляясь крепким кофе. (Кстати сказать, мое поколение работало главным образом по ночам, и час ночи считался ранним временем для отхода ко сну: существовало чудовищное мнение, что 8 часов - это ежедневный минимум для занятий математикой; истинно добродетельный человек должен был выкраивать за счет сна 10 часов работы в день.) Мое окно "выходило на море, которое я использовал как корзинку для бумаг, и по прибытии я торжественно выбросил в него мою трубку и табак. Однако уже на следующий день я закурил снова. Работал я там без напряжения, занимаясь чтением тех мест из Современного анализа Уиттекера, которые мне еще не были известны, и повторяя все остальное; поэтому-то я и был так хорошо подготовлен по анализу на майских экзаменах. Этот эксперимент показал мне справедливость того правила, что для серьезной работы нет ничего лучше привычных условий и обычного режима и что на отдыхе надо отдыхать. На эту тему можно было бы сказать многое, но здесь не место для этого; скажу, однако, чего мне надо избегать, когда я занят творческой работой: это, в первую к очередь, кембриджской жизни с ее оживленными беседами умных людей - вредными стимулами, отвлекающими мысль в сторону, и товарами, выставленными в витринах.

Кое-что о самих майских экзаменах. Они состояли из 7 работ ("первые 4 дня") на сравнительно элементарные темы, но с довольно сложными дополнительными вопросами, за которыми через неделю ("вторые 4 дня") следовали еще 7 работ. Успешное выполнение работ первых 4 дней давало право сдавать следующие экзамены на степень^*, но работы вторых 4 дней были оценены примерно двойным числом очков, а так как было просто невозможно подготовиться ко всему, то кандидаты на первые места концентрировали свои усилия на подготовке ко вторым 4 дням^**; к тому же в работах вторых 4 дней почти всегда можно было найти достаточно вопросов по основным предметам. Лидеры после первых 4 дней обычно имели примерно одинаковые результаты; вопросы и задачи, с которыми им приходилось иметь дело, теперь кажутся почти невероятными. Все это - потерянный мир, и за исключением отдельных случаев я даже приблизительно не помню, какие задачи мне приходилось решать. Я унаследовал от одного из экзаменаторов ведомость с оценками за мой год (1905). Если исключить работу по решению задач повышенной трудности, то за первые 4 дня лидеры получили 1350, 1330, 1280, 1230 очков (третий и четвертый из них в дальнейшем вышли на первое место); за ними следовали еще 8 лидеров, из которых последний получил 990 очков. Максимальное число очков было 1930, и работы состояли из 10 задач каждая, большей частью с трудными дополнительными вопросами. По задачам повышенной трудности Мерсер получил 270 очков из 760 за 18 задач (я получил только 180). По одной работе я получил 177 очков из 230 за дополнительные вопросы, и об этом я кое-что помню. Один вопрос относился к циклу Карно и требовал только книжных знаний, но я этого вопроса не знал. Другой относился к конденсатору, о котором я тоже ничего не слышал, но мне удалось разобраться в этом вопросе по ответу к дополнительной задаче. Я припоминаю, однако, что я сделал все, кроме вопроса о Карно, так что потерянные мною очки были вычтены за ошибки в арифметических расчетах и вообще за свойственный мне "неряшливый стиль"^***. За вторые 4 дня Мерсер и я (не считая работы с задачами повышенной трудности) получили каждый примерно по 2050 очков из 4500 (по задачам повышенной трудности общим числом 18 каждый из нас получил 1 приблизительно 330 очков из 1340 возможных). Что меня больше всего удивляет в этой ведомости - это то, что я по одной из работ (смешанная работа по чистой и прикладной математике), требовавшей только книжных знаний, получил почти полное число очков (290 из 310, так что я, очевидно, временно избавился от "неряшливости"), плюс 250 очков из 590 за дополнительные вопросы.

^* (Диплом об окончании университета.- Примеч. пер.)

^** (Мне пришлось писать одну очень неприятную работу в первые 4 дня; сплошь оптика и астрономия.)

^*** (Я сам никогда не снижаю очков на экзаменах за неряшливость как таковую (и всегда протестую против лепета экзаменаторов по поводу "неряшливости в выкладках и ошибок в расчетах"). Сумбурное изложение в продуманной рукописи является, конечно, тяжким грехом, но в рукописи, написанной наскоро в экзаменационных условиях, оно простительно. В связи с этим вообще говорилось много глупостей. Я с удовольствием вспоминаю одного человека, который был знаменит ясностью своей мысли и каллиграфическим исполнением экзаменационных работ; его всегда ставили нам в пример. Его дальнейшая карьера ознаменовалась таким числом плохих, запутанных и совершенно неверных математических работ, какого я не встречал ни до, ни после него.)

График распределения очков, полученных на экзаменах, далек от гауссова; от своей высшей точки он идет дальше горизонтально. Это легко понять, но интересно, что соответствующий график для недавних майских экзаменов имеет, грубо говоря, гауссову форму.

Только в отношении еще одной задачи я уверен в том, что решил ее, и именно по следующей причине. Я начал решать задачу по элементарной теории чисел, в которой я чувствовал уверенность со школьных дней. Задача не получалась, я не мог ее решить после ряда попыток. Мне понадобилась еще бумага; проходя мимо других экзаменующихся, я краем глаза увидел жирную галочку против этой задачи в работе одного студента, который никак не принадлежал к числу ведущих, и я подсознательно заключил, что задача должна быть очень простой, так что я напрасно усложнял дело; после этого я сравнительно легко решил ее. Сугубо щепетильный человек не стал бы уже решать эту задачу; я немного жалею, что так не поступил, но слишком больших угрызений совести мой поступок за собой не повлек.

Теперь о втором экзамене (1906 г.). Здесь мы имели , дело с настоящей математикой (этот экзамен, не считая того, что он теперь является третьим и проводится на третьем, а не на четвертом году обучения, остался почти без изменений с 1880-х годов). Много времени я потратил зря, о чем, конечно, можно пожалеть. Однако это являлось, в общем, нормальным явлением, связанным с поисками и ошибками. Продолжая изучение дифференциальной геометрии, я приступил к чтению Теории поверхностей Дарбу и проработал 3 из 4 томов (т. е. в общей сложности 1500 страниц). Это - замечательное произведение, но мой начальный энтузиазм несколько упал: дифференциальная геометрия не была моим призванием. На экзаменах встретилось несколько вопросов из нее, и я на все ответил; но я мог бы ответить на них и на год раньше по лекциям Германа. В остальном мои занятия были посвящены разным вопросам анализа. В деле подготовки будущего специалиста по математическому анализу Кембридж неизменно достигал одного: глубокого знания функций Лежандра и родственных вопросов. Такие предметы справочного характера никуда не годятся для хорошего математика. Обязательность этих знаний обеспечивалась еще и тем, что читался отдельный курс (Э. У. Гобсоном; впоследствии он написал стабильный учебник по этому предмету); я был единственным его слушателем. Я с удовольствием вспоминаю о том, что все эти вещи полностью оставались у меня в памяти: мне пришлось встретить несколько задач по этому разделу на экзамене, и я решил их все без затруднений. Я был также единственным слушателем курса Э. У. Барнса по обобщенным Г- и ζ-функциям. Весьма оригинальный курс читался также Г. Ф. Бэйкером по избранным вопросам из различных областей анализа; этот курс был весьма стимулирующим, но его построение нельзя было назвать педагогичным. Я записался также на более элементарную из двух частей курса эллиптических функций и "слушал" соответствующий курс А. Берри. Лекции Берри начинались в 9 часов утра, и я попадал только на половину из них (поскольку работал до 2-3 часов утра); я никогда не обращался к своему конспекту этих лекций, и я не прибегал также к очевидной альтернативе чтения учебника (хотя в те годы, в отличие от нынешнего времени, студенты в значительно большей степени опирались на учебник, чем на лекционный курс). Поэтому я не собирался сдавать экзамен по этому предмету. Дело в том, что я тогда еще не имел представления о том, чем мне следует заниматься в первую очередь и, в частности, еще не изучил как следует теорию функций комплексного переменного. Приобретя каким-то образом определенные сведения из математического анализа, я еще никогда серьезно не изучал ни одного Cours d'Analyse. Другие математики уже неоднократно отмечали, что впервые они поняли, что такое настоящая математика, только читая Жордана; я это упустил. Но я вообще был в своих занятиях весьма несистематичен; Пикар был бы, несомненно, очень полезен для меня. Все это я помню весьма смутно и, вероятно, я уже давно забыл многое из того, что было мной прочитано. За несколько недель до экзамена, в третьем триместре, мне попались в руки ранние тома серии Бореля; они-то, в сущности, и оказались первыми книгами, по-настоящему взволновавшими меня; ряды с положительными членами, расходящиеся ряды и том, посвященный целым функциям. Знание материала первых 2 книг не имело значения для экзаменов, третью я официально представил как проработанную к экзаменам, но я ее потерял, не мог быстро раздобыть другой экземпляр, и поэтому не отчитывался по ней. Но теперь я уже знал, что мне нужно.

По некоторым особым причинам я могу точно воспроизвести подробности относительно одной работы (пятница, 1 июня 1906 г.), и в свете моей дальнейшей деятельности меня интересует, чего я тогда не знал. В работе было 6 вопросов:

1. Функции Лежандра.
2. Перемножение рядов.
3. Разрывные функции, интегрируемые по Риману.
4. Обращение степенного ряда (с определением радиуса сходимости).
5. Конформное отображение овала на полуплоскость.
6. Эллиптические функции (υ-функции из второй части предмета, по которой я не отчитывался).

Из них единственным вопросом, который я действительно должен был бы знать, был вопрос 1 (по которому я, конечно, получил наибольшее число очков, затратив минимум времени). По правилам игры это давало мне право на полное число очков за всю работу; но в таких случаях студенты всегда нервничали по поводу того, заметят ли экзаменаторы, что ответ на вопрос был действительно исчерпывающим (именно это и является причиной того, что об этой работе я помню все). Кое-что я знал по вопросу 2, но не в той форме, в какой он был поставлен, так что мой ответ был небезупречным. По остальным вопросам я фактически ничего не знал (хотя за 5 лет до этого, в школе, я знал вопрос 2).

Мне сообщили, что я очень хорошо прошел через весь экзамен. Однако я не имел еще права на получение степени^*. В те времена экзамен, сданный на втором году обучения, совершенно не засчитывался и, хотя второй экзамен давал право на степень, если он сдавался на четвертом году обучения, он не давал этого права, если сдавался на третьем году. Впрочем, была предусмотрена возможность исключений (специальным решением Сената), но я только впоследствии случайно узнал об этом.

^* (Речь идет о степени бакалавра, т. е. диплома об окончании университета.- Примеч. пер.)

Существовало 9 экзаменационных классов, от I (1) до III (3). Уровень классов был иногда чудовищно низким, и в 1910 г. эта система экзаменов сгорела в последней вспышке своей славы. Исключительно многочисленный и сильный контингент студентов этого года дал впоследствии 6 хорошо известных профессоров математики и людей, занимавших эквивалентное положение.

Чтобы покончить с лекциями. На четвертом году обучения почти не оставалось таких курсов, которые мне стоило бы посещать. Профессор А. Р. Форсайт читал курс дифференциальных уравнений; это не отвечало моим вкусам. Но я посещал лекции Уайтхеда по основаниям геометрии и основаниям математики, которые читались впервые. Этот курс слушало 3 или 4 человека, но мы находили его очень интересным. (Уайтхед незадолго до этого был избран старшим лектором в Тринити-колледж. В его обязанности входило чтение факультативных курсов. Читавшиеся им в колледже обязательные курсы, за исключением курса о принципах механики, были весьма солидными, но скучными и относились к прикладной математике: математик иногда обязан быть скучным, как, например, Эддингтон в своих лекциях по сферической тригонометрии.) Я не помню, чтобы я посещал еще какие-либо лекции.

Моя исследовательская работа началась, естественно, в Большие каникулы третьего года обучения, в 1906 г. Мой научный руководитель Э. У. Варне предложил мне в качестве темы целые функции порядка 0. Первой задачей было найти асимптотические формулы для функций с простыми нулями вида а_n = еⁿ; аналитические методы, которые он успешно применял к порядкам, отличным от 0, здесь не работали. Между прочим, в связи с этим я познакомился еще с одним знаменитым и важным томом из борелевской серии, Catcul des Aesidus Линделёфа. Упомянутые методы не работали по самым основательным причинам, как это выяснилось в дальнейшем, но предложение Барнса оказалось очень удачным; мне сразу сильно повезло, и я вскоре, переключившись на элементарные методы, сделал одно открытие; после этого я быстро пошел вперед. Возникла гипотеза, что функция порядка 0 должна на достаточно больших окружностях иметь свойство

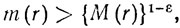
где m(r) и М(r) - максимум и минимум модуля. Доказательство этого, по крайней мере элементарными методами, достаточно трудно, и заняло у меня, вероятно, несколько месяцев. [Соответствующий результат для порядков, отличных от 0, состоит в том, что для порядков, меньших ¹/₂, m(r) так же велико, как некоторая положительная степень М (r) (на некоторых окружностях).] Это я мог доказать только для ¹/₄ вместо ¹/₂; полный результат был позже доказан А. Уайменом более "теоретико-функциональными" методами. Однако А. С. Безикович недавно возродил элементарные методы, которыми он доказал некоторые дальнейшие результаты. Я послал в Лондонское математическое общество длинную работу относительно функций порядка 0 (1 января 1907 г.). Теперь бы я ее написал значительно короче, но она была написана вполне прилично, и результат

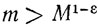
следует рассматривать как неплохой. Эта работа содержит также первое, насколько мне известно, применение метода усреднения. (Нужно доказать, что некоторая функция f(x) превышает определенное число m в какой-то точке отрезка 0≤x≤1. Так как ни о какой конкретной точке ничего нельзя сказать, то иногда представляется такой выход: показать, что среднее значение f(x) на (0, 1) превышает m; тогда должна существовать какая-то точка x, хотя мы и не можем указать ее, в которой f(x)>m.) Рецензенты разошлись во мнениях, причем один из них дал резко отрицательный отзыв (к тому времени, когда я узнал, кто был этим рецензентом, что произошло гораздо позже, я уже совершенно объективно считал его не очень умным). Харди был назначен третьим рецензентом, и работу напечатали. С тех пор у меня никогда не было никаких затруднений с публикацией работ, за исключением одной работа, написанной мной совместно с Харди, которая была отвергнута (совершенно напрасно) Кембриджским философским обществом.

Варнc счел возможным поставить теперь передо мной новую задачу: "доказать" гипотезу Римана. Это героическое начинание осталось все же небезрезультатным; мне придется начать с краткого очерка состояния теории ζ(s) и простых чисел в 1907 г. и, в частности, изложить, что я тогда по этому поводу знал. Я встретился с ζ(s) в книге Линделёфа, но в этой книге нет ничего относительно простых чисел, и я не имел ни малейшего представления о существовании какой-либо связи между этими вопросами; для меня г. Р. была просто знаменитой гипотезой из теории целых функций; все это произошло в Большие каникулы, когда я не имел доступа к литературе, к которой мог бы обратиться, если бы подозревал, что такая связь существует. (Даже среди лучше информированных людей только немногие слышали о работе Адамара, и еще меньшее число знало работу Валле-Пуссена в бельгийском журнале. Во всяком случае вопрос считался очень трудным и лежащим вне основного направления развития математики. Знаменитая работа Римана содержится в его собрании сочинений; в ней сформулирована г. Р. и приведено замечательное, но недоказанное "явное выражение" для π(x). Основная теорема теории простых чисел не упоминается, хотя ее содержание легко угадывается, если исходить из этого "явного выражения". В частности, Харди рассказал мне позднее, что он "знал" о том, что основная теорема теории простых чисел доказана, но думал, что это было сделано Риманом. Всё это сразу изменилось с появлением в 1909 г. книги Ландау.)

Я помнил формулу Эйлера

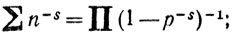
нас познакомили с ней в школе как с курьезным фактом (и поступили правильно, так как это прекрасная "шутка"). (Этой формулы нет в Алгебре Кристалла, что очень странно; но в главе о сходимости имеется пример с указанием: ∑f(p) сходится, если сходится 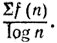Здесь опечатка: вместо n надо читать р. По поводу возникающего неверного утверждения я Сделал в 1902 г. пометку: положи f(p) = ¹/_p в 1902 г. я был уверен, что 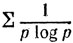сходится - это, ввиду формулы Эйлера, не так уж неправдоподобно.) В свете формулы Эйлера естественно изучать P(s) = ∑p^-s. Я вскоре обнаружил, что если основная теорема теории простых чисел верна с остаточным членом "порядка √x", то отсюда следует г. Р. Надо учесть, что в те времена никто из математиков, специально не знакомившихся с соответствующей литературой, не подозревал о существовании какой-либо чертовщины в распределении простых; поэтому ошибка в √х представлялась совершенно естественной по той причине, что простой делитель n не может превосходить √n. В силу всего этого я приступил к работе с большим воодушевлением и уверенностью в успехе, и только после недельных мучений осознал действительное положение вещей. Однако я заработал все же утешительный приз. Мне пришло в голову обратить рассуждение: я принял (по линии наименьшего сопротивления), что г. Р. действует для целой функции

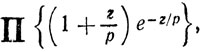
и отсюда успешно вывел основную теорему теории простых чисел. Это я тут же использовал в своей первой работе на соискание звания члена колледжа (сентябрь 1907 г.); в следующем году я забрал ее обратно.

Я ясно помню мои юношеские взгляды на основную теорему теории простых чисел, и они хорошо иллюстрируют шаткость суждений и вкусов начинающего математика в областях, где нет общепризнанных ориентиров. Мне самому очень нравились эти вещи; но я никоим образом не был уверен в том, как их воспримут другие, и если бы кто-нибудь сказал "неплохо, но все же уж очень специальный вопрос", "не настоящая математика", я бы покорно согласился. Харди (в то время младший член жюри) позже рассказал мне, что он "смело" выступал с заявлением, характеризующим эту часть работы как лучшую, не зная при этом, что результат был новым. Хотя в целом эта работа была принята благожелательно, я не был избран в пользу крайне нуждавшегося соискателя; однако было заключено джентльменское соглашение о том, что в следующий раз буду избран я.

С октября 1907"г. до июня 1910 г. я был лектором Манчестерского университета. Оклад в 250 фунтов стерлингов был, конечно, лучше, чем обычные 150 и 120 фунтов, и я последовал совету принять это предложение, что оказалось большой ошибкой. Я мог остаться в Кембридже как аспирант, и мне даже предложили одну из стипендий (которую, кстати, можно было получать наряду с окладом члена колледжа, если соискатель является таковым), но я отказался из-за работы в Манчестере. В смысле денег я ничего не выигрывал, но я чувствовал необходимость в перемене места и обстановки. Если моим дополнительным мотивом было желание много работать, то это желание исполнилось. Моя работа заключалась в следующем: 3 часа лекций провалившимся на вступительных экзаменах (университет за это получал деньги); 3 часа лекций студентам; 3 (иногда 2) часа лекции об основаниях математики учителям (в порядке "повышения квалификации" - совершенно бесполезная, естественно, затея); 2 часа практических занятий с сильными студентами 3-го года обучения, и 3 часа лекций для них же. Кроме этого, много свободного времени уходило на проверку письменных работ студентов младших курсов. В итоге получалось 4 часа работы утром по понедельникам, средам и пятницам, 3 часа утром по вторникам и четвергам; после обеда проверка работ и подготовка к лекциям в рабочей комнате университета примерно от 2.30 до 4 или 4.30. (Мы научились, конечно, читать элементарные лекции с минимумом подготовки, а иногда и просто экспромтом.) Суббота была свободным днем. Но если для большинства преподавателей рабочий день кончался в 4.30, то мне, сверх исполнения обычных обязанностей, приходилось вести еще сложную дополнительную работу. В то время сильные студенты третьего года обучения получали самое широкое математическое образование в стране. Несмотря на официальные экзамены, на которых предъявлялись нормальные для того времени требования, мы основательно изучали с ними в факультативном порядке разные избранные вопросы и занимались на практических занятиях полезными прикладными вещами. Мне была поручена та часть этой работы, которая относилась к чистой математике, причем я имел полную свободу выбора. В качестве одного из факультативных предметов я избрал дифференциальную геометрию. Этот предмет не доставлял мне больших забот, так как я рабски следовал своему конспекту лекций Германа, производя при этом необходимое рассредоточение материала. (Много лет спустя я рассказал об этом Харди, который в свою очередь сознался, что делал то же самое, когда в начале своей деятельности в качестве профессора геометрии^* Оксфордского университета узнал, что занимающий эту должность действительно обязан читать лекции по геометрии.) В остальном мои лекционные курсы относились к анализу. Эти лекции требовали от меня очень большой подготовки, которой мне приходилось заниматься по вечерам, причем должен сказать, что ни один курс из читанных мною впоследствии не отнимал у меня большего времени на подготовку. В течение первого года моей работы я не располагал вышедшими позже книгами Харди Курс чистой математики и Бромвича Бесконечные ряды; Жордан, по-видимому, не удовлетворял моих запросов; я мог бы до некоторой степени использовать Курс Гурса, но, как это ни удивительно, я не знал о его существовании. Сейчас уже нельзя представить себе тех трудностей, с которыми приходилось встречаться при составлении строгого формально-логического плана изложения, в котором не возникали бы неожиданные провалы (с этой стороны достижение Бромвича вызывало мое восхищение). Моей целью было научить математической технике бег претензий на изящество, но зато со всей строгостью (а мы рассматривали и такие вещи, как кратные несобственные интегралы), и это оказалось чрезвычайно трудным делом. Мои лекции пользовались некоторым успехом; временно они даже соблазнили Сиднея Чепмена стать аналитиком. (Мои затруднения еще усугублялись тем, что я был одним из самых безалаберных молодых людей; планы моих лекций были небрежно нацарапаны, что еще не составляет большой беды, но я писал их на отдельных разрозненных листах и содержал в столь хаотическом беспорядке, что их использование было невозможным уже в следующем году.) Ко всему этому остается только добавить, что 2 длинных триместра имели продолжительность в 10 педель каждый; единственное облегчение состояло в том, что Большие каникулы начинались рано, в июне. Такая напряженная работа рассматривалась как нормальное явление, если не считать моих специфических затруднений: что касается научно-исследовательской работы, то предполагалось, что она проводится в свободное время: я припоминаю одни пасхальные каникулы, когда я был так измотан" что не мог заставить себя работать, испытывая в то же время постоянные угрызения совести по поводу своего безделья. "Современная молодежь не знает, что такое работа". Добавлю еще, что Г. Ламб (занимая одновременно две должности профессора: чистой и прикладной математики) полностью выполнял свои двойные обязанности и находил еще при этом возможность уделять мне много внимания.

^* (По старинному обычаю в Англии (как и во Франции) словом "геометрия" часто обозначали всю математику в целом.- Примеч. пер.)

Я вернулся в Тринити-колледж в октябре 1910 г. (на место, которое занимал Уайтхэд). Этот момент совпал с возникновением новых математических интересов. Книга Ландау по аналитической теории чисел читалась с исключительным интересом; она навела меня на некоторые мысли о ζ-функции, но здесь нет нужды говорить об этом подробнее. Я живо помню, однако, забавную для меня историю поисков доказательства "теоремы Абеля - Таубера" (если ∑a_nx→s при x→1 и a_n = O(¹/_n), то ∑a_n сходится к s). Это произошло в Байдфорде во время пасхальных каникул 1911 г. Задача была, несомненно, поставлена передо мною Харди, но я не знал, что он уже доказал (более слабую) "теорему Чезаро - Таубера". Это очень странно, так как он, без сомнения, мне об этом рассказал; не думаю, что это произошло в то время, когда я активно размышлял над проблемами из этой области. С другой стороны, я тогда старался неукоснительно следовать правилу начинающих разузнавать все, что было сделано до них по вопросам, близким к изучаемому; по-видимому, этот случай был исключением. Как бы то ни было, все указанные обстоятельства содействовали успеху. Доказательство основной теоремы базируется на двух не связанных между собой идеях, одна из которых состоит в связи между тремя (или большим числом) последовательных производных (если f = o(1) и f" = O(1), то f' = o(1)^*). Я начал с теоремы Чезаро - Таубера, и в процессе отыскания доказательства пришел к теореме о производных; если бы я знал доказательство теоремы Чезаро - Таубера, то теорема о производных, будучи просто одним из звеньев готового доказательства (кстати, весьма отличного от моего), не обратила бы на себя моего внимания, а без этого я никогда не доказал бы основной теоремы. (Теорема о производных была вообще уже известна, ко похоронена в недрах одной работы Адамара о волнах.) Начинать думать над проблемой, не вникая особенно глубоко в существующую литературу, является, конечно, правильным методом работы, и я его часто применяю.

^* (Увы, Дж. И. Литлвуда, хотя я ее переоткрыл, и это было важным моментом в моей карьере. Я упоминаю о ней потому, что я получил ее, используя графическое рассуждение.)

Теорема о производных позволяет отбрасывать некоторые части выражения, стремление к нулю которого нужно доказать. Однажды, когда я обдумывал с разных сторон это предложение, у меня смутно возникла мысль сделать число дифференцирований r большим. В этот момент до комнаты, где я работал, дошла очередь подвергнуться весенней уборке. Мне ничего не оставалось, как уйти на 2 часа гулять под проливным дождем. Проблема продолжала с силой бурлить в моей голове: рассуждения были обременены несущественными осложнениями, которые в окончательной редакции были устранены, а "идея" все еще была неопределенной и ускользающей. Наконец, я остановился под дождем на мосту (вблизи Кенвичского леса), глядя невидящим взглядом на поверхность реки; через несколько минут меня вдруг захлестнула уверенность, что теорема доказана. Все же 40 минут, которые прошли до моего возвращения и окончательной проверки, были чрезвычайно напряженными.

Оглядываясь назад, я вижу, что именно в это время мои математические вкусы приобрели устойчивость и я пришел к более или менее уверенному суждению о сравнительной ценности тех или иных математических открытий; это был конец моего "образования". Вскоре началось мое 35-летнее сотрудничество с Харди.