От последней теоремы Ферма до отмены смертной казни

(Основное содержание этой главы было изложено в моей лекции в Ливерпуле в 1929 г. П. Т. Ф. утверждает, что для целого n>2 уравнение xⁿ + yⁿ = zⁿ неразрешимо в целых числах x, y, z, отличных от 0. Достаточно решить вопрос в том случае, когда n есть простое р. Верна эта теорема или нет, до сих пор неизвестно.)

Теперь уже всеми признано, что чистая математика может привести к неожиданным выводам и даже оказать влияние на повседневную жизнь. Может ли существовать цепочка мыслей, приводящая к заглавию этого очерка? Я думаю, что да, хотя, конечно, с некоторыми натяжками; именно, я хочу представить себе одно или два правдоподобных изменения в ходе истории математики. Любителя следует, быть может, предупредить, что рассуждение будет вначале развиваться несколько медленно, но зато под конец оно будет двигаться очень быстро, я надеюсь, что при этих условиях читателя можно будет убедить следовать за нами в начале нашего пути (где мы будем, кстати, иметь дело с идеями большой математической значимости).

Теория чисел, более чем какая-либо другая математическая дисциплина, беззащитна перед упреком, что некоторые из ее проблем возникают в связи с вопросами, которых вообще не следовало бы ставить. Я лично не думаю, что опасность серьезна; в результате концентрированного обдумывания в течение разумного времени либо появляются новые интересные идеи и методы, либо проблему приходится попросту оставить. "Совершенные числа" заведомо никогда никакой пользы не принесли, но они и не причинили особого вреда. П. Т. Ф.- более серьезный случай, эта теорема имеет все внешние признаки "неправильного вопроса" (к тому же ее утверждение носит негативный характер); но работа над этой теоремой привела, как мы знаем, к важному математическому понятию "идеала". Это - первое звено в моей цепочке мыслей.

Интенсивное изучение П. Т. Ф. вскоре показало, что для более глубокого ее понимания необходимо обобщить эту теорему^*; числа х, y, z из "невозможного" равенства x^p + y^p = z^p были заменены целыми числами "поля" уравнения ζ^p + 1 = 0. Если α - корень (отличный от -1) этого уравнения, то под целыми числами поля понимают (в формулировке, достаточной для наших целей) все числа вида m₀+m₁α+. . .+m_p-2α^p-2, где m₀, m₁, ..., m_p-2 - "обыкновенные" целые числа (любого знака). Идея делимости целого числа а поля на другое целое число b поля достаточно проста; а делится на b, если а = bc, где с - целое число поля. Далее, простое число поля - это такое целое число поля, которое не имеет "собственных" делителей, т. е. которое делится только на самого себя и на "единицы" поля (обобщения "1", на них делятся все целые числа поля). Любое целое число (поля) может быть разложено на простые "множители". Но тут возникает новая ситуация в полях, соответствующих некоторым (фактически большинству) р, заключающаяся в том, что это разложение на простые множители не всегда однозначно (для обыкновенных целых чисел оно всегда однозначно). Для того чтобы восстановить единственность разложения^**, привлекаются "идеалы".

^* (И, следовательно, решать, по всей видимости, более трудную проблему!)

^** (Для целых чисел поля любого алгебраического уравнения a₀ + a₁ζ + ... +a_nζⁿ = 0, где a₀, a₁, ..., a_n - обыкновенные целые числа.)

Такие новые понятия, как идеалы, обычно вводятся сначала постулированием, и только позже ставятся на твердую почву конструированием объекта с требуемым поведением^*. Простейший путь для нас состоит в том, чтобы сразу дать построение Дедекинда и исходить из него. Пусть α, β, ..., א - любое конечное множество целых чисел поля; рассмотрим класс всех чисел (они - целые числа поля) вида mα + ... + k א, где m, ..., k - обыкновенные целые числа; каждое число класса считается только один раз (если имеются перекрытия). Класс, полностью определенный множеством α, ..., א, обозначается через (α, ..., א) и называется идеалом. Вернемся теперь к полю обыкновенных целых чисел и посмотрим, во что превратится идеал в этом частном случае. Обыкновенные

^* (Другие примеры: комплексные числа" бесконечно удаленные точки, неевклидова геометрия.)

целые числа α, ..., א имеют наибольший общий делитель d (этот факт в действительности является основой единственности разложения на простые множители, и Евклид строит свое доказательство, исходя именно из этого факта; поэтому доказательство Евклида является "правильным" доказательством, хотя в учебниках часто дается другое доказательство). Класс чисел mα + ... + k א без учета многочисленных перекрытий совпадает, как легко видеть, с классом чисел nd (n пробегает все обыкновенные целые числа); идеал (α, ..., א) тождествен идеалу (d). Идеал в произвольном поле, имеющий форму (α), где α - целое число поля, называется главным идеалом; поле, в котором целыми числами являются только обыкновенные целые числа, обладает, таким образом, тем свойством, что все его идеалы - главные. Предположим теперь, что а, b - обыкновенные целые числа и что а делится на b, например, пусть а = 6, b = 3. Тогда (а) является классом всех чисел, кратных 6, (b) - классом всех чисел, кратных 3, и класс (а) содержится в классе (b). Обратно, класс (а) может содержаться в классе (b) только в том случае, когда а делится на b. Следовательно, утверждения "a делится на b" и "(а) содержится в (b)" эквивалентны. Но множество элементов (а) находится в точном соответствии с множеством элементов а (без скобок); в качестве исходного материала мы можем взять вместо целых чисел а идеалы (а), и под "b является делителем а" понимать "(а) содержится в (b)". Теория заключенных в скобки элементов развивается совершенно параллельно теории элементов, не заключенных в скобки, и является простым "переводом" последней. Вернемся теперь к общему полю. Целое число а заменяется на (α), но уже не все идеалы являются главными; в качестве исходного материала берутся все идеалы, и делимость одного идеала на другой (понятие, пока не определенное) понимается как включение первого из них (как класса) во второй. Предположим теперь, обозначая идеалы жирным шрифтом, что α, ..., k - конечное множество идеалов. Тогда существует идеал d, который включает в себя α, ..., k и является наименьшим идеалом с этим свойством^*; d играет роль "наибольшего общего делителя" α, ..., k. После этого мы без труда (и вполне аналогично случаю обыкновенных целых чисел) Приходим к основному предложению об однозначной разложимости каждого идеала в произведение "простых идеалов". Так как эта теория "приводится" к "обыкновенной" теории в частном случае "обыкновенных" целых чисел, она является, подлинным обобщением этой последней, и про нее можно с полным основанием сказать, что она "восстанавливает" однозначность разложения на множители.

^* (Если α = (α₁, β₁, ..., א₁), ..., k = (α_n, β_n, ..., א_n), то d = (α₁, ..., א₁, α_n, ..., א_n).)

Я не могу избавиться от чувства, что сначала "следовало" создать идеалы и, отправляясь от них, прийти к знаменитому определению "действительных чисел" сечениями Дедекинда. Хотя такая возможность была близка к осуществлению, действительный ход событий был иным^*. Мы предположим, однако, историю несколько измененной.

^* (Публикация была более или менее одновременной (и более поздняя идея уже имелась для ревизии более ранней), но идея "сечения", опубликованная в 1872 г. (Was sind und was sollen die Zah-len?), зародилась в 1858 г.)

В определении дедекиндова сечения все рациональные числа распределяются на два класса, L и R^*, причем каждое число из L расположено левее (т. е. оно меньше) каждого числа из R (и, для определенности, L не содержит наибольшего числа, тогда как R может содержать наименьшее число, но может и не содержать его). Совокупность всевозможных сечений в множестве рациональных чисел представляет собой множество элементов, обладающих теми свойствами, которые мы хотели бы придать континууму "действительных чисел", и последние становятся надлежащим образом обоснованными.

^* (Обозначения L и R (left - левый, right - правый.- Примеч. пер.), которые с благодарностью восприняло целое поколение студентов, были введены мною. В первом издании Pure Mathematics (Харди Г. Курс чистой математики.- Примеч. пер.) классы обозначались через Т и U. Более поздние издания содержат много ссылок на меня, но, когда я намекнул Харди, что ему следовало бы отметить и эту мою заслугу (что не было сделано), он отказался выполнить мою просьбу на том основании, что упоминать такие мелочи было бы оскорбительно для меня. (Это известная отговорка угнетателей: то, чего жертва хочет, не служит ее истинным интересам.))

Что же, по существу, означает "сечение" (Schnitt)? После определения идеала как класса представляется естественным (и даже неизбежным) определить действительное число как класс L (можно было бы, конечно, определить его и как класс R). Так, действительное число √2 есть класс рациональных чисел r, составленный из всех отрицательных рациональных чисел и тех неотрицательных рациональных чисел, для которых r²>2. Разумно считать этот шаг сделанным и под определением Дедекинда понимать определение через классы. Фактические обстоятельства были довольно странными. Для самого Дедекинда Schnitt был актом разрезания, а не тем, что отрезалось, он "постулирует", что "действительное число" осуществляет разрезание, но не может с этим полностью примириться (современный студент легко примиряется с классом). Как говорит Бертран Рассел, метод постулиро вания имеет много преимуществ, совпадающих с теми, которые присущи воровству по сравнению с честным трудом. Между прочим, с чисто лингвистической точки зрения слова Schnitt и Section означают и акт разрезания, и то, что оказывается отрезанным. Это тот случай, когда невер-ное лингвистическое толкование могло бы означать научный прогресс.

Определения через понятие класса, подобные рассмотренным (идеал и действительное число), не встречались в науке с 350 г. до н. э. Евдоксово определение (пятая книга Евклида) равных отношений (несоизмеримых величин) очень близко к сечению Дедекинда (евдоксовы равные а:b и c:d соответствуют каждое одному и тому же классу рациональных чисел m/n эти два отношения должны считаться равными, если класс m/n, для которых ma<nb, совпадает с классом m/n, для которых mc<nd).

Обратимся теперь к другому вопросу: что понимается под "функцией"? Я отвлекусь (имея в виду определенную цель) и приведу в интересах начинающего некоторые цитаты из книги Форсайта Теория функций комплексной переменной^*. (Книга Форсайта была устаревшей уже в 1893 г., когда она только писалась, но моему поколению приходилось часто встречаться с таким положением.) Тот факт, что регулярность функции комплексной переменной объясняется тут же, только усугубляет общий кошмар, но мне не хотелось бы лишать читателя известного интеллектуального наслаждения. Если читатель почувствует, что он дальше читать не в состоянии, то пусть знает, что цитата кончается на с. 67, строка 5.

^* (Forsуth A. R. Theory of Functions of a Complex Variable.)

"Все обыкновенные операции, будучи произведены над комплексными переменными, приводят, как уже отмечалось, вновь к комплексным переменным; и всякое определенное количество, полученное таким образом при помощи операций над z, необходимо является функцией z.

Но если комплексная переменная w дана как комплексная функция х и y без каких бы то ни было указаний на ее происхождение, то вопрос о том, является w функцией z или нет, требует рассмотрения общей идеи функциональности.

Удобно постулировать u + iv как форму комплексной переменной, где u и v вещественны. Так как w априори не ограничено в своем изменении, мы можем рассматривать величины u и v как независимые и, следовательно, как произвольные функции x и y - элементов, входящих в z. Но более явные выражения для этих функций не будут приводиться, и существование таких выражений не предполагается.

Возникновение идеи функциональности вначале было связано с функциями вещественных переменных, и тогда эта идея была равнозначна идее зависимости. Так, если значение X зависит от значения хине зависит ни от какой другой изменяющейся величины, то принято X рассматривать как функцию х; при этом обычно еще подразумевается, что X выводится из х при помощи ряда операций.

Детальное знание z однозначно определяет x и y; поэтому значения u и v могут рассматриваться как известные, а следовательно, известным будет также и w. Таким образом, значение w зависит от значения z и не зависит от значений переменных, не связанных с z; имея в виду упомянутое выше понятие функциональности, мы можем теперь сказать, что w является функцией z.

Вполне совместным с рассмотренной точкой зрения будет, однако, и понимание комплексной функции как функции двух независимых элементов, из которых составлено z; и мы приходим всего лишь к рассмотрению функций двух вещественных независимых переменных с (возможно) мнимыми коэффициентами.

Оба эти аспекта зависимости w от z предполагают, что z рассматривается как составная величина, содержащая два независимых элемента, которые могут быть отделены друг от друга. Нашей целью, однако, является понимание z как наиболее общей формы алгебраической переменной, которая является неразлагаемым целым. Поскольку это предварительное условие по отношению к z оказывается невыполненным, ни один из указанных аспектов не может быть нами принят.

Допустим, что w понимается как функция z в том смысле, что она может быть построена при помощи определенных операций над z, рассматриваемым как неразлагаемая величина, и что и и v возникают после выполнения всех бтих операций отделением действительной и мнимой части при замене z на x + iy. Таким образом, предполагается, что одной серии операций достаточно для одновременного построения и u, и v, в отличие от общего случая построения комплексной функции (см. выше), где требовалась одна серия операций для и и другая для v. Бели это предположение оправдывается тем, что эти два различных метода построения приводят к одной и той же форме функции, то отсюда вытекает, что обе серии операций, которые приводят в общем случае к u и v, должны быть эквивалентны той единственной серии, которая приводит сразу и к u, и к v, т. е. что между этими величинами должны существовать какие-то соотношения; другими словами, u и v, как функции от x и y, должны иметь родственные функциональные формы:

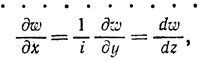
(1)

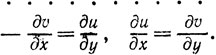
(2)

Это - необходимые... и достаточные... соотношения между функциональными формами u и v.

Приведенное выше определение необходимых и достаточных условий функциональной зависимости основывается на существовании функциональной формы, но в то же время сама эта форма оказывается несущественной, ибо как мы это уже отмечали, она исчезает из формулировки условий. Постулирование существования такой формы эквивалентно предположению, что значение функции может быть вычислено для каждого конкретного значения независимой переменной, хотя явная формулировка этой предпосылки в данном случае исчезла из нашего поля зрения. Обращение с функциями действительных переменных показывает, что в большинстве случаев удобнее использовать их свойства, чем знать их частные числовые значения. Это подтверждается также сказанным выше. Существенными условиями функциональной зависимости являются уравнения (1)...".

В наше время, конечно, функция y = y(х) означает, что имеется класс "аргументов" x и что каждому x поставлено в соответствие одно и только одно "значение" y. После некоторых тривиальных разъяснений (а может быть, и без них?) мы можем осмелиться сказать, что функция есть просто класс С пар (x, y) (с учетом порядка в скобках), подчиненный (только) тому условию, что х в различных парах должны быть различными. (И утверждение "между x и y есть зависимость R" означает просто задание класса, который может быть любым классом упорядоченных пар.) В наше время, кроме того, х может обозначать элемент любой природы так же, как и y (например, класс или высказывание). Если мы хотим рассматривать функции, которые себя "хорошо ведут", например непрерывные функции действительной переменной, или f(z) Форсайта, то мы определяем, какая функция называется непрерывной и т. д. (на что для функции Форсайта понадобятся 2 строки), и рассматриваем класс таких функций. Вот и все. Такая ясность дневного света считается теперь само собой разумеющейся, но она сменила мрак полуночи^*. Основной шаг был сделан Дирихле в 1837 г.^** (для функций действительной переменной, где класс аргументов состоит из некоторых или всех действительных чисел, и класс значений также ограничен действительными числами). Для функций высказываний, например, полное равноправие было достигнуто в 1920-х годах.

^* (Несчастье состояло, конечно, в навязчивой мысли, что значение функции "должно" получаться из аргумента при помощи "серии операций".)

^** (И Лобачевским, сделавшим его еще раньше.- Примеч. пер.)

Предположим теперь, вновь представляя себе историю несколько иной, чем она была на самом деле, что внесение ясности произошло позже, и было связано (как это легко могло случиться) с успехом идей Дедекинда. Я буду, следовательно, считать, что идея функции возникла в связи с теоремой Ферма. (Если это отклоняется, то "отмена смертной казни" вместо теоремы Ферма должна быть связана с рядами Фурье или дифференциальным уравнением теплопроводности.)

Рассмотрим теперь функцию, для которой класс аргументов состоит из моментов t (исторического) времени, а значение f(t) является состоянием Вселенной (описываемым достаточно подробно с учетом всех событий, которые могут кого-либо интересовать). Если t₀ - настоящий момент, то f(t) для t<t₀ представляет собой описание или словарь всего того, что произошло. Предположим теперь, что этот словарь перенесен назад, т. е. отнесен к более раннему моменту времени τ; тогда он содержит предсказания о том, что должно случиться между моментами τ и t₀. Ясно, что это рассуждение имеет прямое отношение к проблеме о детерминизме и свободе воли и может повлиять на колеблющихся. Колебания в вопросе о свободе воли отражаются на решении проблемы моральной ответственности и, таким образом (хорошо это или плохо), на решении проблемы наказания. Некоторые реформаторы руководствовались и более дикими идеями.