Баллистика

16."Задача стрелка". Следует ли при данном расстоянии до цели увеличивать или уменьшать угол подъема φ (отсчитываемый от направления в цель), если цель находится несколько выше горизонтали? Ответ, вероятно, не очевиден, он интуитивно ясен, если цель находится ниже горизонтали, и поэтому скорость возрастания φ в зависимости от угла α наклона направления в цель к горизонтали нужно считать положительной, так что ответ на основной вопрос должен состоять в увеличении φ. Для средних расстояний φ стремится к нулю, когда α стремится к ^π/₂, так что начальное увеличение φ затем переходит в уменьшение. В результате можно предполагать, что разумно хорошим приближением будет постоянное φ, если α достаточно мало и положительно^*; это называется "принципом жесткости траектории".

^* (Это приближение улучшается, если принять во внимание уменьшение плотности воздуха с высотой. Соответствующие вычисления легко проводятся для траекторий в пустоте; относительное Поведение фактических траекторий почти такое же (и во всяком случае стремится к поведению в пустоте при φ→0).)

Стрелок-профессионал считает, что φ надо увеличивать, если цель находится над горизонталью; он прав, так как поправка, которая в конечном счете приводит к уменьшению φ, вблизи горизонтали имеет второй порядок малости.

В пустоте высота траектории с целью на горизонтали

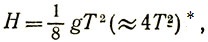
где Т - время полета. Это оказывается очень хорошим приближением для всякого рода орудий и всех углов подъема (даже для вертикальных траекторий).

^* (Если за единицу длины принять английский фут.- Примеч. пер.)

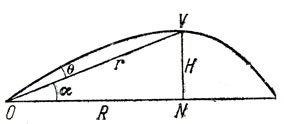
Рис. 16

Примем эти два принципа, считая их точными, а не приближенными. Тогда становится возможным найти положение вершины траектории при помощи следующего остроумного рассуждения, использующего только артиллерийские таблицы. *Артиллерийская таблица дает любые две из величин: R (дальность), φ (угол подъема), Т (время полета, а вместе с ним и Н = 4Т²) как функции третьей. На рис. 16 мы имеем для данного φ

откуда

и корень θ(φ) может быть приближенно найден методом проб, а с ним α и ON.*

Я столкнулся с этим вопросом при следующих обстоятельствах. Однажды вечером, незадолго до того, как я начал работать в Артиллерийском управлении (примерно в декабре 1915 г.), я был дежурным офицером по большому полигону, где было много старших офицеров (не являвшихся, однако, специалистами в области баллистики). На столе

в комнате дежурного лежал лист бумаги с чертежом рис. 16 и всеми обозначениями, из которых легко можно было усмотреть, о чем идет речь. Через день или два после этого меня вызвал полковник и спросил, не знаю ли я способ нахождения вершины V. Со всей серьезностью я изложил ему приведенное выше рассуждение, а так как оно было, по-видимому, новым для него, то мне показалось забавным ничего к этому не добавлять. (Я так никогда и не узнал, откуда взялся этот чертеж.)

17.Ракеты. Траектория частицы под действием земного притяжения и постоянной силы - старая игрушка динамики точки. Теоретически траектория не может начинаться из положения покоя иначе, как вертикально (при вертикальном старте начальная кривизна бесконечна).

Какие кривые имеют: а) изящную форму, б) изящное уравнение? Траектория бомбы имеет приближенное уравнение

Я слышал рассказ одного офицера о битве у Фольклендских островов {в 1914 г., в начале войны), в которой он принимал участие. Немецкие корабли были уничтожены с максимального расстояния, но на это потребовалось много времени, и залпы постоянно ложились на 100 ярдов левее. Эффект вращения Земли, аналогичный "дрейфу", учитывался наводящим устройством. Но это устройство было рассчитано на то, что морские битвы будут иметь место в районах широт 50° N. Двойная поправка для 50° S и максимального расстояния имеет порядок 100 ярдов.

*18. Допустим, что материальная точка падает вертикально вниз в среде, плотность ρ которой возрастает с глубиной y как 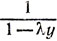и сопротивление которой изменяется как ρν², так что отрицательное ускорение от сопротивления среды по абсолютной величине равно 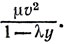Если μ = λ, то независимо от начальной скорости движение оказывается гармоническим (пока оно вообще происходит; наинизшая точка траектории совпадает с тем местом, где плотность становится бесконечной). Мои неоднократные попытки включить этот вопрос в экзаменационные билеты всегда отклонялись. Я надеялся услышать критику по линии "нереальности" задачи, на что существует следующий ответ. В 1917-1918 гг. потребовалось составить впервые, и притом быстро, артиллерийскую таблицу для самолетной пушки, стреляющей на данной высоте в любом направлении. Существовал метод вычисления, основанный на использовании данных для вертикальных траекторий, направленных вверх и вниз. Оказалось, что значения μ и λ можно было считать с достаточной точностью равными (и ρ = (1-λy)^-1 также было достаточно точной аппроксимацией закона плотности). Вертикальная траектория, направленная вниз, могла быть, следовательно, просто считана с таблицы синусов, и артиллерийская таблица была фактически составлена именно таким образом (примерно в ²/₃ того времени, которое на нее понадобилось бы при ином способе составления).

19. Я не отрицаю, что только что приведенный пример не представляет большого интереса; вот более интересный пример. Для любого "свойства" траектории в атмосфере переменной плотности, скажем, для свойства иметь данное R для данного угла подъема φ (и фиксированного "оружия"^*), существует "эквивалентная однородная атмосфера" (для которой R при данном φ то же, что и в реальной атмосфере; эквивалентная атмосфера меняется с φ); она характеризуется числом с<1 таким, что эквивалентная постоянная плотность равна фактической плотности на высоте ch, где h - наибольшая высота траектории. Оказывается, что во всякой такой задаче в пределе, когда R→0, с является постоянным числом, не зависящим от закона сопротивления и характера изменения плотности. В частности, для свойства иметь данное R предельное значение с равно ³/₅. (Это предельное значение зависит от задачи, и, например, для свойства иметь данное время полета при данном φ равно ²/₅. Вывод этих результатов из основных принципов требует довольно сложных вычислений, которые, однако, могут быть несколько упрощены, если принять заранее, что предел будет постоянным.) Так как "средняя высота" в любом обычном смысле этого слова равна ²/₃ h, сформулированные результаты являются довольно тонкими (в Артиллерийском управлении не хотели всему этому верить, пока не был произведен эксперимент; после этого они верили любому результату, предсказанному теорией).

^* ("Орудие" - это упорядоченная пара констант (с, V))

Если что-либо можно считать интуитивно ясным, так это то, что с ни для какого "свойства" не может лежать вне интервала (0,1); как читатель относится к возможности с = 0 или 1?

Фактически существует очень простой (и практически важный) случай, для которого с = 0: это задача "время полета на данной наклонной плоскости при заданном угле подъема".

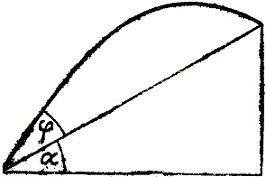
Рис. 17

Так как высота h здесь первого порядка малости^* (для траектории с горизонтальной Землей она второго порядка), вычисления становятся более простыми. Если мы используем тот факт, что с не зависит от закона сопротивления и характера изменения плотности (парадокс, во всяком случае, не менее ярок в этом предельном случае), мы можем упростить задачу следующим образом. Нормируя притяжение Земли и начальную скорость к 1, мы можем предположить, что "ускорение" будет иметь вид -μ(1-λy)v, где y мало. Пусть φ - угол подъема, α - угол наклонной плотности с горизонтом (рис. 17). Реальная траектория является решением системы

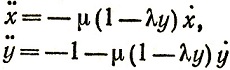
с начальными значениями 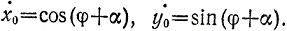Время τ, при котором y = х tg α, должно быть приравнено соответствующему времени с заменой λ на 0 и μ на μ'= (1-ch)μ. Если мы перейдем к пределу при φ (или τ) и μ, стремящихся к 0 (λ→ 0 не обязательно), то это будет, между прочим, означать, что всеми членами, содержащими μ², можно пренебречь. Тогда приближенно

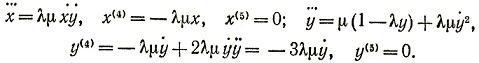
^* (Как функция от R при R→0.- Примеч. пер.)

В момент τ мы имеем, полагая γ = cos (φ + α), σ = sin (φ + α),

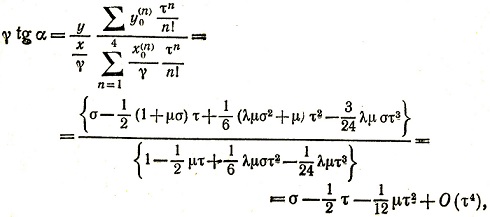
что находится прямым вычислением с пренебрежением μ²; заметим, что член с τ³ отсутствует.

Правая часть должна быть равна

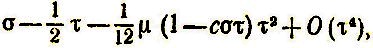
а отсюда с = O(τ) и предел с = 0.*