Зоопарк

15. Область, получающаяся из круга выбрасыванием бесконечного множества таких секторов, как заштрихованные на рис. 10, имеет важные приложения в теории функций (слишком сложные для разъяснения здесь). Она обычно называется амебой или морской звездой.

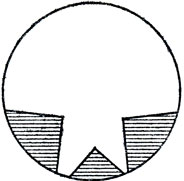
Рис. 10

Змея. Функция f(z), отображающая область, изображенную на рис. 11, на единичный круг, принимает некоторые значения дважды (те, которые принадлежат дважды покрываемой части), но f' нигде не обращается в нуль. (Ошибочное представление, что f' должно обращаться b нуль, чрезвычайно распространено, несомненно в результате диеты, слишком богатой алгебраической теорией функции, в которой все листы римановых поверхностей идентичны и располагаются над всей плоскостью.)

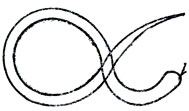
Рис. 11

Крокодил (рис. 12). Зубы заходят один за другой и имеют бесконечную общую длину. Если эту область отобразить на единичный круг, то мы получим пример функции f(z)= ∑c_nzⁿ, вещественная часть которой U(θ) = Re f(e^iθ) имеет ограниченное изменение, а мнимая часть V(θ) как угодно близка к этому. С другой стороны,

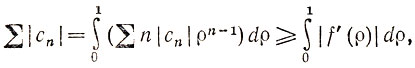
а последний интеграл представляет длину образа радиуса (0,1) круга в z-плоскости. Этот образ, однако, является линией, извивающейся между зубами к носу, и имеет бесконечную длину. Поэтому ряд ∑|c_n| расходится.

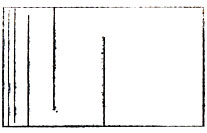
Рис. 13

Известно, что если U и V имеют ограниченное изменение, то этот ряд сходится. Крокодил показывает, что этот результат является наилучшим возможным - ответ на когда-то заданный мне (проф. Л. С. Янгом) вопрос. Однажды, когда я возвращался с пешеходной прогулки в Кембридж, думая над этим вопросом, мне пришел в голову - неизвестно откуда - "гиппопотам" (рис. 13,- хорошо известный персонаж^* из теории "простых концов", но только теперь я решился окрестить его так, в подражание крокодилу). Он не совсем давал решение вопроса (или мне так показалось) и через несколько сотен ярдов превратился в крокодила.

^* (Настолько хорошо известный, что мой художник не решился его нарисовать.)

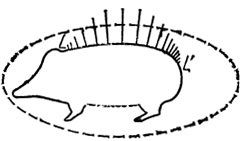
Рис. 14

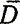Дикобраз. Допустим, что топологическое преобразование Т таково, что ТⁿР для каждой точки Р плоскости в конце концов (т. е. для n>n₀(Р)) попадет в ограниченную область Δ и останется там. Пусть Δ₊ - немного увеличенное Δ (такое, что замыкание области Δ содержится в Δ₊). Пусть - любая замкнутая ограниченная область. Верно ли, что ТⁿР сходится равномерно в Δ₊ для всех Р из 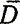(т. е. Tⁿ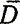⊂Δ₊ для n>n₀(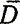))? Каждый сначала подумает, что это действительно так (для одномерного аналога это даже верно), однако ответ оказывается отрицательным. Это доказывает пример (рис. 14), найденный мисс Картрайт и мной (на спине у дикобраза бесконечное множество игл с предельными точками L и L'). Рассмотрим T, которое оставляет дикобраза - фигуру, очерченную сплошной линией,- инвариантным в целом, но переводит каждую иглу в следующую за ней справа, и, кроме того, приближает все внешние точки к контуру дикобраза. А - область, ограниченная пунктирной линией, Δ₊ - сколь угодно мало увеличенное Δ. Тогда ТⁿР в конце концов попадает внутрь Δ для каждого P, но для конца иглы вблизи L требуется большое n, для того чтобы ТⁿР в конце концов попало в Δ₊.

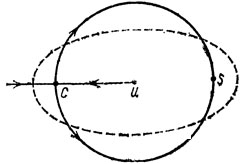
Рис. 15

Позже мы нашли значительно более простой пример (рис. 15), в котором u, s, с - соответственно вполне нестабильная, стабильная и метастабильная фиксированные точки Т, и линии фигуры инвариантны в целом относительно T. Δ - область, ограниченная пунктирной линией. Каково бы ни стало Р, ТⁿР в конце концов остается в Δ, но точки вблизи u, а также точки, лежащие вблизи линии uс, попадают в Δ₊ как угодно поздно. Это T, однако, оставляет всю площадь инвариантной, и этот пример не покрывает важного класса преобразований T, при итерировании которых площадь каждой ограниченной фигуры стремится к нулю. Дикобраз может сделать и это, если свести к нулю площадь его тела; при этом он не исчезает, а из него только выпускают воздух.*