
Недоразумения, неосознанные предпосылки, вопиющие ошибки, опечатки и т. п.
11. Я однажды возражал против неправильного употребления моим учеником фразы "предположим для простоты". Она должна означать, что автор может сделать то, что требуется и без упрощения, но щадит читателя; оказалось же, что мой ученик должен был упростить задачу, чтобы он сам мог ее решить.
Конечно, почти невозможно полностью избежать неосознанных предпосылок. Я помню одно место из книги Ламба Higher Mechanics: "Ох и Оy как в двух измерениях, Oz вертикальна". Для меня это совершенно неверно; Oz горизонтальна (я работаю всегда, откинувшись в кресле и подняв ноги).
Как читатель изобразил бы замкнутую кривую (например, окружность), лежащую целиком по одну сторону от одной из своих касательных? Существует 4 школы; я принадлежу к той, для которой кривая лежит справа от вертикальной касательной; однажды мне пришлось описывать эту конфигурацию без чертежа, но то, что я говорил, оказалось непонятным для представителей 3 остальных школ.
Как не надо. Один блестящий, но небрежный математик однажды сформулировал теорему в двух частях и добавил: "часть 2, принадлежащая Харди и Литлвуду, тривиальна". Тривиальная часть 2 должна была фигурировать в формулировке "для полноты", Харди и Литлвуд включили ее по этой же причине. Автор чересчур скрупулезно старался не нарушить правила, согласно которому ничего из уже опубликованного не должно приводиться без соответствующей ссылки.
При изложении математического рассуждения мастерство заключается в умении дать образованному читателю возможность сразу, не заботясь о деталях, схватить основную идею; последовательные дозы должны быть такими, чтобы их можно было глотать "с ходу"; в случае неудачи, или если бы читатель захотел что-либо проверить, перед ним должна стоять четко ограниченная маленькая задача (например, проверить тождество; две пропущенные тривиальности могут в совокупности образовать непреодолимое препятствие). Неопытный автор не предоставляет своему читателю такой возможности; даже если у читателя и возникает первое смутное представление" он не успевает осознать существа дела, пробираясь через лес символов, в котором даже самый мелкий индекс не может быть опущен. Ниже я привожу пример (из анализа, где встречаются наибольшие трудности). Этот пример далеко не экстремальный, он может встретиться в любой рукописи до того, как ее просмотрит какой-либо заслуживающий сочувствия редактор. Кроме того, этот пример обрисовывает преступление в слишком мягком свете, так как основную идею доказательства здесь очень трудно затушевать. Но не так-то легко заинтересовать читателя скучным текстом, и за отсутствием в настоящий момент образца натурального продукта, это - лучшее, что я могу предложить.
*Знаменитая теорема Вейерштрасса утверждает, что любая непрерывная в прямоугольнике R функция f (x1, х2) может быть равномерно приближена последовательностью многочленов от x1 и х2. Теорема справедлива и в n измерениях; начинающий автор даст приведенное ниже доказательство, и к тому же еще в n измерениях, вводя обозначения x1, х2, ..., хn; х1', х2', ..., хn'. Доказательство является смелой комбинацией идей, и состоит из двух частей; вторая часть не может быть сильно испорчена, и я даю ее в конце. Вот изложение первой части доказательства начинающим автором. Несколькими удачными ухудшениями я обязан д-ру Флетту. Для дополнительного реализма я оставляю неисправленными несколько случайных опечаток.
Пусть с>0, и функция f1(x1, х2), непрерывная в прямоугольнике (-a≤x1≤a, -b≤x2≤b), определена следующим образом:
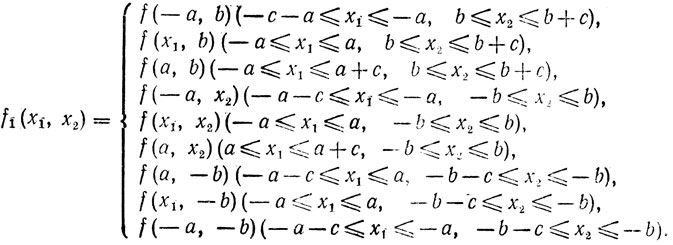
Легко видеть, что f1(x1, х2) непрерывна в прямоугольнике
(-a-c≤x1≤a+c, -b-c≤x2≤b+c)
Для точек (x1, х2) из R положим
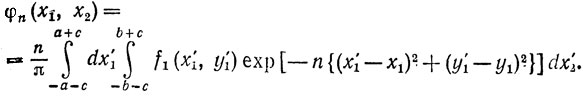
Покажем [это и будет первой частью доказательства], что
φn(x1, x2) → f(x1, x2) при n→∞(1)
равномерно относительно (x1, х2) из R.
Существует δ(ε) такое, что
|f1(x1", x2") - f1(x1', x2')|<ε
при условии, что (x1', x2') и (x1", x2:) принадлежат прямоугольнику
(-a-c≤x1'≤a+c, -b-c≤x2'≤b+c)
и удовлетворяют неравенствам
|x1"-x1'|<δ(ε)
и
|x2"-x2'|<δ(ε).
Пусть
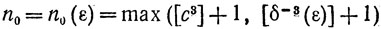
и n>n0. Тогда
-a - c<x1-n-1/3<x1+n-1/3<a+c,
-b - c<x2-n-1/3<x2+n-1/3<b+c,
и мы имеем
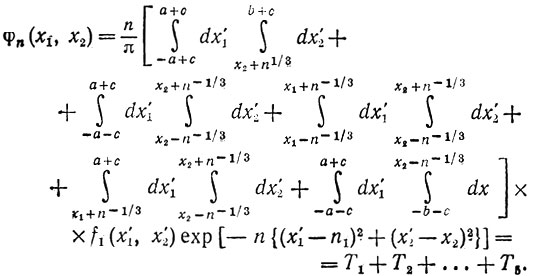
В T1 мы имеем
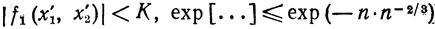
(2)
и, следовательно,
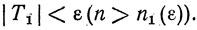
(3)
Аналогично*
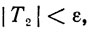


(4)
* (Открою в этом месте, что в Т2 есть опечатка:
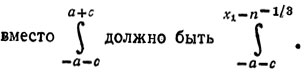
Математический текст такого стиля (вдохновленный, несомненно, дьяволом) не может не содержать опечаток.)
В Т3 положим x1' = x1 + x1", x2' = x2 + x2". Так как |x1"|≤n-1/3, |x2"|<n-1/3, то в рассматриваемом интервале мы имеем

(5)
Но в Т3 f(x1, x2) = f1(x1, x2). Поэтому
Т3 = T3, 1 + T3, 2(6)
где
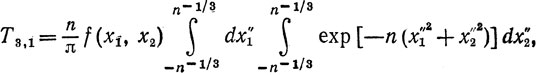
(7)
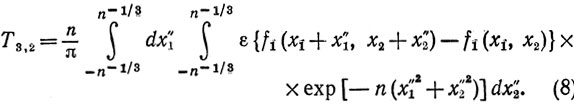
(8)
Для n>max(n0, n1, n2) мы имеем
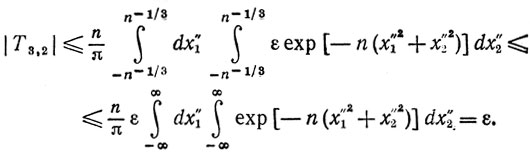
(9)
Двойной интеграл в (7) равен
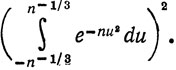
(10)
Но
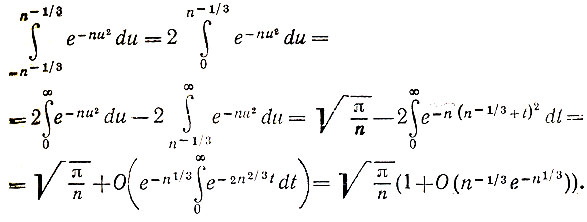
Поэтому легко видеть, что
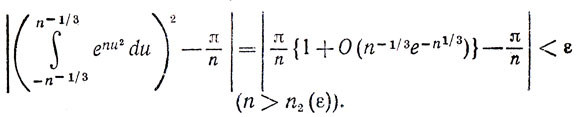
Из (10) и (7) теперь следует, что
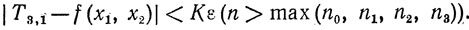
(11)
Из (2)-(11) же следует, что
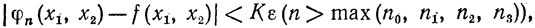
и (1) доказано.
"Цивилизованное" доказательство выглядит так.
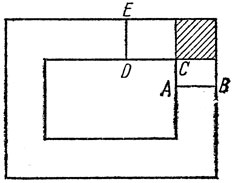
Рис. 7
Распространим определение f(x, y) на больший прямоугольник R+; пусть, например, на АВ (рис. 7) f равно f(A), а в заштрихованном квадрате f = f(С). Новая функция f непрерывна в прямоугольнике R+.
Для (x, y) из R положим
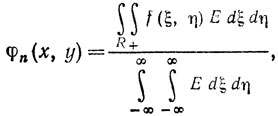
(12)
где E = ехр [-n {(ξ-x)2 + (η-y2)}]. Знаменатель есть постоянная πn-1 (не зависящая от х, y); следовательно, (12) записывается в виде
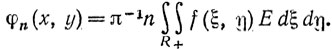
(13)
Вклады в числитель и знаменатель правой части формулы (12), вносимые областями, лежащими вне квадрата S = S(x, y) со стороной n1/3 вокруг точки (х, y), экспоненциально малы. Так как сам знаменатель равен πn-1, то мы имеем (все o равномерны)
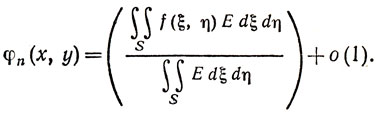
Так как S мало, то f(ξ, η) в последнем числителе равно f(x, y) + o(1); итак, окончательно, φn, определенное в (12), представимо в виде φn(x, y) = f(x, y) + o(1), что и требовалось доказать.
Вторая часть доказательства теоремы Вейерштрасса проводится так. Для подходящего N = N(n) мы при всех (х, y) из R и всех (ξ, η) из R+ имеем
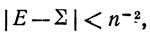
где
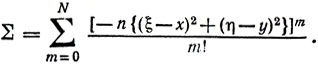
Тогда
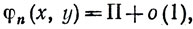
где
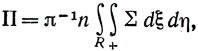
очевидно, является многочленом от х, y.
Старые авторы работали с аппаратом и обозначениями которые мы находим невыносимо неуклюжими. Типичным примером является данное Коши доказательство теоремы что всякое алгебраическое уравнение имеет корень. Современный вариант, который может быть сжат до полстраницы, дан в книге Харди Г. Х. Курс чистой математики.- М.: ИЛ, 1949. Приложение II. Идеи все принадлежат Коши, но ссылка на него должна выглядеть так: Exerclses.- T.4.- P. 65-128-64 страницы (и все существенны, хотя Коши попутно дает много нового). Чтение текста Коши не облегчается тем обстоятельством, что то, что мы бы сейчас обозначили 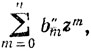 имеет вид
имеет вид
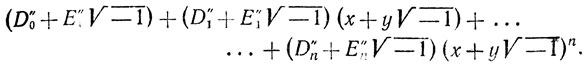
Постскриптум о чертежах. "Картинное" определение на рис. 7, являясь естественным источником идеи, может быть с той же непосредственностью дано словами: "определим f вне R так, чтобы она имела значение, равное ее значению в ближайшей точке R"; словесное определение можно использовать в печатном тексте с целью уменьшить стоимость типографских работ, но в лекционном изложении необходим чертеж. Он служит здесь "текстом для проповеди". Мои ученики упорно не хотят пользоваться чертежами даже в неофициальном порядке, когда это для них не связано ни с какими затратами. Эта практика распространяется; недавно я обнаружил, что она существует уже более 30 лет, а также открыл ее причину. Было принято делать серьезное предупреждение*, что чертежи не должны использоваться в строгих рассуждениях; этот блеф никогда не подвергался проверке, и его жертвы по вине перестраховщиков остались напуганными навсегда. Конечно, некоторые чертежи не могут служить основанием для строгих рассуждений, но я бы сказал, что большинство чертежей может (и я использую такие чертежи, когда только возможно). Использование графика для определения неприятной функции (например, ведущей себя по-разному на разных отрезках) является, очевидно, законным; недавно мне пришлось прокладывать себе дорогу через определение, вполне сравнимое с данным выше "плохим" определением, тогда как график рассказал бы всю историю в несколько секунд. Этот способ использования чертежей не отличается по существу от таких принятых условностей, как "юго-западный угол" Но более того, рассуждения, основанные на графиках, хотя и не столь признаны, также могут быть вполне законными. Возьмем теорему*: из f(x) = o(1) при x→∞ и f" = O(1) следует, что f' = o(1). Если f' ≠ o(1), график y = f'(х) будет иметь для произвольно больших х "пики" (над или под y = 0), содержащие треугольники типа PQR (рис. 8), в которых высота Р не мала, наклоны сторон PQ и PR не велики и, следовательно, площадь PQR не мала. Тогда f(Q) - f(R) не мало, а это противоречит тому, что f = o(1). Это рассуждение строго (и достойно печатного текста) в том смысле, что при переводе его в символы мы не встретим ни одного шага, который не был бы однозначно определен и тривиален. Я сам всегда думаю так, когда материал это позволяет.
* (Чтобы отучить от "школьной математикам.)
** (Увы, не Дж. И. Литлвуда, хотя я ее переоткрыл, и это было важным моментом в моей карьере. Я упоминаю о ней потому, что я получил ее, используя графическое рассуждение.)
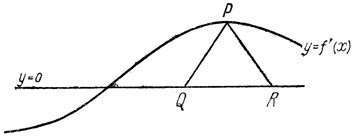
Рис. 8
Одним из лучших графических рассуждений является доказательство одномерной теоремы о неподвижной точке: Пусть функция f(x) непрерывна и возрастает для 0≤х≤1, причем 0≤f(x)≤1, и пусть f2(x) = f {f(x)}, fn(x) = f {fn-1(x)}. Тогда при итерациях f либо каждая точка является неподвижной, либо стремится к неподвижной точке.
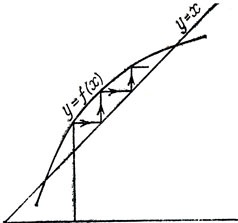
Рис. 9
Для профессионала все, что нужно для доказательства, имеется на рис. 9.*
(Сообщено д-ром А. Е. Уэстерном.) Начиная с 1914 г. действовал парламентский акт о домовладениях, содержавший следующее определение (мои обозначения в скобках). "Стандартная плата" (R) была определена как плата, взимавшаяся в 1914 году (R0), если эта последняя не была меньше определенной суммы (V); в противном случае стандартная плата должна была совпадать с этой суммой. "Дом подпадает под действие акта, если либо стандартная плата, либо эта сумма меньше 105 фунтов стерлингов". Было много судебных дел, которые разбирались по отдельности в каждом случае. Положение определялось фундаментальной теоремой, неизвестной законодателям.
Теорема. Дом подпадает под действие акта тогда и только тогда, когда V≤105.
Это следует из леммы*:
Лемма, min {max(R0, V), V} = V.
* (min (а, b) - меньшее, max (а, b) - большее из чисел а и b)
12.Опечатки. Недавний номер журнала Observatory содержал следующую очаровательную "типичную заметку":
"Профессор Оффорд и я недавно пропустили забавную опечатку (Annals of Mathematics (2), 49, 923, 1.5). В доказательстве знак плюс превратился в знак умножения. Получившаяся неверная формула послужила основой следующего за ней ошибочного рассуждения. (В свое оправ-[ние заметим, что справедливость окончательного резуль-га была известна.)"
В Mathematical Gazette.- V. 14.- P. 23 помещена заметка У. П. Милна "Noether's Canonical Curves", в которой ссылается на "статью Guyаеlf // Proc. London Math, с, Ser. 2.- V. 21, Part 5". Guyaelf - автор-призрак; указанная статья принадлежит У. П. Милну.
Однажды я предложил Харди найти опечатку на одной странице нашей общей работы. Он не мог ее найти. Ошибка была в его собственном имени: "G. H. Hardy".
В докладной записке, которую я написал (около 1917 года) для Баллистического управления, в конце была фраза "Таким образом, σ следует сделать сколь возможно малым". В печатном тексте записки этой фразы не было. Но П. Дж. Григг сказал: "Что это такое?" Едва заметное пятнышко на пустом месте в конце оказалось миниатюрнейшим σ, которое я когда-либо видел (наборщики, вероятно, разыскал и весь Лондон).
В музыке* проблеск гения может показаться простой опечаткой (быть может, ля-диез в 224 такте первой части сонаты оп. 106 Бетховена?). Может ли это произойти в математике? Я могу предложить гипотетический случай. Было время, когда никто не думал о возможности рассмотрения бесконечных систем интервалов и под "системой интервалов" всегда понимали конечную систему. Вообразим определение "содержания" точечного множества Е как "точной нижней грани суммарной длины системы интервалов, содержащих Е". Допустим, что некий ригорист, придравшись к отсутствию слова "конечной", спросил бы себя "а что, если допустить бесконечные системы"? Он сделал бы первый шаг по пути, неукоснительно ведущему к мере Лебега.
* (Или литературе: "Light falls from the (h)air"?)
13.Фразеология. Недавно была опубликована статья, в начале которой имеется фраза: "Целью настоящей статьи является доказательство [чего-то весьма важного]"*. Только в конце читатель с некоторым трудом уясняет себе, что "цель" эта остается недостигнутой**.
* (Я часто думал о том, каким интересным было бы литературное . соревнование по составлению сочинения, по прочтении которого вначале казалось бы, что автор совершает множество ошибок, связанных с неправильным словоупотреблением, но где в действительности все было бы верно (причем установление этого требовало бы известного труда).)
** (Автор не имел никаких неблаговидных намерений, он просто вкладывал в свои слова не совсем обычный смысл.)
Из одной прекрасной книги по астрономии: "Многие из спиральных галактик, в отличие от эллиптических, показывают яркие линии благодаря, несомненно, присутствию или отсутствию газообразных туманностей".
[Этот богатый комплекс несуразностей заслуживает внимательного анализа. В основном он является незаконной комбинацией корректной фразы: "спирали показывают яркие линии благодаря присутствию..." и некорректной фразы: "эллипсоидальные галактики не показывают ярких линий благодаря отсутствию...".]
Литературный обычай передавать словами числа, меньшие 10, оказывается в математике часто весьма неудобным (хотя здесь можно проводить тонкие различия). В- настоящее время злоупотребление словесной формой, к сожалению, весьма распространено. Недавно я обнаружил (у весьма наивного автора) фразу: "функции, никогда не принимающие значений нуль или единица". Сам я предпочитаю почти всегда применять цифры (и следую этому в настоящей книге).
Лингвист с ужасом узнает, что если множество не замкнуто, то это еще не означает, что оно открыто, или же, что "E плотно в Е" - не то же самое, что "E плотно в себе".
"Где X большое очень мало"*.
* (В одном распространенном учебнике математического анализа есть такая фраза: "Проинтегрируем это выражение по х от х = а до х = х".- Примеч. пер.)
Я хотел было включить несколько эффектных парадоксов, связанных со словом "ничего", но затем решил, что они слишком легковесны.
Устное слово опасно. Одна знаменитая лекция была совершенно непонятна большинству аудитории потому, что "Ханю",- несомненно, важное действующее лицо в драме - не сразу отождествлялось слушателями о hv.
Мне приходилось читать вслух фразу "где Е!- любое штрихованное множество"*.
* (В английском тексте игра слов: "dashed" одновременно означает "снабженное штрихом" и "проклятое".- Примеч. пер.)
14.Шутки и т. п. Все рефлексивные парадоксы являются, конечно, превосходными шутками. Я начну с двух классических парадоксов, хотя они хорошо известны.
(а) (Ришар). Должны сущеетвовать (положительные) целые числа, которые не могут быть заданы фразами, состоящими менее, чем из шестнадцати* слов. Любое множество положительных целых чисел содержит наименьшее число, и поэтому существует число N, "наименьшее целое число, которое не может быть задано фразой, состоящей из менее, чем шестнадцати слов"**. Но эта фраза содержит 15 слов и определяет N.
* (Не "16" в силу вполне достаточных, хотя и весьма тонких причин.)
** (Пример, естественно, пришлось заменить.- Примеч. пер.)
(b). (Вейль). Большинство английских прилагательных не обладает качеством, которое они обозначают; прилагательное "красный" само не красное. Однако некоторые прилагательные обладают тем качеством, которое они обозначают; например, прилагательное "adjectival"*. Назовем прилагательное первого типа гетерологическими, а второго - гомологическими. "Гетерологический" - прилагательное; к какому типу оно принадлежит?
* (Или, скажем, русское прилагательное "выразительный".- Примеч. пер.)
В журнале Spectator был объявлен конкурс на тему: "Что бы Вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?". Первый приз получил ответ:
"Наш второй конкурс Первый приз во втором конкурсе этого года присужден мистеру Артуру Робинсону, остроумный ответ которого без натяжки должен быть признан наилучшим. Его ответ на вопрос: "Что бы Вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?" был озаглавлен "Наш второй кон курс", и состоял в следующем: "Первый приз во втором конкурсе этого года присужден мистеру Артуру Робинсону, остроумный ответ которого без натяжки должен быть признан наилучшим. Его ответ на вопрос: "Что бы Вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?" был озаглавлен "Наш второй конкурс", но из-за лимитирования бумаги мы не можем напечатать его полностью".
Следующая идея возникла слишком поздно (не помню кому она пришла в голову), но должно было случиться вот что. Я написал работу для Comptes Rendus, которую проф. М. Рисс перевел для меня на французский язык. В конце было три подстрочных примечания. Первое (на французском языке) гласило: "Я весьма признателен проф. Риссу за перевод настоящей статьи". Второе гласило: "Я признателен проф. Риссу за перевод предыдущего примечания". Третье гласило: "Я признателен проф. Риссу за перевод предыдущего примечания" и так, казалось бы, нужно продолжать до бесконечности. В действительности я законно ограничился примечанием № 3: сколь плохо я ни знаю французский язык, я в состоянии переписать французскую фразу.
Учитель: "Предположим, что х есть число овец в задаче". Ученик: "Но, господин учитель, предположим, что х не есть число овец". Я спросил проф. Виттгенштейна, не имеет ли эта шутка глубокого философского смысла, и он ответил, что имеет.
(А. С. Безикович.) Репутация математика основывается на числе плохих доказательств, которые он придумал. (Работы первооткрывателей неуклюжи.)
"Я хотел бы сказать, насколько я обязан мистеру Смиту в связи с этой работой". Так скажите!
Эквивалентность и тождественность. Сколько математиков применяет символ О(1), не отдавая себе отчета в том, что с ним связана одна подразумеваемая условность? Верно, что sin х = О(1)) но нельзя сказать, что o(1) = sin x.
Начиная с 1910 г. время от времени ставится вопрос об исключении задач по оптике и астрономии из экзаменационных билетов. Было обнаружено, что в течение ряда лет ни один из студентов, занявших первые места, не пытался решать задачи по этим предметам. Этому утверждению можно придать эквивалентную форму: никто из студентов, решавших эти задачи, не смог занять первого места.
"Мы все знаем, что люди иногда делают лучшие вещи, чем все, что они делали раньше, но г-н N сделал лучшую вещь, чем все, что он может сделать". [Фактическая цитата, причем специалисты соглашаются с ней по всем пунктам.]
Один слишком старательный аспирант спросил, необходимо ли прочитать всю литературу прежде, чем начать писать работу. "Ничто не является необходимым или достаточным". Вторая часть (содержащая горькую истину: глубокий эрудит может быть лишен творческого начала) возникает просто по инерции в связи с чисто словесной ассоциацией.
"Не делай недовольной мины при звуках сонаты какого-нибудь великого князя: ты никогда не знаешь, кто в действительности написал ее" (Гайдн). (По поводу одной отвергнутой докторской диссертации.)
Один слишком навязчивый аспирант довел своего руководителя до того, что тот сказал ему: "Идите и разработайте построение правильного многоугольника с 65 537* сторонами". Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением (которое хранится в архивах в Геттингене).
* (65 537 = 216 + 1.)
Лет 25 назад я слышал не столь печальную историю, за истинность которой, впрочем, ручаться не могу. В ней рассказывалось о том, что первое применение кристалла как дифракционной решетки явилось результатом принятой всерьез шутки. (Помню, как я по поводу утверждения, что нельзя переносить наивные предрассудки обыденной жизни, например, в астрофизику, говорил себе следующее: "будь готов рассматривать Солнце как твердое тело или внутренность Земли как идеальный газ". В те времена звезды рассматривались в лучшем случае как газы, весьма далекие от идеальных.)
Эразм Дарвин считал, что время от времени следует производить самые дикие эксперименты. Из них почти никогда ничего не выходит, но если они удаются, то результат бывает потрясающим.
Дарвин играл на трубе перед своими тюльпанами. Результат этого эксперимента оказался отрицательным.
"X нашел, что в этих условиях возникают гравитационные волны; однако есть предположение, что в работе содержится ошибка".
Ясно, что всякая ошибка порождает гравитационные волны.
Ландау* заготовлял печатные формуляры для рассылки авторам доказательств последней теоремы Ферма: "На стр. ..., строке ... имеется ошибка". (Находить ошибку поручалось доценту.)
* (Речь идет об известном немецком математике Эдмунде Ландау.- Примеч. пер.)
Один педантичный профессор имел обыкновение говорить: "...полином четвертой степени
ах4 + bx3 + сx2 + dx + e,
где е не обязано быть основанием натуральных логарифмов" (но может им быть).
О книгах Жордана говорили, что если ему нужно было ввести четыре аналогичные или родственные величины (такие, как, например, а, b, с, d), то они у него получали обозначения a, MS, ε2, Π"1, 2.
Классификация углов из книги по альпинизму (около 1900 г.):
- перпендикулярно - 60°,
- Мой дорогой сэр, абсолютно перпендикулярно - 65°,
- нависающе - 70°.
Я прочел в гранках книги Харди о Раманужане: "кто-то сказал, что каждое положительное целое число было одним из его личных друзей". Моей реакцией на это место было: "Интересно, кто это сказал; я бы хотел, чтобы это был я". В верстке я уже прочитал (так, как это теперь напечатано) "Литлвуд сказал...".
(Произошло следующее: Харди выслушал мое замечание молча, с непроницаемым лицом, так что я решил, что он пропустил его мимо ушей. Впоследствии я упрекнул Харди в том, что он вообще имеет привычку часто не реагировать на замечания, на что он ответил: "Что же остается делать? Неужели каждый раз говорить: вот это здорово!" Ответ: "Да".)
Закончу одной моей шуткой, которую я всегда с удовольствием вспоминаю. Веблен как-то читал 3 лекции по геометрии путей; в конце одной из них уравнения путей чудесным образом приняли форму
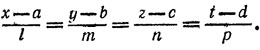
Он закончил сообщением о том, что будет следовать дальше, и сказал: "Я буду действовать как сам Иоанн Креститель". Смысла этих слов (ответственности за который я никоим образом не несу) я уже не помню" но я воспользовался посланной небом возможностью сказать: "Поскольку наши пути прямые".
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'