Из экзаменационных билетов по математике

7. Всегда приятно наблюдать, как другие совершают глупости, которые когда-то делал сам. Следующий вопрос был включен в один из билетов в 1924 г.

(а)^* Эллипсоид, окруженный идеальной однородной жидкостью, начинает двигаться в произвольном направлении со скоростью V. Показать, что если внешняя граница жидкости - неподвижный софокусный эллипсоид, то количество движения, приобретаемое жидкостью, равно - MV, где М - масса жидкости, вытесненной эллипсоидом.

^* (Пусть любитель смело читает дальше.)

Позже этот результат был распространен на другие пары поверхностей, в частности на две соосные поверхности вращения.

Каковы бы ни были две поверхности, о которых идет речь в задаче, мы всегда можем представить себе внутреннюю заполненной той же жидкостью; тогда центр масс будет неподвижен.

Опубликованные сборники экзаменационных вопросов содержат (и не случайно) не те вопросы, которые были фактически заданы, а те, которые должны были бы быть заданы; редкий год обходится без Поправок. Однажды один из вопросов был так безнадежно неверен, что мы заменили его безобидным пустяком.

В прошлом в экзаменационных билетах по второй части экзамена были задачи "со звездочками" (современный стиль), указывавшими на их легкость и на то, что очки, полученные за их решение, не засчитываются при распределении первых мест. Был случай, когда одна задача со звездочкой была предложена, отвергнута, вновь предложена и вновь отвергнута как слишком трудная для включения ее даже без звездочки. В конце концов она вошла в билеты по третьей, наиболее трудной, части экзамена.

Однажды, присутствуя на письменных экзаменах, я заметил, что розданные таблицы логарифмов не содержат значений е и lg e = 0,4343, тогда как в билете требовалось доказать, что нечто имеет численное значение 4,343 (в действительности речь шла о значении 10 lg e). Должен ли был I я сообщить недостающую информацию, учитывая, что такое сообщение было в данном случае явно наводящим? После некоторого колебания я все же сделал соответствующее объявление, но по недосмотру совершил несправедливость, забыв передать его в другой зал, где писали работу студентки.

8. Я унаследовал старые "Экзаменационные книги" Роуза Болла, относящиеся к началу 80-х годов прошлого столетия. Кое-что в них может представить интерес. В январе на 4 курсах проводился экзамен, состоявший из 18 трехчасовых работ. В один из этих годов максимальное возможное число очков составляло 33541; первое место было получено за 16368 очков, второе - за 13188, последнее призовое место - за 3123 очка. Последний в списке (за номером девяносто с чем-то) получил 247 очков. Первый вопрос был оценен в 21 очко, во второй работе (по решению задач) был вопрос в 500 (>2*247) очков.

Будучи упорным противником старой экзаменационной системы, я был несколько раздосадован, когда обнаружил, что в ней есть много разумного. Для меня было неожиданностью, что студент, занимавшийся только "зубрежкой" (в почти современном объеме), не мог подняться выше 23-го места, хотя экзаменаторы 80-х гг, и поддавались иногда соблазну ставить вопросы, требовавшие лишь непосредственного приложения книжных знаний. Две работы по решению задач, за выполнение которых можно было получить большое число очков, были для такого студента очень серьезным препятствием; если ему удавалось получить по ним, скажем, четверть того числа очков, которое присуждалось за их лучшее решение, то он уже продвигался примерно до 20-го места. (Около 1905 г. соответствующие цифры были такими: 14-е призовое место из 26 за чисто книжные знания, причем в случае получения 7 % очков за работы по решению задач студент продвигался до 11-го места, опережая при этом мистера Д. М. Кейнса^*.)

^* (Известный английский буржуазный экономист.- Примеч. пер.)

9. Рассматривая задачи, в особенности повышенной трудности, с точки зрения требуемой для их решения виртуозности (в поисках задач с каким-либо подвохом), я опять-таки был разочарован тем, что их оказалось немного. Однако две задачи остались в моей памяти.

(b) Сфера, вращающаяся с трением на верхней образующей горизонтального цилиндра, находится в равновесии; легким толчком ее выводят из состояния равновесия; доказать, что точка касания сферы и цилиндра начнет описывать на цилиндре винтовую линию.

*Развивая эту идею, в следующем году (утренний экзамен 18 января 1881 г.) экзаменатор предложил доказать следующее утверждение (привожу его в моей формулировке):

(с) Если распределение масс в сфере, вращающейся на образующей горизонтального цилиндра, обладает центральной симметрией, т. е. плотность зависит только от расстояния до центра, то траекторией точки касания цилиндра и выведенной из равновесия сферы является винтовая линия на цилиндре до самой точки отрыва. [200 очков; вторая часть вопроса, требовавшая некоторых дальнейших уточнений, была оценена дополнительно в 105 очков.]*

Относительно задачи (и) возникает вопрос, нельзя ли ее так же "убить", как задачу (а). Выйдя на прогулку вскоре после ознакомления с задачами (и) и (с), я присел отдохнуть на бревно. В результате некоторого процесса ассоциации в моей голове возникла задача (b) и блеснула следующая мысль. Утверждение "точка касания начнет описывать винтовую линию" означает, что кривизна и кручение стационарны в наивысшей точке Р; продолжим траекторию назад; так как она симметрична относительно точки Р, то кривизна и кручение должны быть стационарны в точке Р. Теперь я спрашиваю: является ли это доказательством или, быть может, основой возможного доказательства, сколько очков я получил бы за него, и как скоро вы дадите ответ на эти вопросы?

*10. Перейдем к (с). Я не считаю, что эта задача^* содержит подвох: ее решение требует лишь применения общих теорем относительно движущейся системы координат, причем одно любопытное совпадение приводит к тому, что окончательное уравнение решается; все это легко усмотреть, если ответ дан. Этот чрезвычайно изящный результат, по-видимому, недостаточно широко известен.

^* (В оригинальной формулировке закон распределения масс был задан, причем требовалось вычислить момент инерции и некоторые другие детали.)

Возьмем движущуюся систему координат с началом в центре сферы с осью Оy по нормали в точке касания и осью Оz параллельно образующей цилиндра. Пусть ось Оy образует с вертикалью угол θ. Исключая силы реакции в точке касания (см. Lamb. Higher Mechanics, с. 165-166), мы получим

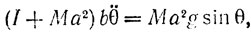
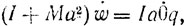
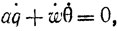
или, полагая а = 1,

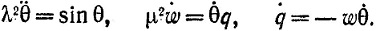
Второе и третье уравнения дают

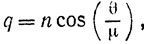
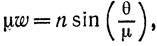
где 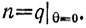Ели μ = 2, то комбинация этих результатов с первым уравнением приводит к 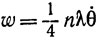и, следовательно, к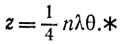

Предположим, что сфера начинает катиться внутри вертикального цилиндра (сила тяжести учитывается, но диссипативные силы отсутствуют); что произойдет? Единственной разумной догадкой является спиральный спуск возрастающей крутизны; в действительности же сфера будет двигаться вверх и вниз между двумя фиксированными горизонтальными плоскостями. Игрокам в гольф не так уж не везет, как они думают.

Около 1911 г. экзаменатор A предложил вопрос: Е и W - партнеры в бридже; допустим, что Е не имеет на руках туза, но получил информацию, что у W есть туз; какова тогда вероятность р того, что у W по крайней мере 2 туза? Коллега В, проверяя ответ А, получил другое значение вероятности. Выяснилось, что В вычислил вероятность q того, что W имеет по крайней мере два туза в предположении, что у W туз пик. Вероятности р и q различны, и q>p.

Предполагая все время, что у Я на руках нет ни одного туза, заметим, что 1-q есть вероятность того, что W имеет одного только туза пик, деленная на вероятность того, что W имеет по крайней мере туза пик: в то же время 1-р есть вероятность того, что W имеет только одного туза, деленная на вероятность того, что W имеет по крайней мере одного туза. Второй числитель в 4 раза больше первого. Следовательно,

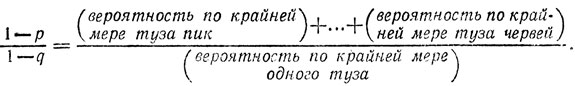
Так как события, фигурирующие в числителе, не исключают друг друга, то это отношение больше 1.

Кажущаяся очевидность ошибочного заключения "p=q" возникает из рассуждения: "W имеет туза; мы можем предположить, что это туз пик". Но этого "это" не существует; если № имеет более одного туза, то тот, кто дает информацию игроку Е, должен выбирать одного из тузов, чтобы его можно было принять за "это". Ситуация становится яснее, когда играющему сдают 2 карты из колоды, состоящей из 3 карт: туза пик, туза червей и двойки бубен. Здесь мы уже во всяком случае знаем, что один туз должен быть на руках, и вероятность двух тузов равна ¹/₃. Если же мы знаем, что на руках есть туз пик, то вероятность двух тузов равна ¹/₂.