Математика с минимумом "сырого материала"

1. Какие вопросы настоящей математики могут попасть в такой раздел? Условием sine qua non несомненно является то, что результат должен быть понятен любителю. Мы не должны настаивать на том, чтобы и доказательство было доступно (см., например, п. (15), (16), (19)), хотя чаще всего и это имеет место. Я начинаю с бесспорных случаев; дальше выбор становится уже более трудным, и последние примеры включены потому, что по разным причинам они мне нравятся. Некоторые вопросы, необходимые для полноты картины, только "упоминаются" или же рассмотрение их откладывается.

(1) "Общеизвестное" евклидово доказательство бесконечности множества простых чисел может, конечно, претендовать на первое место (см., например, Hardy Q. Н. A mathematician's apology, с. 32-34 или с. 22 ниже).

В этом пункте могли бы найти себе место и "известные" вещи из § 3, но для того, чтобы сделать их понятными для любителя, потребовалось бы прервать изложение.

Первое место я все же отвожу хорошо известной задаче-шутке, покорившей Европу много лет назад и опубликованной в той или иной форме во многих книгах. Я обращаюсь к ее первоначальной формулировке, согласно которой внезапная мысль, возникающая у А, порождается эмоциональным стимулом.

(2) Три дамы А, В и С сидят в купе железнодорожного вагона с испачканными лицами и все три смеются. Внезапно А соображает: почему В не понимает, что С смеется над ней?- О боже! Они смеются надо мной. (Формально: если я, А, не выгляжу смешной, то В должна рассуждать так: если я, В, не выгляжу смешной, то С не над чем смеяться. Так как В так не рассуждает, то, следовательно, я, А, выгляжу смешной.)

Это - настоящее математическое рассуждение, и, уж несомненно, с минимумом материала. Но, более того,- что, насколько мне известно, не попало ни в какие книги,- в принципе возможно обобщение на случай n дам с испачканными лицами и смеющихся.

По индукции: в (n+1)-ситуации А рассуждает: если я не выгляжу смешной, то В, С, ... образуют n-ситуацию и В должна была бы перестать Смеяться, но этого, однако, не происходит.

Сравните с правилом поджаривания трех кусков хлеба на сковородке, вмещающей только 2 куска: A₁, B₁; затем В₂, С₁; затем С₂, A₂. Это не дотягивает до математики.

(3) Следующий пример, вероятно, не выдерживает строгой критики, но при доброжелательном отношении занимателен.

Имеется неограниченное количество карт, на противоположных сторонах которых написаны числа 1 и 2, 2 и 5, 3 и 4 и т. д. Берут произвольную карту и держат между двумя игроками А и В так, что каждый из них видит только одну сторону карты. Каждый игрок имеет право спасовать (т. е. отказаться от игры). Если же оба игрока соглашаются играть, то выигрывает тот из них, который видит большее число. В этой игре каждый рад один из игроков должен пасовать: если А видит 1, то на обратной стороне стоит 2, и он должен пасовать; если он видит 2, то на обратной стороне 1 или 3; если там 1, то В должен пасовать; если же он этого не делает, то пасовать должен А. И так далее по индукции.

(4) Аналогичным примером является следующий (Шрёдингер). Имеется бесконечное количество таких же карт, как в (3), но на этот раз для каждого n карт типа (n, n+1) имеется 10й, и выигрывает тот из игроков, который видит меньшее число. Предположим, что А и В делают одинаковые денежные ставки. В этой ситуации А "должен" играть, что бы он ни видел на обращенной к нему стороне карты; то же самое, разумеется, справедливо относительно В, причем шанс каждого из них на выигрыш составляет 9 к 1. Это в высшей степени странное заключение вытекает из того, что, какое бы число n ни видел A, в 10 раз вероятнее, что на другой стороне стоит n+1, чем то, что там стоит n-1. (Кстати, какое бы число N ни было задано до того, как карта вынута, бесконечно вероятнее, что на ней будут числа, большие N.)

(5) Парадокс бесконечности. Шары, занумерованные числами 1, 2, ... (для математика - сами эти числа), кладутся в ящик следующим образом. За одну минуту до полудня кладутся числа от 1 до 10, и число 1 вынимается обратно. За ¹/₂ минуты до полудня кладутся числа от 11 до 20, и число 2 вынимается обратно. За ¹/₃ минуты до полудня кладутся числа от 21 до 30, и число 3 вынимается обратно, и т. д. Сколько чисел останется в ящике в полдень? Ответ: ни одного. Какое бы число мы ни назвали, например 106, оно отсутствует в ящике, так как оно вынимается при 106-й операции.

* Аналитик постоянно встречается с таким положением вещей; посмотрев на множество точек

он сразу скажет, что оно "пустое", не видя в этом ничего парадоксального.*

В связи с парадоксами я хотел бы сделать экскурс в небесную механику. Предположим, что n тел, рассматриваемых как точки, движутся по законам ньютоновского тяготения. Системы, в которых рано или поздно произойдет простое столкновение (столкновение только двух точек^тел), бесконечно редки^*. Ни в чем нельзя быть более уверенным, чем в том, что то же имеет место для кратных столкновений (т. е. столкновений трех или более точек-тел). (В самом деле, в то время как простые столкновения являются нормальным явлением для закона обратных кубов, кратные столкновения, несомненно, бесконечно редки при любом законе.) Тем не менее доказательства нет.

^* (На математическом языке: множество "точек-представителей" (в пространстве начальных условий) систем, в которых возможны простые столкновения, имеет меру 0.)

Это, конечно, парадокс относительно доказательств, а не относительно фактов. Можно также его объяснить. При простых столкновениях аналитический характер поведения обобщенных соответствующим образом систем сохраняется, а отсюда можно усмотреть, что простое столкновение (как бы поздно оно ни произошло) влечет за собой два аналитических соотношения между начальными условиями, что и делает эти условия бесконечно редкими.

2. (6) 4 корабля А, В, C и D плывут в тумане с постоянными и различными скоростями на прямолинейных и различных курсах. Пять пар А и В, В и С, С и A, В и D, С и D чуть не столкнулись; назовем это "столкновениями". Большинство людей находят неожиданным математическое следствие, что при этих условиях А и D также должны обязательно "столкнуться". Рассмотрим трехмерные графики положений в системе координат плоскость движения - время (так называемые "мировые линии"), причем ось времени будем представлять себе вертикальной. Мировые линии a, b, c с попарно пересекаются, следовательно, они лежат в одной плоскости, скажем, плоскости р; d пересекается с b и с е, так что она тоже лежит в плоскости р, и поэтому должна пересечь а. (Кратные столкновения по условию исключаются. Параллельность двух мировых линий не может иметь места вследствие различия скоростей.)

(7) Эксперимент, доказывающий вращение Земли. Стеклянная трубка, имеющая форму кольца, наполнена водой и расположена горизонтально, для простоты, на северном полюсе. Трубка внезапно поворачивается на 180° вокруг горизонтальной оси. Вода теперь течет по трубке (со скоростью один оборот в 12 часов) и ее движение может быть обнаружено. Это могло бы быть изобретено Архимедом, но должно было ждать своего открытия до 1930 г. (А. Н. Compton). Интересно отметить, что многие экспонаты из моей коллекции возникли сравнительно недавно, Для разнообразия: дата открытия следующего факта - 1605 г.

(8) Стевин и сила тяжести на наклонной плоскости. Цепь ABCD, висящая, как показано на рис. 1, должна находиться в равновесии (иначе мы имели бы вечное движение). Симметричная нижняя часть ADC может быть отброшена, так как она оказывает одинаковое воздействие на АВ и ВС. ABC остается в равновесии. Этот факт равносилен закону синуса. (Интересное обсуждение этого вопроса имеется в книге: Масh E. Science of Mechanics, с. 24-31.)

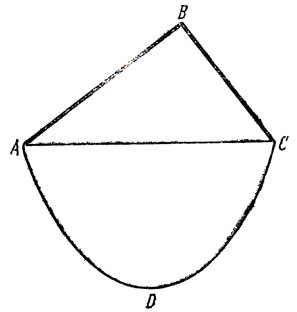
Рис. 1

(9) Чтобы определить орбиту планеты или кометы, достаточно трех наблюдений, каждое из которых дает две (угловые) координаты и время t. Фактически любой системе наблюдений (направьте как угодно телескоп в любые 3 момента времени) соответствует орбита^*. Представим себе пятнышко на объективе телескопа; оно дает такие же результаты наблюдений и также описывает орбиту (Земли). Но уравнения для элементов орбиты сводятся (если ^опустить некоторые технические детали) к уравнению 8-й степени. Это уравнение должно иметь вещественный корень. Но так как его степень четная, то оно должно иметь и второй вещественный корень.

^* (Коническое сечение с Солнцем в фокусе)

Это, по всей видимости, строгое рассуждение является пробой математического вкуса. Между прочим, шутка здесь не только по поводу математики, ее соль - в самой математике.

(10) Разбиение квадратов и кубов на конечное число квадратов и кубов, среди которых нет равных. Разбиение квадрата возможно бесконечным множеством различных способов (простейший из них очень сложен); разбиение куба невозможно. (Поэтому вопросу см. Brooks R. L., Smith С. А. В., Stone А. Н., Тutte W. Т. The Dissection of Rectangles into Squares // Duke Hath. J.- 1940.- V. 7.- P. 312.) Поразительное доказательство первого результата очень сложно. Авторы дают следующее элегантное доказательство второго утверждения. В разбиении квадрата наименьший квадрат не может быть у стороны разбиваемого квадрата (очевидно). Предположим теперь, что разбиение куба существует. Кубы, стоящие на нижней грани, производят разбиение этой грани и наименьший из этих кубов стоит на квадрате, лежащем целиком внутри грани. Верхняя грань этого куба окружена стенами, на ней должны стоять кубы, возьмем из них наименьший и т. д.- процесс продолжается без конца. (Если, однако, мы спросим, может ли куб быть полностью окружен большими неравными кубами, то ответ будет положительным.)

(11) Парадокс с голосованием!^*. Если человек не принимает участия в голосовании на том основании, что его шансы повлиять на результат пренебрежимо малы, то обычно его упрекают, говоря "а допустим, что все поступят так". То, что этот упрек принципиально ошибочен, является неприятной истиной, к счастью, скрытой от большинства человечества. Рассмотрим соответствующие величины в случае, когда результат голосования относительно проблематичен. Шанс, что голос данного избирателя приведет к избранию его кандидата, равен примерно 1 к 5000; есть также дальнейший шанс порядка 1 к 50, что этот результат приведет к смене правительства. Полный шанс последнего события не меньше, чем 1 к 250 000. Так как мы имеем 30 000 000 голосующих с одинаковыми возможностями, то может показаться, что здесь что-то не так; объяснение заключается в том, что когда это событие вызвано голосованием данного избирателя, то приблизительно 20 000^** других избирателей этого округа находятся в таком же положении.

^* (Здесь речь идет о выборах членов палаты общин английского парламента.- Примеч. пер.)

^** (Половина 70% от 60 000. Расчет ведется на среднее число лиц, имеющих право голоса в одном округе, избирающем члена палаты общин, и на средний процент участия в выборах.- Примеч. пер.))

В 1909 г. было внесено предложение, чтобы две партии, поделившие голоса в отношении р к q, были представлены в отношении p³ к q³; это предложение было возобновлено журналом Economist в январе 1950 года, так как ряд предшествовавших выборов хорошо подтверждал это правило. То, что отношение представительства будет, скорее всего, больше отношения голосов, ясно потому, что меньшинство в 49 к 51, разбросанное по округам, не получает ни одного места в парламенте. Таким образом, представительство в парламенте - это вопрос местного распределения сил, а не результат действия какой-либо загадочной причины.

Я готов оспаривать предлагаемое правило. Прежде всего, оно может быть заменено более простым правилом: процент поданных голосов 50±х должен давать процент представительства 50±cx, где в - константа. При с = 3 оба правила практически совпадают до x = 6, а затем начинают расходиться. (При 600 местах большинство в 56:44 дает по правилу кубов 404 места, а по "3-правилу" - 408; при 57:43 получается соответственно 420 и 426.) Этого, вероятно, достаточно для всех практически встречающихся случаев. (Для больших различий в числе голосов следует ожидать в каком-то месте полного исчезновения меньшинства; "3-правило" предсказывает это при отношении 67:33.) Далее, разумно предположить, что при данном распределении сторонников партий в округах увеличение процента с 50±х для голосов до 50±сх для представительства имеет место в пределе при х → 0, и это предельное соотношение может быть распространено на значения x от 0 до 6, причем с надо, очевидно, подобрать так, чтобы получить соответствие с действительностью на дальнем конце интервала. Изменение в распределении сил партий может изменить в (это было написано до выборов в феврале 1950 г., которые показали новое соотношение сил и новое с). Число 3 привлекательно своей простотой, но оно не обязательно. Легко может оказаться, например, что c = 2,9; но все же скорость света и постоянная всемирного тяготения начинаются с цифр 300 и 666.

(12) Задача о взвешивании монет. Эта привлекательная и "по-настоящему математическая" задача была исчерпывающим образом рассмотрена несколько лет назад, и я ограничусь только ее упоминанием (см., в частности, блестящий анализ Смита: Smith G. А. В. // Math. Gaz.- 1947.-V. 31.-P. 31-39.)

3. Как я уже объяснял в п. 1, существуют вещи более "математические" и с более высокими заявками, чем большинство предшествующих, но мы их пропускаем ввиду их "известности". Из топологии назовем (13) лист Мёбиуса, (14) бутылку Клейна, (15) задачу о четырех красках и (16) теорему о жордановой кривой (последние два примера являются весьма крайними случаями, в которых результат почти очевиден, тогда как доказательство очень трудно). Теоремы, доказываемые при помощи "принципа неподвижной точки", также заслуживают упоминания здесь (они рассмотрены в § 5). В книге Что такое математика Куранта и Роббинса^* (KP в последующих ссылках) есть очень интересная глава о топологии, к которой можно отослать заинтересованного читателя.

^* (Русский перевод: Курант Р., Роббинс Р. Что такое математика.- М.: Гостехиздат, 1947. Страницы далее указаны по этому изданию.- Примеч. пер.)

Упомяну также, опять-таки без обсуждения, два открытия Кантора: (17) несчетность континуума и (18) тот факт, что точки линии и точки квадрата образуют "эквивалентные множества", т. е. что они могут быть соединены в пары, иначе говоря, что между этими множествами можно установить взаимно однозначное соответствие (КР, с. 134).

(19) Теорема (Шредера - Бернштейна): если множество А эквивалентно своему подмножеству А₁, то оно эквивалентно и любому "промежуточному" подмножеству, содержащему A₁. В этом случае не только формулировка результата не использует никакого сырого материала, кроме понятия множества, но существует и доказательство* которое не вводит никаких новых понятий (кроме понятий типа "все", опирающихся только на здравый смысл); в нем не упоминаются ни числа, ни последовательности, оно не апеллирует даже к понятию "конечный" (или его отрицанию - "бесконечный"). Тем не менее, доказательство оперирует с этим простейшим сырым материалом с виртуозностью, недоступной для любителя.

Сюда же относятся "рефлексивные парадоксы". Относительно первого парадокса Рассела см. КР, с. 137-138, два других приведены далее на с. 43 (где они фигурируют под рубрикой "шуток"!).

Теперь мы будем все чаще терять компанию любителя, и я прекращаю нумерацию.

*4.Изопериметрическая задача: площадь фигуры, (наибольший) диаметр которой не превосходит 1, не может превышать ^π/₄.

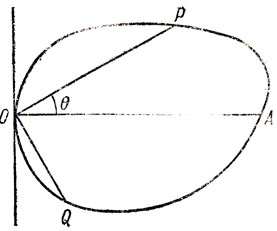
Рис. 2

Существуют различные доказательства. Нетрудно видеть, что мы можем предположить фигуру выпуклой и лежащей по одну сторону от какой-либо ее "касательной". Вводя полярные координаты, как показано на рис. 2, найдем, что

площадь =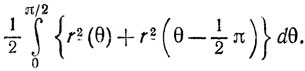

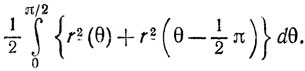
Подынтегральная функция есть OP² + OQ² = PQ² ≤1.

Предположим, что а_n>0 для всех n. Тогда

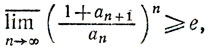
и результат является наилучшим.*

Стержень шарнирно прикреплен к полу железнодорожного вагона и предоставлен самому себе; тогда существует малая, но отличная от нуля вероятность того, что он не упадет в течение двух недель: вероятность равна примерно 1:10¹⁰⁵. (Поезд не предполагается "идеальным": например, он отправляется со станции Кинге Кросс в 3.15, проходит

через туннель, где он 5 минут стоит, а затем, после ряда дальнейших остановок, прибывает в Кембридж в 5.35. Я припоминаю, что мне сообщили, что гений, впервые задавший этот вопрос, не был в состоянии ответить на него.) Доказательство имеется в КР, с 421-423. *Иной способ доказательства (с разумной свободой интерпретации) состоит в следующем. Рассмотрим начальное положение стержня в относительном покое, составляющее угол θ с левым горизонтальным положением. Пусть S будет множеством начальных 6, при которых стержень рано или поздно упадет налево. Основной факт при очень слабых предположениях относительно обстоятельств путешествия и взаимосвязи поезда и стержня (нам нет необходимости детально устанавливать эти предположения) состоит в том, что множество S открыто. Пусть θ₀ - точная верхняя грань углов θ из S. Тогда θ₀ не входит в S, и из начального положения θ₀ стержень никогда не упадет налево. Если же он упадет направо, то он сделает это и для всех θ, несколько меньших θ₀; однако это неверно, так как некоторые (в действительности все) из этих θ принадлежат S. Таким образом, из положения 0О стержень никогда не упадет. А для некоторого, достаточно малого угла вокруг θ₀ он не упадет в течение двух недель.

Поучительно рассмотреть, почему из этого рассуждения не вытекает, что стержень, соответствующим образом установленный в начальный момент, не будет отклоняться, скажем, более чем на 0,5° от исходного положения.*

Это рассуждение моментально убеждает математика. Из всех возможных вариантов избранный мною представляется наиболее подходящим для объяснения любителю.

Допустим, что мы имеем некий набор S (вообще говоря, бесконечный) чисел, или точек прямой, "ограниченный справа"; это значит, что существуют точки Р (расположенные достаточно далеко справа) такие, что ни одна из точек S не лежит справа от Р (в этой формулировке намеренно учтена возможность совпадения точки из S с Р). Любое такое Р называется верхней гранью (короче, в. г.) множества S. Если это имеет место для Р, то это (тем более) имеет место и при сдвиге Р вправо. Если это имеет место для Р₀, но уже не имеет места ни при каком сдвиге Р₀ влево, как бы мал он ни был, то Р₀ называется точной верхней гранью (т. в. г.) S. (Например, 1 является т. в. г. множества чисел, лежащих между 0 и 1, причем безразлично, включается 1 в это множество или нет, а также т. в. г. множества рациональных чисел, лежащих между 0 и 1, с включением числа 1 или без него. Если 1 не включается в эти множества, то т. в. г. не входит в S, если же 1 включается в них, то т. в. г. является элементом множества S.) После небольшого мысленного эксперимента должно стать интуитивно ясным, что каждое множество S, ограниченное справа, имеет т. в. г. Отметим, что имеются два определяющих свойства т. в. г.: (1) она является в. г., (2) ни одна из точек, лежащих слева от нее, не является в. г.

До сих пор задача о стержне не входила в наши рассмотрения (читатель, дочитавший до этого места, познакомился с важным математическим понятием и важной теоремой). Каждый шаг последующего рассуждения может с успехом проверяться на частном случае стоящего поезда: здесь мы знаем ответ - стержень, в начальный момент расположенный вертикально, остается в покое.

Предположим, что в начальный момент стержень находится в состоянии относительного покоя и образует угол θ с левой горизонталью; назовем это "начальным положением θ". Рассмотрим множество S начальных положений 9, из которых стержень рано или поздно упадет налево. Если это происходит с ним при каком-нибудь θ, то то же самое будет иметь место также для всех достаточно близких по обе стороны начальных положений; любое положение θ, принадлежащее к S, находится, следовательно, внутри целого сектора значений 9, принадлежащих к S (на математическом языке: "5 открыто"). Этот интуитивный факт, на котором все основано, имеет место при весьма общих условиях, уточнять которые нет необходимости.

Пусть θ₀ будет т. в. г. множества S. Тогда θ₀ не будет элементом S, так как в противном случае значения θ, находящиеся справа от θ₀ и достаточно близкие к нему, также принадлежали бы к S, и θ₀ не могло бы быть в. г. множества S. Итак, стержень при начальном положении 90 не упадет налево. Но, с другой стороны, если он упадет направо, то он будет падать направо и при всех достаточно близких начальных положениях θ слева от θ₀ (принцип "открытости"), так что никакое из этих начальных положений не может быть элементом S; но это означает, что θ₀ может быть вдвинуто влево, оставаясь при этом в. г. S, что противоречит свойству (2) т. в. г. Следовательно, из исходного положения θ₀ стержень никогда не упадет. А из достаточно малого сектора вокруг θ₀ он не упадет в течение двух недель.

Аналогичный результат верен и при замене обычного шарнира сферическим (позволяющим стержню наклоняться во все стороны). Но в этом случае нам пришлось бы ссылаться уже на значительно более сложную "теорему о неподвижной точке" (КР, с. 335).

Типичной теоремой о неподвижной точке является следующая. Тонкая резиновая оболочка, обтягивающая сферическую поверхность, подвергается деформации без разрывов и складок. Допустим, далее, что никакая точка Р при этом не перемещается в положение Р', диаметрально противоположное исходному. Теорема тогда утверждает, что должна существовать по крайней мере одна "неподвижная точка" (т. е. такое Р} для которого Р' - "образ" Р - совпадает с Р).

Любитель, вероятно, согласится с тем, что это - изящное утверждение (математик назовет его "красивым"). Трудно, однако, ожидать, чтобы любитель представлял себе, насколько неожиданные приложения (например, в небесной механике) имеет эта важная сама по себе теорема. Важность плюс простота (имеется в виду простота результата) ставят теоремы о неподвижных Точках на очень высокое место. Вопросами доказательств, однако, мы еще совсем не занимались. Во-первых, эти доказательства очень нелегко было найти; Пуанкаре, который впервые ввел само понятие неподвижной точки, хотя и сформулировал некоторые теоремы, отдавая себе полный отчет в их перспективной значимости, ничего не доказал. В тоже время доказательства, когда они были найдены, оказались не за пределами понимания любителя (одно из них можно найти в КР).

Является ли теорема о сфере интуитивно очевидной? Я думаю, что ее можно сделать такой. Допустим, что не существует ни одной неподвижной точки (так начинается большинство доказательств). Тогда для каждой точки Р существует (единственная) дуга РР' большого круга сферы, соединяющая точку Р с ее образом Р', причем направление этой дуги (считая от Р) непрерывно изменяется при перемещении точки Р по сфере. (Заметим, между прочим, что здесь мы используем предположение об отсутствии P', диаметрально противоположных Р, иначе дуга РР' не была бы единственной.) Представим себе теперь, что сфера покрыта волосами. Если волос с корнем в точке Р положить вдоль РР', то нам удастся гладко причесать сферу без "особых" точек "раздела" или "встречи": однако мы интуитивно понимаем, что это невозможно. Поэтому должна быть по крайней мере одна особая точка, не снабженная волосом. Вопреки первому впечатлению, нет необходимости в существовании более чем одной такой точки, которая является одновременно и точкой раздела и точкой встречи. На рис. 3 показано, как ложатся волосы около этой точки. Собака, представляющая собой, грубо говоря, топологическую сферу, устроена в этом смысле мало экономно: она имеет целую линию раздела на спине и линию встречи внизу.

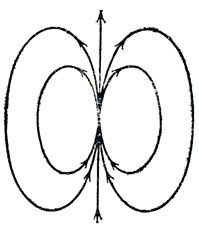
Рис. 3

Каждая выпуклая замкнутая аналитическая поверхность должна иметь по крайней мере две омбилические точки^* (существуют поверхности, имеющие ровно две омбилические точки, причем возможен случай, когда в этих точках R₁ = R₂ = ∞). Эта теорема обладает замечательной особенностью: единственное известное ее доказательство занимает 180 страниц.

^* (Омбилической называется точка, вблизи которой поверхность приближенно сферическая (или плоская): два главных "радиуса кривизны" равны между собой.)

5. Свободный конец нерастяжимой пленки, скатанной в ролик, горизонтально прикреплен к наклонной плоскости и разматывается под действием силы тяжести (рис. 4). Линия соприкосновения всегда имеет скорость нуль, и кинетическая энергия в процессе движения не уничтожается; когда же пленка полностью размоталась, произошла потеря потенциальной энергии, кинетическая же энергия стала равной нулю. Куда девалась энергия?

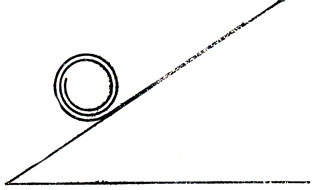
Рис. 4

Аналогичное явление представляет собой хлопок кнута. В "идеальном" кнуте движение кончика завершается воздействием конечной силы на массу, равную нулю, что приводит к бесконечной скорости. Практически же эта скорость превышает скорость звука, и вследствие этого возникает хлопок. Это, быть может, ближайшая реализация бесконечности в повседневной жизни.

Некоторая масса прикреплена к невесомому обручу, который затем катится, оставаясь в вертикальной плоскости, начиная с положения, близкого к положению неустойчивого равновесия. Что произойдет" и можно ли это интуитивно предвидеть?

Обруч подскакивает, когда радиус-вектор массы становится горизонтальным. Я не нахожу отрыв обруча от грунта непосредственно очевидным; можно, однако, "усмотреть", что движение эквивалентно гладкому скольжению массы под действием силы тяжести по циклоиде, которую масса описывает, и тогда уже интуитивно ясно, что рано или поздно масса должна покинуть эту траекторию. (Но указанное "усмотрение" требует понимания того, что мгновенным центром вращения W является Р (рис. 5).)

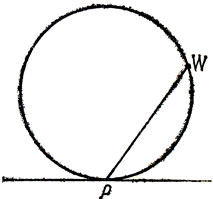
Рис. 5

Г. А. Уэбб ежегодно ставит этот вопрос своим студентам технических факультетов, но я не нашел его в книгах.

Практически обруч сначала скользит.

Предположим, что по некоторому маршруту автобусы ходят приблизительно с десятиминутными интервалами.

"Если бы каждый интервал составлял в точности 10 минут, то среднее время ожидания случайного пассажира, подошедшего к остановке, было бы равно 5 минутам. Если автобусы не вполне точны, то среднее время ожидания больше; существует такое расписание движения, при котором среднее время ожидания равно 10 минутам и более того, при котором среднее время от ухода одного автобуса до прибытия следующего также равно 10 минутам. Существует другое расписание, при котором оба времени становятся бесконечными (долгие ожидания доминируют несмотря на то, что они редки).

Перехожу к следующим двум задачам, похожим друг на друга в том отношении, что первая догадка в каждой из них почти наверное ошибочна (вследствие чего они опасны в недобросовестных руках). Первой могут быть приданы различные формы (одна из таких форм - письма в несоответствующих конвертах); более поздняя форма такая: имеются две хорошо перетасованные колоды карт; в каждой из них открывается верхняя карта, затем открывается пара следующих карт и т. д.; откроются ли когда-либо одновременно одинаковые карты (например, семерки пик)? Результат достаточно широко известен, но большинство из тех, кто его не знает, согласится на большие ставки против этого; в действительности шансы "за" приблизительно равны 17:10 (фактически (e-1):1).

Во второй задаче мы имеем группу в 23 человека; какова вероятность того, что какие-либо 2 из них родились в один и тот же день (год рождения во внимание не принимается)? Большинство считает, что эта вероятность очень невелика, в действительности же она равна примерно ¹/₂.

Рис. 6

Задача Какейя. Найти область наименьшей площади, в которой отрезок единичной длины может непрерывно повернуться на 360й (минимизировать заметенную площадь). Долгое время считалось, что ответ дается рис. 6 и что, следовательно, искомая площадь равна ^π/₈. В 1930 г., однако, А. С. Безикрвич (Besicpvitch A. S. // Math. Z.- 1928.- V. 27.- S. 312-320) показал, что ответом является область нулевой площади (не достижимая): как бы мало ни было данное число ε>0, заметенную площадь можно сделать меньше ε. Когда ε стремится к 0, движения отрезка становятся все более и более сложными и включают путешествия в бесконечность во всех направлениях.

Задача Крама. Каково наибольшее число выпуклых многогранников, каждые 2 из которых имеют общую грань (или часть грани)? Для аналогичной задачи в двух измерениях ответ легко находится: 4; для трех измерений естественно ожидать, что ответом будет 10 или 12. Ответ был найден в 1905 г. Титце и переоткрыт Безиковичем в 1947 г. (J. London Math. Sec.-1947.- V. 22 - P. 285-287). В этой задаче Безикович компенсировал свой предыдущий результат: раньше он нечто уничтожил, а теперь достиг противоположного - ответом является бесконечность.

В одном разговоре недавно возник вопрос: может ли работа в 2 строки быть признана диссертационной? Я давно уже знаю ответ: в математике - да.

*Бесспорным примером является проективное определение длины, данное Кэли, если исходить из разумного понимания слов "2 строчки". Для теоремы Пикара можно придерживаться буквального понимания: одна строка для утверждения, другая-для доказательства.

(Теорема.)

Целая функция, не принимающая значений 0 и 1, постоянна.

(Доказательство.)

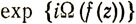  - ограниченная целая функция

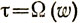[ - функция, обратная к ω = k²(τ)].

Последняя скобка нужна только потому, что обозначение функции Ω в отличие от обратной ей функции k²(τ) не является общепринятым.*

В случае Кэли важность идеи ясна с первого взгляда. В случае Пикара ситуация достаточно ясна сегодня (в связи с теоремой Пикара возникли бесчисленные работы). Но я могу представить себе рецензию оппонента: "Исключительно удачная и весьма оригинальная идея. Но сколь бы она ни была блестяща, она представляется скорее забавной, чем важной; получен изолированный результат, который ни с чем не связан и, скорее всего, никуда не ведет".

*Евклидово доказательство бесконечности множества простых чисел может быть для профессионала сжато в одну строчку:

"Если p₁, p₂, ..., р_n простые, то 1+p₁p₂...p_n не делится ни на одно р_m".

Доказательство Г. Бора того, что "ζ(s) неогреничена для σ>1 для больших t" также может быть сжато в одну строку:

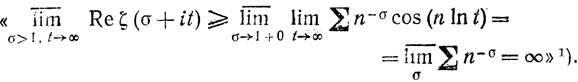
¹⁾ (Предпоследний шаг вынуждает читателя заключить, что здесь используется "теорема Дирихле", и применить соответствующее ее обобщение. [См., например, Титчмарш Е. К.

Дзета-функция Римадо.- М.: ИЛ, 1947.- С. 14-15.- Примеч. пер.))

Моим последним примером является одна сложная теорема высшего анализа. Все же любой математик, признающий важность результата, должен попытаться" не останавливаясь на деталях, усмотреть основную идею ее доказательства^*: эта смелая идея принесла блестящие успехи. Вот эта важная теорема (М. Рисса).

^* (Оно приведено ниже, лемму читатель-математик может про пустить.)

При α, β>0 обозначим М_α,β точную верхнюю грань (т. в. г.) выражения

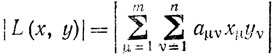
с постоянными комплексными a_μν и переменными комплексными x_μ, y_v, подчиненными условиям

Тогда lnМ_{α, β} является выпуклой функцией α, β (в квадранте α>0, β>0).

Выпуклая функция одной переменной имеет график, для которого (в широком смысле) "дуга лежит под хордой". Выпуклая функция нескольких переменных α, β, ... по определению должна быть выпуклой функцией а на любой прямой l: α = α₀ + λ₁σ, β = β₀ + λ₂σ, ... Для целей приложений теорема формулируется в несколько более общей форме, имеющей иной внешний вид и очень трудно доказуемой, которую для краткости обозначим буквой Г; приведенная формулировка составляет ее основу. В Т область значений аир расширяется путем включения нуля, и тогда теорема позволяет "интерполировать" между двумя известными теоремами, что дает сильный результат. Так, неравенство Юнга - Хаусдорфа для коэффициентов Фурье c_n функции f(θ) из L^p справедливо для 1≤p≤2 (для p = 1 при соответствующей интерпретации^*). Т позволяет нам утверждать, что справедливо общее неравенство, если оно имеет место для p = 1 и р = 2^**. При p = 2 оно сводится к неравенству Бесселя, а при p = 1 (настолько сильна формулировка Т) нам достаточно его знать лишь в приведенной в сноске тривиальной форме. Таким образом, Т дает глубокий результат "из ничего"; мы испытываем нечто похожее на легкое опьянение первых дней метода проектирования конических сечений в окружности.

^* (Именно: "т. в. г. |c_n|≤¹/_2π∫|f|dθ".)

^** (Соответствующая прямая l соединяет точки (¹/₂, ¹/₂) и (1, 0), α = ¹/_p, β = ^p-1_p.)

До последнего времени не существовало доказательства М_{α, β}-теоремы, которое не было бы действительно очень трудным. Приводимое мной доказательство принадлежит Торину (Тhоrin G. Convexity theorems // Communications du seminaire mathematique de l'Universite de Lund.- V. 9).

Мы применяем три непосредственно очевидных принципа:

(a) т. в. г. семейства (возможно, бесконечного) выпуклых функций выпукла,

(b) предел семейства выпуклых функций является выпуклой функцией,

(c) находя т. в. г, чего-либо при ряде независимых условий, наложенных на переменные, мы можем эти условия принимать во внимание в любом порядке (или одновременно); например,

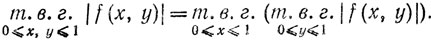
Таким образом, если мы можем представить М_{α, β} в виде

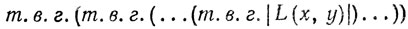
так, что "самая внутренняя" т. в. г. (при фиксированных значениях всех переменных во внешних т. в. г.) выпукла относительно α и β то из (а) и (с) будет вытекать, что наша теорема верна. Торин использует это, беря самую внутреннюю т. в. г. по переменной, которая вообще там не фигурирует!

Начнем с леммы.

Лемма. Предположим, что b₁, b₂, ... b_N действительны и что f(s) является конечной суммой ∑a_re^br^s (или, в более общем виде, целой функцией аргументов e^b₁s, ..., е^b_Ns ), где s = σ + it. Пусть

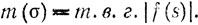
Тогда ln m (σ) - выпуклая функция аргумента σ.

По принципу (b) достаточно доказать это утверждение для случая рациональных b = β'/β. Тогда, если D есть Н. О. К. β, f является целой функцией z = e^sfD. "Теорема о трех окружностях" Адамара, утверждающая, что ln M(r) является выпуклой функцией ln r, дает теперь все, что нам нужно.

Переходим к нашей теореме. Мы должны доказать, что ln M_{α, β} является выпуклой, функцией на любом интервале прямой l: α = α₀ + λ₁σ, β = β₀ + λ₂σ, содержащемся в квадранте α>0, β>0. Для таких α и β мы можем положить

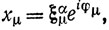
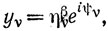
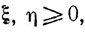
и затем, варьируя (действительные) φ и ψ и (действительные) ξ и η, подчиненные условиям

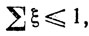
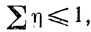
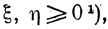
¹⁾ (Эти условия не зависят от α и β.)

получить, что

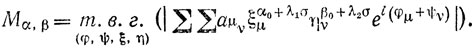
Если мы здесь заменим σ на s = σ + it (с произвольным действительным t), то т. в. г. не изменится (экстремальные φ + ψ будут только "сдвинуты"). Мы теперь можем добавить операцию "т. в. г. относительно t". По принципу (с) мы можем сделать ее самой внутренней; в результате, переходя к логарифмам, находим

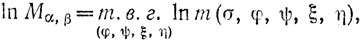
где

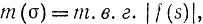
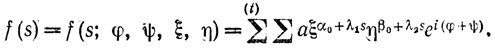
Для интересующего нас участка прямой l (где показатели положительны) и для фиксированных φ, ψ, ξ, η мы можем опустить в сумме f любые члены, в которых ξ или η равно 0; измененное таким образом f имеет вид f из леммы, ln m (σ) является, следовательно, выпуклой функцией для всех σ и, в частности, для, интересующего нас участка прямой по принципу (a). ln M_{α, β} является, таким образом, выпуклой функцией σ.*

6.Шифры. Многие лица, которые должны были бы лучше понимать, о чем идет речь, все еще считают, что любой шифр может быть разгадан. Я приведу достаточный пример, не очень заботясь о степени его осуществимости. Допустим, что мы имеем пятизначное число N. В семизначной таблице логарифмов, начиная со строки N, возьмем последовательность пар последних знаков d₁d₁', d₂d₂', ... Возьмем остаток от деления двузначного числа d_nd_n' на 26. Это дает "сдвиг" s_n; правило кодирования состоит в сдвиге^* первой буквы сообщения на s₁, второй - на s₂, и т. д.

^* (Сдвиг s = 2 переводит "ft" в "т",' "г" - в 'b'. [Английский алфавит имеет 26 букв.- Примеч. пер.])

Совершенно очевидно, что отдельное сообщение не может быть расшифровано, даже если известна система кодирования и тайной является только число N (в действительности втройне случайный характер sn излишне сложен). Один и тот же шифр, применяющийся в ряде сообщений, мог бы быть разгадан, но лишь при неизменном N. Число N можно сделать зависящим от даты, которая сообщается открыто, без зашифровывания; ключ может, например, состоять в том, что N записывается первыми 5 знаками "тангенса" даты (читаемой в градусах, минутах и секундах: 28°12'52" вместо 28-го декабря 1952 г.). Правило можно держать в памяти, чтобы не делать записей, которые могут быть похищены или скопированы. Если кто-либо думает, что существует возможность раскрытия и этого шифра, то он может заменить 28 на 21 и использовать дату, на неделю более раннюю, чем сообщаемая.