Третий этап

В VIII классе продолжается работа по формированию у учащихся понятий вектора и векторной величины. Преемственность этой работы на третьем этапе с предыдущими заключается в параллельном изучении этих понятий, выявлении их взаимосвязи и различий.

Изучение векторных величин в VIII классе на уроках физики основывается на первоначальных представлениях учащихся, полученных в предшествующих классах, и на понятии вектора и его свойств, введенных в курсе геометрии в VII классе.

В процессе изучения векторных величин в VIII классе представления учащихся о векторном характере скорости, силы расширяются, так как подробнее рассматривается их сложение по правилу треугольника, параллелограмма; вводятся новые векторные величины (ускорение, импульс). Такие величины, как момент силы, угловая скорость, которым соответствуют аксиальные векторы, в средней школе не рассматриваются.

Вектор определяет направление векторной величины, а длина вектора равна ее числовому значению в выбранном масштабе. Тот факт, что одни векторные величины могут быть отложены от любой точки плоскости (пространства), другие от любой точки прямой, третьи от фиксированной точки, может быть связан с понятиями свободного вектора (чаще всего им оперируют в математике), скользящего и связанного векторов. Математические знания о векторах находят законное основание для применения в физике.

Все действия с векторами справедливы и для векторных величин, но нужно правильно понимать это утверждение. Например, можно сложить любые векторы. Векторные величины же можно складывать только однородные: силу с силой, скорость со скоростью и т. д., да и то не всегда. Учащиеся дальше узнают, что две силы, приложенные к разным телам, не имеют равнодействующей.

Как и в случае изучения скалярных величин, предлагаемые ниже задания направлены на выявление, закрепление или повторение общих свойств векторных величин, обучение учащихся обращению с величинами. Например, при изучении такой величины, как перемещение, мы предлагаем практическое задание, позволяющее сопоставить эту величину с такой скалярной величиной, как пройденный путь, что помогает понять особенности каждой из рассматриваемых величин.

Задание. Зацепите кончиком карандаша петлю нити и поставьте его в некоторую точку А на листе бумаги. Одной рукой держите вертикально карандаш, а другой - нить у самой петли. Ведите по бумаге карандашом произвольную кривую так, чтобы длина нити за время движения кончика карандаша постоянно увеличивалась. Прекратите движение карандаша и ответьте на вопросы: 1) Что показывает длина вытянутой нити? 2) Чем является длина траектории движения кончика карандаша? 3) Какая из величин больше? 4) Укажите на рисунке направление перемещения. 5) Какова должна быть траектория движения кончика карандаша, чтобы обе величины имели равные числовые значения?

При обсуждении результатов выполнения задания обращаем внимание учащихся на следующее: длина вытянутой линии является модулем (длиной) перемещения; длина траектории есть пройденный кончиком карандаша путь; пройденный путь больше модуля (длины) перемещения; при прямолинейном движении пройденный путь равен модулю (длине) перемещения.

В процессе изучения некоторых величин предлагается несколько заданий. Например, при введении силы учащиеся выполняют три задания: "Наблюдение зависимости результата действия силы на тело от ее значения, направления и точки приложения", "Сложение двух сил, - действующих на одну точку тела под углом друг к другу",

"Наблюдение зависимости сил натяжения нитей от величины угла между ними при постоянной равнодействующей силе". Предлагается в качестве примера первое из заданий.

Используются следующие приборы и материалы: I) брусок деревянный от трибометра; 2) динамометр; 3) нить длиной 200 мм с петлями на концах.

Задание. Положите брусок и динамометр на стол и соедините их нитью. Придерживая брусок левой рукой, отведите динамометр вправо так, чтобы он показывал силу 1 Н (рис. 4, а). Отпустите брусок и наблюдайте за его движением. Повторите опыт при силе натяжения нити 2 Н. Зависит ли результат действия силы на брусок от ее значения? Подействуйте на брусок силой 2 Н, направленной поперек бруска (рис. 4, б). Отпустите брусок и наблюдайте за его движением. Зависит ли результат действия силы на брусок от ее направления? Прикрепите нить к середине бруска. Снова подействуйте на брусок силой 2 И в том же направлении (рис. 4, в). Отпустите брусок и наблюдайте за его движением. Зависит ли результат действия силы на брусок от точки ее приложения?

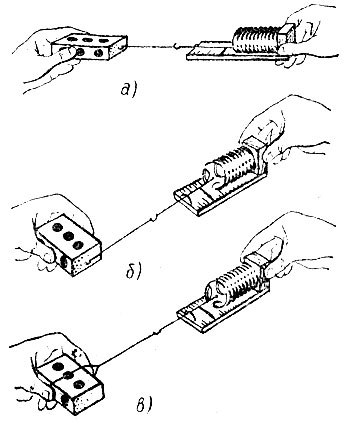
Рис. 4

В ходе опыта учащиеся наблюдают поступательное движение бруска, причем значение действующей силы изменяет его перемещение; при изменении направления действия силы изменяется вид движения бруска (брусок совершает вращательное движение), и, наконец, при изменении точки приложения силы брусок снова совершает поступательное движение.

Таким образом учащиеся убеждаются в том, что результат действия силы зависит от ее значения, направления и точки приложения. Понятие силы как векторной величины развивается и дальше в процессе изучения конкретных видов сил: силы тяжести, силы упругости, силы трения.

После изучения понятия о силе обобщаем свойства векторных величин:

1. Векторная величина характеризуется направлением в пространстве и размером (при выбранной единице измерения - числовым значением).

2. Для векторных величин устанавливаются операции сложения, умножения на число и скалярную величину. Складывать можно только однородные величины. В результате умножения векторной величины на число получаем векторную величину того же рода и того же или противоположного направления. В результате умножения векторной величины на положительную скалярную получают векторную величину другого смысла, но сонаправленную с данной.

3. Каждой векторной величине ставится в соответствие вектор (свободный, скользящий или связанный). Это соответствие устанавливается через операцию откладывания векторной величины в виде направленного отрезка как вектора.

4. Операции сложения и умножения на число обладают свойствами, аналогичными свойствам векторов.

5. Понятия вектора, векторной величины взаимосвязаны, но не тождественны.

6. При выбранной единице измерения имеем взаимно-однозначное отображение множества векторных величин на множество чисел.

7. Множество, составленное из множеств различной природы (сил, ускорений и т. д.), образует систему разнородных векторных величин.