Первый этап

Учащиеся на уроках математики знакомятся с понятиями направления на прямой, плоскости, с отрицательными числами и действиями над ними, координатной прямой и плоскостью, параллельным переносом фигуры и др. Использование этих понятий позволяет в VI классе на уроках физики преодолеть существенную трудность при первоначальном знакомстве с векторными величинами, так как понятие вектора вводится позднее, в VII классе. Так, при изучении темы "Направления и числа" в V классе вводим понятие направленного отрезка как отрезка со стрелкой на конце; говорим, что направленным отрезком можно характеризовать положение предмета (тела). В тетради учащиеся изображают горизонтальную прямую и отмечают на ней произвольную точку О. Предлагаем отметить точку А, которая находится в 3 см от точки О. Подводим учащихся к пониманию неоднозначности задания: точку можно отметить , как слева от точки О, так и справа. Чтобы отметить точку А, недостаточно знать расстояние |ОА|. Надо еще знать направление отсчета расстояния. Уточняем задание: отметить точку А слева от точки О. Говорим, что положение точки А по отношению к точке О можно характеризовать отрезком ОА со стрелкой на конце (направленным отрезком). Далее учащиеся выполняют задания, в которых по известному положению предмета (точки) строят направленный отрезок, задающий это положение, и, наоборот, по направленному отрезку определяют положение предмета (точки).

Учащиеся выполняют ряд заданий, аналогичных приведенным в учебнике, только каждый раз отмечая положение точки (предмета) направленным отрезком.

После ознакомления учащихся с координатной прямой выполняют задание, где с помощью положительных и отрицательных чисел обозначают не только положение точек на ней, но и перемещения точек по этой прямой.

Уже в V классе на уроках математики учащиеся выполняют параллельный перенос геометрической фигуры в заданном направлении на заданное расстояние, причем это перемещение задается не столько парой точек, сколько направленным отрезком. В VI классе на уроках физики в теме "Движение и силы" показываем учащимся связь параллельного переноса с движением тел, подчеркнув, что результат движения (как и параллельного переноса) может быть охарактеризован указанием не только расстояния, но и направления. Удобнее всего это сделать на примере такой величины, как перемещение. Векторный характер перемещения понятен учащимся, так как ближе к их жизненным представлениям, чем векторный характер скорости и силы. Тем более что учебный материал по математике V класса, рассмотренный выше, вплотную подготавливает учащихся к введению перемещения как векторной физической величины. На примере перемещения могут быть раскрыты свойства, присущие большинству векторных величин.

Пропедевтическое изучение понятия перемещения в VI классе способствует более осознанному пониманию векторного характера скорости и силы.

Кроме того, первоначальное введение перемещения позволяет сопоставить его с такими скалярными величинами, как пройденный путь и расстояние. Это помогает сразу выделить те особенности векторных величин, которые отличают их от скалярных.

Если тело движется прямолинейно, то направление движения можно задать на координатной прямой (о том, как задается координатная прямая, о положительном и отрицательном направлениях, о понятии координаты точки они знают из курса математики V класса). Тело может перемещаться в двух направлениях: вправо или влево. Начало движения (наблюдения) всегда можно связать с началом отсчета.

Пусть какая-либо точка тела (рис. 3) начала двигаться вправо из положения О с координатой, равной нулю. Через некоторое время точка займет новое положение А с координатой, равной 3. Если тело движется так, что траектории всех его точек одинаковы, то любая из этих точек переместится в том же направлении на то же расстояние. Имеем дело с параллельным переносом всех точек тела в направлении от точки О к точке А на расстояние, равное 3 м. Начальное и конечное положения какой-либо точки задают параллельный перенос.

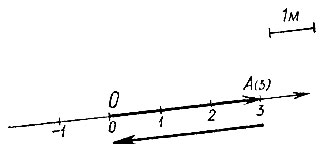
Рис. 3

Длина отрезка О А характеризует значение перемещения тела. Указав направление перемещения стрелкой у точки А, получим направленный отрезок, который наряду с парой точек (О; А) задает параллельный перенос любой точки тела. Одновременно направленный отрезок О А характеризует изменение положения точки. Таким образом, результат движения может быть охарактеризован не только расстоянием, но и направлением.

Обращаем внимание учащихся на различие понятий "перемещение" и "расстояние". Перемещение является направленной величиной. Модуль перемещения является расстоянием^*. Расстояние - величина, не имеющая направления.

^* (В курсе геометрии VI класса вводится аксиоматическое определение понятия расстояния как неотрицательной скалярной величины. Здесь даем "физическую" интерпретацию этого понятия, не противоречащую принятой в курсе геометрии)

Длину траектории, по которой проходит точка за некоторый промежуток времени, называют пройденным путем.

Если рассматривать движение точки из положения О в положение А и обратно, то учащимся ясно, что результирующее числовое значение перемещения равно нулю (нулю равно и расстояние), а путь равен 6 м.

Важно, чтобы ученики понимали различие между значением перемещения и пройденным путем: числовое значение результирующего перемещения зависит от направления движения, тогда как путь от направления не зависит. Путь принимает только неотрицательные значения.

Далее рассматриваем пример, иллюстрирующий векторное сложение перемещений.

Произвольно направленными отрезками задаем два последовательных перемещения тела и находим (построением) его результирующее перемещение. Используя известные свойства расстояний, учащиеся делают вывод, что сумма двух последовательных значений перемещения больше значения результирующего перемещения. Подчеркиваем, что алгебраическое сложение значений величин в этом случае неприменимо.

Приведем примеры таких задач, вопросов и практических заданий, которые можно использовать на уроках физики в VI классе и на уроках математики в VII классе при изучении векторов.

1. Турист проходит расстояние между двумя городами, равное 25 км. Может ли путь, пройденный туристом, быть больше этого расстояния? В каком случае путь равен расстоянию? Результат движения туриста изобразите направленным отрезком.

2. Ящик по полу переместили влево на 3 м. Изобразите на рисунке новое положение ящика. Все ли точки ящика переместились на данное расстояние? Можно ли назвать его перемещение параллельным переносом? Задайте это перемещение направленным отрезком.

3. Велосипедист проезжает сначала в направлении на север o 20 км, потом на восток 10 км. Каков пройденный путь велосипедиста? Что больше: пройденный путь или расстояние между начальным и конечным положением велосипедиста? В каком же месте окажется велосипедист, если сначала он пройдет на восток 10 км, потом на север 20 км?

4. Точка, координата которой равна 2, переместилась в положение с координатой - 3. Сделайте чертеж и найдите значение и направление перемещения. Изобразите перемещение направленным отрезком .в масштабе: в 1 см 2 м.

5. Кончик карандаша переместился по прямой линии вертикально вниз. Каково должно быть перемещение кончика карандаша, чтобы результирующее перемещение было равно нулю?

6. Отметьте на листе бумаги точку А и проведите произвольный отрезок. Укажите направление перемещения кончика карандаша. Измерьте длину отрезка. Совершите такое движение карандаша, чтобы результирующее перемещение было равно нулю.

Такого типа задания показывают связь параллельного переноса в математике с движением тел в физике, причем связующим понятием является понятие направленного отрезка, с помощью которого задается и параллельный перенос, и результат движения за некоторый промежуток времени. Учащимся сообщается, что, построив направленный отрезок, мы задали (или отложили) параллельный перенос.

При изучении скорости и силы обращается внимание учащихся на направленный характер этих величин. Значения скорости и силы можно задавать длиной отрезка в заранее выбранном масштабе.

Для понимания этого материала учащимся можно предложить следующие задания:

1. Два велосипедиста движутся прямолинейно навстречу друг другу со скоростью 10 м/с. Чем отличаются скорости велосипедистов? Выбрав масштаб, изобразите скорости направленными отрезками.

2. Автомобиль проехал по прямой дороге 90 км за 1,5 ч. Изобразите перемещение и скорость автомобиля направленными отрезками. Чем отличаются эти отрезки и в чем сходство?

3. На крючок динамометра подвесили груз массой 300 г. Вычислите и изобразите силу тяжести и силу упругости, действующие на груз и его вес.

4. Две силы действуют на покоящееся тело. При каких условиях тело может оставаться в покое? Изобразите эти силы.

Можно также предложить учащимся практические задания, в которых требуется измерить величины, определить их направление, ответить на некоторые вопросы, требующие понимания их направленного характера, выполнить действия со значением этих величин. Например, при изучении скорости равномерного движения по прямой предлагаем учащимся выполнить задание, которое знакомит их с направленным характером скорости, показывает связь направления скорости с направлением перемещения. Учащиеся наблюдают за движением стеаринового или пластилинового шарика в стеклянной трубке с водой при двух ее положениях: вертикальном и наклонном - и отвечают на вопросы: 1) как направлено перемещение шарика в каждом случае; 2) как направлена скорость шарика в каждом случае; 3) какой вывод можно сделать о связи направления скорости с направлением перемещения. Затем они схематически изображают перемещение и скорость на рисунках.

При изучении силы можно предложить задания, которые раскрывали бы ее общие свойства: сила имеет точку приложения, направление и размер, точку приложения силы можно перемещать вдоль линии ее действия; силы складываются иначе, чем положительные скалярные величины. Выполняя задания, учащиеся измеряли силы, устанавливали связи с другими величинами. Например, при измерении силы, необходимой для равномерного движения бруска трибометра с грузом по столу, проверяется: изменится ли числовое значение силы, ее направление, а также ее действие, если между бруском и динамометром поместить нить (предложить нити разной длины)? На основе наблюдений, измерений учащиеся делают выводы. Затем откладывают силу на прямой в виде направленного отрезка. Точка приложения силы выбирается произвольно на данной прямой (в дальнейшем учащимся сообщаем, что точку приложения силы для удобства фиксируют).

При знакомстве учащихся со сложением двух сил, направленных по одной прямой, можно предложить следующее задание.

Задание. Подвесить к крючку динамометра груз массой 100 г. Каков вес груза? Отложите его от точки подвеса. Подвесить к первому грузу второй такой же груз. Изобразить вес второго груза, отложив его от конца первого направленного отрезка. Чему равна равнодействующая сила? Изобразить ее на рисунке. Подействовать слегка на крючок динамометра рукой вертикально вверх и записать показание динамометра. Вычислить силу, с которой рука действовала на крючок динамометра. Изобразить силы графически. Подействовать на крючок динамометра вертикально вверх так, чтобы указатель динамометра установился на нулевом делении шкалы. Чему равна сила, с которой рука действовала вверх на крючок динамометра? Каково ее направление? Изобразить силы графически.

При выполнении задания учащиеся сначала складывают две равные силы, затем складывают противоположно направленные силы и, наконец, убеждаются в том, что равнодействующая двух равных по модулю и противоположно направленных сил равна нулю.

В заключение покажем пример задания, в процессе выполнения которого учащиеся знакомятся с операцией вычитания двух сил, направленных по одной прямой.

Задание. Подвесить к крючку динамометра груз массой 100 г. Чему равно значение и направление силы тяжести, действующей на этот груз? Подвесить к крючку груза металлический цилиндр. Чему равна сила тяжести, действующая на груз и цилиндр вместе? Изобразить обе силы направленными отрезками и определить графически силу тяжести, действующую только на цилиндр. Проверить свой ответ, подвесив к динамометру .только цилиндр.

Задание знакомит учащихся с операцией вычитания сил как векторных величин. Оно помогает понять, что вычитание по существу операция, обратная сложению.