§ 10. Измерения при различных ограничениях

Для нахождения расстояний, высот, глубин или других размеров реальных объектов не всегда можно обойтись непосредственным их измерением - во многих случаях такие измерения сопряжены с определенными трудностями, а то и вообще практически невозможны. Однако в своей деятельности человеку приходится порой задумываться над тем, как все-таки можно определить интересующую его величину и как сделать это поточнее.

Вероятно, каждый из вас не раз задавал сам себе вопросы подобного рода, но вряд ли сходу находил на них ответы. В настоящем параграфе вам предлагается подумать над некоторыми наиболее типичными задачами. Советуем при их решении побеспокоиться о том, чтобы предлагаемый вами способ был действительно осуществим на практике и использовал минимум необходимых средств для построений (см. § 9), измерений и вычислений. Дело в том, что основными измерительными "приборами" для вас, которые всегда имеются "под рукой", будут являться: шаг, пядь (размах пальцев), сажень (размах рук), уровень глаз (расстояние от земли до глаз) и т. д. Не менее важно следить за надежностью вашего способа, т. е. зависимостью его точности от различных погрешностей, которые неизбежно возникают при работе на местности.

Вы хотите определить длину своего шага, чтобы впоследствии измерять расстояния шагами. Самый простой и, казалось бы, точный способ состоит в том, чтобы сделать один шаг и измерить расстояние между крайними (наиболее удаленными) точками двух ступней. Такой способ явно не годится по двум причинам. Во-первых, расстояние между крайними точками ступней не равно длине шага, а превосходит ее на длину одной ступни (правильнее было бы измерить расстояние, например, между носками двух ступней). Во-вторых, при всем старании вы вряд ли сможете сделать один обычный шаг - для этого вам нужно оказаться в состоянии обычной ходьбы. Так, как же все-таки определить длину своего шага?

Измеряя какие-либо длины пальцами руки, лучше не отрывать руку от измеряемой поверхности, а приставлять один палец к другому, который затем снова вытягивать в заданном направлении (описанный процесс отдаленно напоминает движение гусеницы). Найдите длину такого размаха своих пальцев.

Как по длине тени, падающей от дерева в солнечный день, определить высоту этого дерева?

В вашем городе установлен большой памятник. К вам в руки попала почтовая карточка с фотографией этого памятника, сделанной с почтительного расстояния от него. Можно ли воспользоваться этим снимком для определения высоты памятника?

Вам понадобилось измерить на местности расстояние между двумя объектами, разделенными зданием или другим препятствием, не позволяющим непосредственно проложить прямую между этими объектами. Как тем не менее можно произвести указанное измерение?

Вы плывете на лодке по озеру и хотите узнать его глубину. Нельзя ли воспользоваться для этого торчащим из воды камышом, не вырывая его?

Укажите способ, как измерить высоту дерева, не взбираясь на него и не прибегая к помощи теней.

Перед вами раскинулся огромный пруд круглой формы, обойти который по окружности вы не можете из-за имеющихся на его берегу различных препятствий в нескольких местах. Кроме того, вам представляется затруднительным измерять расстояние между какими-либо точками, если только соединяющий их отрезок проходит над водой. Можно ли при таких ограничениях измерить диаметр пруда?

Вы хотите узнать, на какой высоте находится шпиль, расположенный на здании, внутри и вблизи которого измерения затруднительны. Как, не приближаясь к зданию вплотную, измерить высоту шпиля?

Стоя на краю обрыва, вы хотите измерить глубину находящегося перед вами котлована. Нельзя ли это сделать, не спуская с обрыва никаких веревок?

Вы находитесь на берегу реки и хотите измерить ее ширину, не имея возможности перебраться> на другой берег. Для этого вы отыскиваете глазами на противоположном берегу реки близко к воде какой-либо заметный ориентир А - камень, деревце и т. п.- и отмечаете на своем берегу точку В, расстояние от которой до точки А представляет собой, по-вашему, ширину реки. Как измерить длину отрезка АВ?

Вы хотите узнать расстояние до высокого здания, которое можно увидеть прямо со двора вашего дома. Естественно, в городских условиях непосредственно пройти к зданию по прямой линии вам не удастся. Более того, свои геометрические построения вы можете осуществлять лишь на сравнительно небольшой площадке перед домом. Укажите способ для определения искомого расстояния.

Вы находитесь на одном берегу реки, а на другом, недоступном для вас берегу расположены два объекта. Как вас берегу расположены два объекта. Как измерить расстояние между ними?

Решения

10.1. Достаточно пройти какое-либо заранее известное и не слишком короткое расстояние, скажем между соседними километровыми или стометровыми столбиками на шоссе, и поделить это расстояние на количество сделанных шагов.

Отметим, что средняя длина шага взрослого человека примерно равна половине его роста, считая до уровня глаз.

10.2. Проще всего отложить вдоль какой-нибудь прямой один или несколько десятков размахов пальцев, а затем поделить на их количество отложенную в результате длину.

10.3. Так как лучи солнца можно считать практически параллельными, то тень от дерева во столько же раз длиннее тени от какого-либо шеста, во сколько раз дерево выше шеста. Поэтому, установив вертикально шест известной высоты а и измерив отношение k длины тени от дерева к длине тени от шеста, мы вычислим искомую высоту дерева ka.

Заметим, что указанный способ не слишком надежен, так как отбрасываемая при свете солнца тень не имеет отчетливой границы из-за присущей ей неясно очерченной каймы полутени.

10.4. Для приблизительного нахождения высоты памятника по снимку можно выбрать две точки, расположенные у фундамента этого памятника, и измерить расстояние между ними на фотографии и на местности (второе расстояние нас интересует скорее не в чистом виде, а как проекция на прямую, перпендикулярную направлению, в котором был сфотографирован памятник). Найдя отношение k первого из расстояний ко второму, мы узнаем масштаб снимка, после чего останется замерить на нем высоту памятника и поделить ее на k.

10.5. Пусть А и В - данные точки на местности, между которыми определяется расстояние. Выберем точку С, из которой видны обе точки А я В (рис. 13). На продолжении отрезка АС за точку С отметим точку D на расстоянии АС от точки С. Аналогично на продолжении отрезка ВС за точку С отметим точку Е, для которой СЕ = ВС. Тогда отрезки ED и АВ равны, поскольку они симметричны относительно точки С.

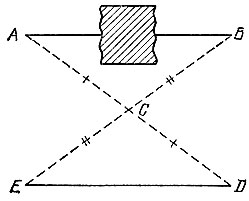
Рис. 13

Если же из-за недостатка места точки Е и D выйдут за пределы досягаемости, то их можно в определенное число раз приблизить к точке С. Тогда отрезок ED будет в то же число раз короче отрезка АВ, так как треугольники ABC и DEC будут подобны.

10.6. Слегка отклонив камыш и держа его в натянутом состоянии, замерим расстояние а между точками А и В, в которых камыш пересекает поверхность воды соответственно в вертикальном и наклоненном положении (рис. 14). Возвратим камыш в исходное состояние и определим высоту b над водой, на которую поднимется при этом точка В наклоненного камыша, заняв исходное положение С. Тогда, обозначив через D основание камыша, а через х - искомую глубину AD, из прямоугольного треугольника ABD находим

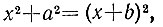
откуда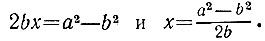

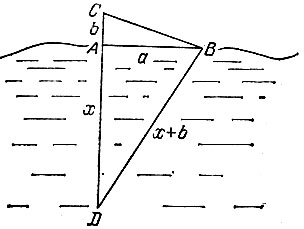
Рис. 14

10.7. Установив вертикальный шест на некотором расстоянии от дерева, нужно стать в такую точку, из которой верхний конец шеста загораживает в точности верхушку дерева (рис. 15). Тогда, если высота части шеста над уровнем глаз равна а, а расстояния от глаз по горизонтали до шеста и до дерева равны b и y соответственно, то из подобия треугольников можно найти высоту х дерева над уровнем глаз. Наконец, зная свой рост h до уровня глаз, получаем полную высоту дерева

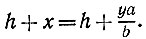
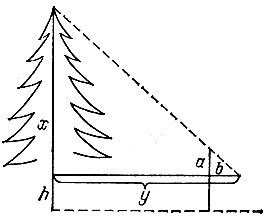
Рис. 15

Заметим, что вычисления и измерения можно упростить, если добиться равенства b = a, которое достигается выбором места установки шеста. Кроме того, можно лечь на землю, что позволит считать h = 0, а в результате высота дерева окажется равной x = y.

10.8. Встав в точку А на некотором расстоянии от пруда (рис. 16), можно расположить перед собой горизонтальную палку длины а так, чтобы расстояния от обоих ее концов до одного глаза (второй глаз при этом лучше закрыть) были равны одному и тому же значению b, а сами концы палки зрительно совместились с крайними точками пруда, видимыми из точки А. Тогда, измерив расстояние у от А до ближайшей точки пруда по прямой, проходящей через середину палки, можно вычислить радиус х пруда, а значит, и его диаметр 2х. Действительно, из подобия соответствующих прямоугольных треугольников находим

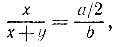
откуда 2bx = ах + аy, т. е. 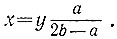Заметим, что если добиться равенства b = а (что достигается выбором точки A), то коэффициент при y в последней формуле будет равен 1, а искомый диаметр пруда окажется равным 2x = 2y.

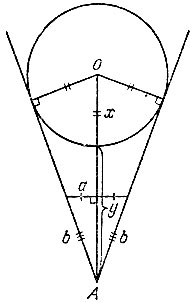
Рис. 16

10.9. Установим вертикальный шест на некотором расстоянии от здания и станем в такую точку, из которой верхушка шпиля зрительно совмещается с верхним концом шеста (рис. 17). Затем, пройдя некоторое расстояние в направлении от здания по прямой, на которой лежит первая точка и проекция А шпиля на горизонтальную плоскость, еще раз проделайте такую же операцию. Пусть высота шеста над уровнем глаз равна а, расстояние от глаз до шеста в первом положении оказалось равным b, а во втором с. Тогда, измерив расстояние у между точками В и С, в которых мы стояли в первом и во втором случаях, можно сосчитать высоту х шпиля над уровнем глаз. В самом деле, обозначим через z расстояние между точками А и В. Из подобия соответствующих треугольников имеем

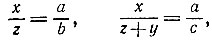
откуда bx = az, cx = az + ay и cx - bx = ay, т. е.

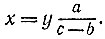
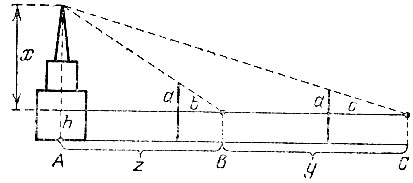
Рис. 17

Коэффициент при y в последнем равенстве можно сделать равным 1, если в первом положении шеста добиться равенства b = а, а во втором - равенства с = 2а.

10.10. Глубину котлована можно измерить с помощью короткой палки. Для этого достаточно отыскать глазами на дне котлована какой-либо ориентир О и, встав на краю обрыва, установить палку горизонтально так, чтобы основание В палки оказалось на одной вертикали с глазами H, а другой ее конец А зрительно совместился с ориентиром О (рис. 18). Такую же операцию нужно проделать, лежа на краю обрыва и опустив основание С палки по той же вертикали ниже края обрыва. Измерив расстояния b и c от глаз до основания палки в первом и во втором положении соответственно, а также зная свой рост h до уровня глаз, можно вычислить глубину х котлована. Действительно, обозначим через y расстояние по горизонтали от ориентира до проекции края обрыва. Тогда из подобия соответствующих треугольников имеем

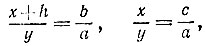
откуда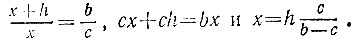

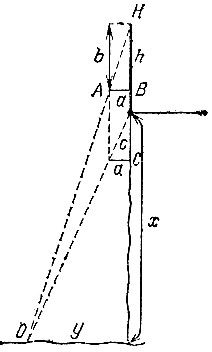
Рис. 18

10.11. Выберем точку С на продолжении прямой АВ за точку В, а также точку D, не лежащую на прямой АВ (рис. 19). Затем выберем точки Е и F на продолжениях прямых BD и CD соответственно за точку D так, чтобы выполнялись равенства BD = DE, CD = DF. Наконец, найдем точку G пересечения прямых EF и AD. Тогда искомое расстояние между точками А а В будет равно длине отрезка EG. Действительно, из равенства треугольников BDC и EDF (по двум сторонам и углу между ними) имеем равенство углов CBD и FED. Поэтому треугольники BAD и EGD равны (по стороне и двум прилежащим к ней углам), а значит, равны и их соответствующие стороны АВ и GE.

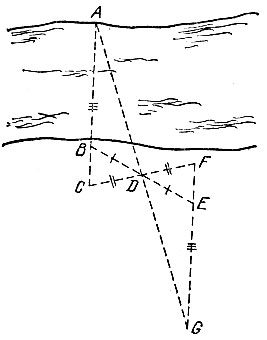
Рис. 19

10.12. Для нахождения расстояния от данной точки В до недоступной точки А можно использовать построения, аналогичные приведенным в решении задачи 10.11 с той лишь разницей, что точки Е и F на рис. 19 следует выбрать ближе к точке D, т. е. на расстоянии, в одинаковое число раз меньшем длин отрезков BD и CD соответственно. Во столько же раз отрезок GE окажется меньшим отрезка АВ, что вытекает из подобия (а не равенства, как это было в решении задачи 10.11) треугольников BAD и EGD.

10.13. Путь А и В - недоступные точки, между которыми надо найти расстояние. Выберем на некоторой прямой три точки D, Е и F так, чтобы выполнялось равенство DE = EF (рис. 20). При этом заранее побеспокоимся о том, чтобы точка С пересечения прямых AF и BD оказалась доступной и лежала с той же стороны от прямой DF, что и отрезок АВ: этого можно достичь уменьшением отрезка DF и переобозначением его концов. На продолжении отрезка СЕ за точку Е отметим точку G на расстоянии СЕ от точки Е. Далее найдем точку Н пересечения прямых DG и АЕУ а также точку К пересечения прямых FG и BE. Тогда искомое расстояние будет равно КН. Действительно, при преобразовании симметрии относительно центра Е точка С переходит в точку G, точка D - в точку F, прямая CD - в прямую GF, прямая BE - в себя, а точка В пересечения прямых CD и BE - в точку К пересечения GF и BE. Аналогично точка Л при этом преобразовании переходит в точку H, поэтому отрезок НК симметричен отрезку АВ относительно точки Е.

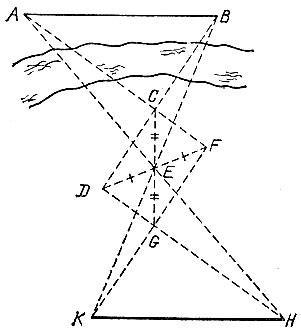
Рис. 20