§ 9. Простейшая геометрия на местности

Для практических целей часто возникает необходимость производить геометрические построения на местности. Такие построения нужны и при строительстве зданий, при прокладке дорог, и при различных измерениях объектов на местности. Можно подумать, что работа на ровной поверхности земли (а именно такой мы и будем ее считать во всех задачах настоящего параграфа) ничем, по существу, не отличается от работы циркулем и линейкой на обыкновенном листе бумаги. Это не совсем так. Ведь на бумаге циркулем мы можем проводить любые окружности или их дуги, а линейкой - любые прямые. На местности же, где расстояния между точками довольно велики, для подобных действий понадобилась бы длинная веревка или огромная линейка, которые не всегда имеются под руками. Да и вообще чертить прямо на земле какие бы то ни было линии - дуги или прямые - представляется весьма затруднительным. Таким образом, построения на местности имеют свою специфику.

Во-первых, откажемся от проведения настоящих прямых на земле. Будем эти прямые прокладывать, т. е. отмечать на них, например, колышками, достаточно густую сеть точек. Для практических нужд этого обычно хватает, поскольку передвижение по прямой от одного колышка к другому, расположенному на близком расстоянии от первого,- действие, вполне осуществимое.

Во-вторых, запретим при построениях проводить на земле какие-либо дуги вообще - большие или маленькие. Поэтому фактически циркуля у нас нет. Все, что остается от циркуля,- это способность откладывать на данных (проложенных) прямых конкретные расстояния, которые должны быть заданы не численно, а с помощью двух точек, уже обозначенных колышками где-то на местности. Ведь сами расстояния будут измеряться шагами, ступнями, пальцами рук или любыми подходящими для этой цели предметами (в лучшем случае измерительными приборами). Так что отложить расстояние, составленное, скажем, из 25 шагов, 3 размахов пальцев и 2 спичечных коробок, можно лишь в таком же виде, но никак не умноженное, к примеру, на ³/₄ или на √2.

При указанных двух ограничениях, не пользуясь к тому же транспортиром, работать, конечно, трудно, но все же попробуйте решить предложенные ниже задачи!

На местности колышками обозначены две удаленные друг от друга точки. Как проложить через них прямую и, в частности, как можно без помощника устанавливать колышки на прямой между данными точками?

На местности колышками обозначены две точки одной прямой и две точки другой прямой. Как найти точку пересечения этих прямых?

На местности обозначены точки A и В. Найдите точку С, симметричную точке A относительно точки В.

На местности обозначены три данные точки A, В и С, не лежащие на одной прямой. Через точку A проложите прямую, параллельную прямой ВС.

Найдите середину отрезка AВ, заданного на местности двумя точками A и В.

Отрезок, заданный на местности двумя точками A и В, требуется разделить в отношении, в котором находятся длины двух отрезков KL и MN, заданных на местности точками К, L и М, N. Как это сделать?

На местности обозначены три точки A, М и N, не лежащие на одной прямой. Проложите биссектрису угла MAN.

Проложите на местности какую-нибудь прямую, перпендикулярную прямой, проходящей через заданные точки A и В. Как проложить перпендикуляр к прямой АВ, проходящий через данную точку Я?

На местности обозначены точки A и В. Найдите точки С, D и В, для которых выполнены равенства ∠ ВAС = 45°, ∠ BAD = 60° ∠ ВAE = 30°.

Решения

9.1. Пользуясь зрительным эффектом состоящим в загораживании двух колышков третьим, стоящим на общей с ними прямой, нетрудно установить еще один колышек в некоторой точке С на продолжении отрезка с концами в двух данных точках A и В. После этого точки отрезка АВ можно построить с помощью того же эффекта, поскольку они будут лежать на продолжении либо отрезка АС, либо ВС (в зависимости от того, какая из точек - А или В - находится ближе к точке С). Вообще, любая точка прямой АВ будет лежать на продолжении хотя бы одного из отрезков АВ, АС или ВС.

9.2. Пользуясь зрительным эффектом, указанным в решении задачи 9.1, легко найти точку пересечения прямых в том случае, если сразу ясно, что она лежит на продолжениях своих отрезков с концами в данных точках. В противном случае достаточно сначала проложить одну или обе прямые так, чтобы на каждой из них с одной стороны от предполагаемой точки пересечения были отмечены по две точки.

9.3. Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится измерить в подходящих единицах длины расстояние между точками А и В.

9.4. Продолжим прямую АВ за точку В и отложим на ней точку D на расстоянии АВ от точки В (рис. 8). Продолжим прямую CD за точку С и отложим на ней точку Е на расстоянии CD от точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника ADE. Заметим, что предложенный способ выгодно отличается от множества других способов, опирающихся на измерение углов или на деление отрезка пополам.

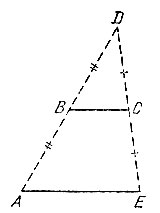
Рис. 8

9.5. Возьмем какую-либо точку С, не лежащую на прямой АВ. Продолжим прямую ВС за точку С и отложим на ней точку D на расстоянии 2ВС от точки С (рис. 9). Продолжим прямую AD за точку А и отложим на ней точку Е на расстоянии AD от точки А. Искомая середина F отрезка АВ лежит на его пересечении с прямой ЕС. Действительно, отрезок СЕ параллелен отрезку AG - средней линии треугольника CDE (здесь G - середина отрезка CD). Так как, кроме того, BC = CG, то CF - средняя линия треугольника ABG, откуда AF = FB.

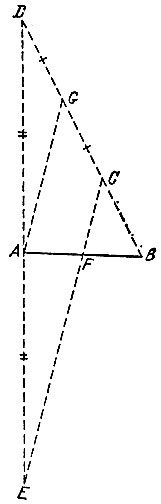
Рис. 9

Быть может, приведенный способ нахождения середины отрезка покажется вам не самым простым. Однако его преимущества хорошо проявляются в следующей задаче, решив которую вы сможете делить отрезок не только на две, но и на любое число равных частей.

9.6. Построение точки F, делящей отрезок А В в отношении AF:BF = KL:MN, произведем аналогично построению середины отрезка АВ, описанному в решении задачи 9.5. Отличие будет состоять только в том, что точку С выберем на расстоянии KL от точки В, а точку D - на расстоянии 2MN от точки С (рис. 9). В этом случае прямая ЕС по-прежнему будет параллельна отрезку AG, а значит, разделит отрезок АВ в том же отношении, в котором она делит отрезок BG.

9.7. Выберем на одной стороне данного угла (рис. 10) точки В и С, а на другой - точки D и Е так, чтобы выполнялись равенства

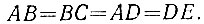
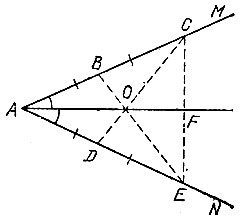
Рис. 10

Найдем точку О пересечения прямых BE и CD. Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике АСЕ биссектриса AF является одновременно и медианой, а значит, проходит через точку О пересечения медиан ЕВ и CD.

9.8. Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Кроме того, отложим на том же расстоянии от точки В еще две точки D и Е в двух разных, но не противоположных направлениях (рис. 11). Найдем точку F пересечения прямых АЕ и CD, а также точку G пересечения прямых AD и СЕ.

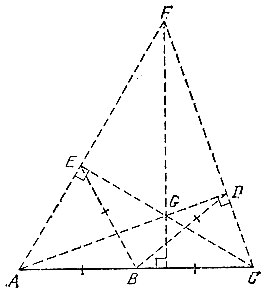
Рис. 11

Прямая FG перпендикулярна прямой АВ. Действительно, точки А, Е, D и С равноудалены от точки В, т. е. лежат на одной окружности с центром В и диаметром АС. Следовательно, вписанные углы ADC и АЕС прямые, поэтому AD и СЕ - высоты треугольника AFC. Так как все три высоты этого треугольника пересекаются в одной точке G, то прямая FG перпендикулярна стороне АС. Для того чтобы проложить перпендикуляр к прямой АВ через данную точку Я, достаточно теперь проложить через эту точку прямую, параллельную прямой FG (см. задачу 9.4).

9.9. Проложим перпендикуляр к прямой АВ (см. задачу 9.8), пересекающий в какой-то точке луч АВ. Без ограничения общности считаем для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложим точки С и F (рис. 12), удаленные от точки В на расстояние АВ. Тогда угол ВАС равен 45° (из равнобедренного прямоугольного треугольника ABC). На прямой AF отложим точку G на расстоянии АВ от точки А, а затем на прямой ВС отложим точку D на расстоянии CG от точки В. Тогда угол BAD равен 60Q, так как по теореме Пифагора для прямоугольных треугольников ABC, ACG и ABD имеют место равенства

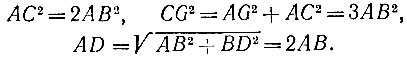
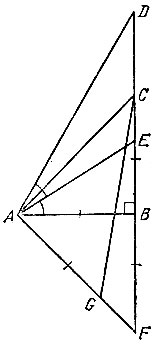
Рис. 12

Для построения точки Е теперь остается проложить биссектрису угла BAD (см. задачу 9.7).