
§ 5. Вокруг наибольшего общего делителя

Одна из простейших задач, для решения некоторой понадобится найти наибольший общий делитель пары натуральных чисел а и b,- это 1 задача сокращения дроби a/b. Напомним, что если числа а и b делятся на одно и то же натуральное число d, то число d называется общим делителем пары чисел а и b. Любая пара натуральных чисел имеет хотя бы один общий делитель (а именно, d = 1), причем любой общий делитель не превосходит каждого из этих чисел. Поэтому среди всех делителей чисел а и b можно выбрать наибольший общий делитель, который обозначается через (а, b), например (20, 100) = 20, (65, 39) = 13. Если (а, b) = 1, то числа а и b называются взаимно простыми. При этом взаимно простые числа а и b совсем не обязательно сами по себе должны быть простыми числами; так, (33, 35) = 1, но 33 = 3*11 и 35 = 5*7.
У читателя, возможно, сложилось впечатление, что нахождение наибольшего общего делителя пары чисел представляет собой очень простую задачу. Ведь если разложить на простые множители каждое из данных чисел, то сразу станет ясно, как составить из этих простых множителей наибольшее произведение, на которое делятся оба данных числа. Однако все дело в том, что разложить число на простые множители иногда бывает довольно трудно, тогда как нахождение наибольшего общего делителя можно осуществить намного проще - с помощью несложной процедуры. Эта процедура известна уже более 2 тысяч лет и носит название алгоритма Евклида.
Алгоритм Евклида применяется ко многим с виду разнородным объектам. Нахождение наибольшего общего делителя, разложение дроби в цепную дробь, приближение дроби более простыми, решение уравнений в целых числах - вот далеко не полный перечень приложений этого алгоритма, с которыми вы познакомитесь в настоящем и следующем параграфах.
5.1. Разлагая на множители
Найдите наибольший общий делитель пары чисел a и b путем разложения их на простые множители:
а) а = 36, b = 20; б) а = 1365, b = 1225; в) а = 1189, b = 589.
5.2. Первый шаг
Докажите, что если число а при делении на b дает остаток r, то
(a, b) = (b, r),
т. е. наибольший общий делитель пары чисел а и b совпадает с наибольшим общим делителем пары чисел b и r. Каким будет наибольший общий делитель пары чисел а и b, если число а делится на b нацело?
5.3. Алгоритм Евклида
Для нахождения наибольшего общего делителя пары натуральных чисел а1 и а2 поступают следующим образом: деля а1 на а2, получают остаток а3, затем, деля а2 на а3, получают остаток а4, затем, деля а3 на а4, получают остаток а5 и так далее до тех пор, пока некоторое число аn не разделится на аn+1 нацело. Запись этого алгоритма можно оформить так:
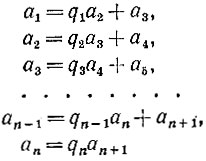
(числа q1, q2, ..., qn будем называть в дальнейшем последовательными частными).
Докажите, что описанный алгоритм обязательно закончится (т. е. при некотором значении n число аn разделится на аn+1 нацело), а число аn+1 окажется равным наибольшему общему делителю пары чисел а1 и а2.
5.4. Не разлагая на множители
Применяя алгоритм Евклида, найти наибольший общий делитель пары чисел а и b, указанных в п. а), б), в) задачи 5.1.
5.5. Найдя наибольший общий делитель
Сократите дробь: 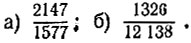
5.6. Разрезание на квадраты
На рис. 3 изображен прямоугольник размером 135*40, который разрезан на квадраты различной величины. Установите размеры квадратов и укажите связь между разрезанием на квадраты любого прямоугольника с целочисленными сторонами и алгоритмом Евклида (см. задачу 5.3).
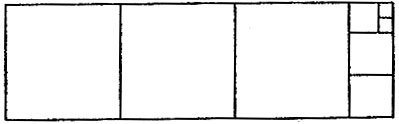
Рис. 3
5.7. Цепная дробь
Одним из применений алгоритма Евклида является представление дроби a1/a2 в виде
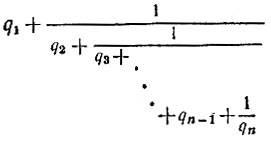
где q1 - целое число, a q2, q3, ..., qn - натуральные числа. Такое выражение называется цепной (конечной непрерывной) дробью. Докажите, что любую дробь a1/a2 можно разложить в цепную дробь, в которой числа q1, ..., qn являются последовательными частными алгоритма Евклида для нахождения наибольшего общего делителя пары чисел a1 и a2.
5.8. Разложение в цепную дробь
Разложите следующую дробь в цепную дробь:
а) 7/3; б) 84/39; в) 33/78.
5.9. Свертывание цепной дроби
Если в цепной дроби (см. задачу 5.7), начиная с конца, последовательно произвести указанные в ней операции по правилам действий с дробями, то в итоге получится обыкновенная дробь, разумеется, равная исходной.
Докажите, что полученная таким образом дробь будет несократимой. На основании этого утверждения сократите дробь 155/93, разложив ее в цепную дробь, а затем свернув в обыкновенную.
5.10. Подходящие дроби
Пусть задана цепная дробь с последовательными частными q1, q2, ..., qn (см. задачу 5.7). Выражения
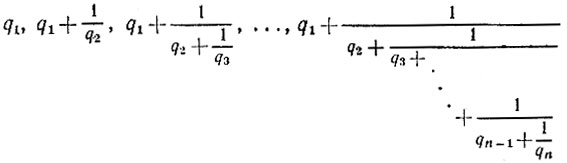
называются подходящими дробями порядка 1, 2, 3, ..., n соответственно. Разложите дробь 13/29 в цепную дробь и выпишите все подходящие к ней дроби. Обратите каждую из подходящих дробей в обыкновенную.
5.11. Комбинирование сопротивлений

Рис. 4
Из курса физики вам, наверняка, известно, что если соединить несколько сопротивлений R1, R2, ..., Rk в электрической цепи последовательно (рис. 4), то общее сопротивление будет равно R1 + R2 + ..., + Rk, а если соединить эти же сопротивления параллельно (рис. 5), то общее сопротивление окажется равным
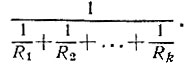
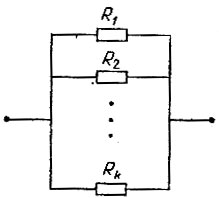
Рис. 5
А теперь представьте, что у вас есть большое количество одинаковых единичных сопротивлений. Можно ли, комбинируя их в электрической цепи специальным образом, составить схему, имеющую сопротивление:
а) 7/2; б) 10/7; в) вообще a/b?
5.12. Кое-что о подходящих дробях
Пусть для заданной цепной дроби с последовательными частными q1, q2, ..., qn несократимые дроби
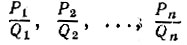
являются результатами свертывания подходящих дробей порядка 1, 2, ..., n соответственно (см. задачу 5.10). Докажите справедливость соотношений:
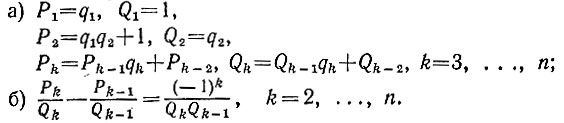
5.13. Приближение цепной дроби
Между двумя параллельными осями вращения требуется так установить зубчатую передачу, чтобы отношение угловых скоростей вращения было по возможности более близким к числу 355/113. Один из способов состоит в том, чтобы получить точное значение указанного отношения, поместив на одной оси шестеренку с 355 зубьями, а на другой - со 113 зубьями. Нельзя ли подобрать две шестеренки имеющие меньше 25 зубьев каждая, обеспечив при этом абсолютную погрешность, не превышающую 0,002?
Решения

5.1. а) Так как 36 = 22*32 и 20 = 22*5, то (36, 20) = 22 = 4.
б) Так как 1365 = 3*5*7*13 и 1225 = 52*72, то (1365, 1225) = 5*7 = 35.
в) Так как 1189 = 29*41 и 589 = 19*31, то (1189, 589) = 1.
5.2. Докажем, что все общие делители пары чисел а и b являются общими делителями пары чисел b и r и, наоборот, все общие делители пары чисел b и r являются общими делителями пары чисел а и b. Тогда и наибольшие общие делители обеих пар будут совпадать.
Пусть d - какой-нибудь общий делитель чисел а и b. Так как a = qb + r, то число r = a - qb также делится на d (ибо оно есть разность чисел а и qb, кратных d). Поэтому число d является общим делителем чисел b и г. Аналогично, если числа b и r имеют общий делитель d, то тот же делитель будет иметь и число a = qb + r, т. е. число d будет общим делителем чисел а и b.
В случае r = 0 получаем, что наибольший общий делитель пары чисел а и b равен наибольшему делителю числа b (не равного нулю), т. е. самому числу b.
5.3. Заметим, что остаток от деления любого числа на число а обязательно меньше самого числа а. Поэтому последовательность ненулевых остатков удовлетворяет неравенствам
a2>a3>a4>a5>...>0
и не может быть бесконечной, так как она содержит не более a2 чисел. Следовательно, описанный алгоритм не может продолжаться бесконечно. Если же число an разделится на аn+1 нацело, то, согласно результату задачи 5.2, будут выполнены равенства
(a1, a2) = (a2, a3) = (a3, a4) = ... = (an
, an+1) = an+1,
т. е. наибольший общий делитель пары чисел a1 и a2 будет равен an+1.
5.4. а) Так как
36 = 1*20 + 16, 20 = 1*16 + 4, 16 = 4*4,
то (36, 20) = 4.
б) Так как
1365 = 1*1225 + 140, 1225 = 8*140 + 105, 140 = 1*105 + 35, 105 = 3*35,
то (1365, 1225) = 35.
в) Так как
1189 = 2*589 + 11, 589 = 53*11 + 6, 11 = 1*6 + 5, 6 = 1*5 + 1, 5 = 1*5,
то (1189, 589) = 1.
5.5. Найдем наибольший общий делитель пары чисел, стоящих в числителе и знаменателе дроби, и сократим дробь на этот делитель.
а) Воспользуемся алгоритмом Евклида:
2147 = 1*1577 + 570, 437 = 3*133 + 38,
1577 = 2*570 + 437, 133 = 3*38+19,
570 = 1*437 + 133, 38 = 2*19,
откуда (2147, 1577) = 19. Произведя деление числителя и знаменателя дроби на 19, находим
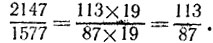
б) Заметим вначале, что числитель и знаменатель исходной дроби делятся на 6, поэтому ее можно сократить на 6 и получить дробь 221/2023. Теперь применим алгоритм Евклида:
2023 = 9*221 + 34, 221 = 6*34 + 17, 34 = 2*17.
Таким образом, (2023, 221) = 17 и дробь можно сократить еще на 17:
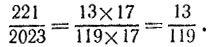
5.6. Из прямоугольника размером 135*40 сначала вырезаны квадраты со стороной, равной меньшей стороне этого прямоугольника, т.е. 40. Количество таких квадратов равно частному от деления 135 на 40 с остатком:
135 = 3*40 + 15.
Из оставшегося прямоугольника размером 40*15 вырезаны квадраты со стороной 15, которых, согласно делению 40 на 15 с остатком
40= 2*15 + 10,
можно вырезать два. Из оставшегося прямоугольника размером 15*10 вырезан один квадрат со стороной 10, что соответствует делению 15 на 10 с остатком:
15 = 1*10 + 5.
Наконец, последний прямоугольник размером 10*5 разрезан на два квадрата со стороной 5, так как
10 = 2*5.
Как показывает приведенный анализ, рассмотренный способ разрезания на квадраты прямоугольника размером а1*а2, по существу, является демонстрацией алгоритма Евклида нахождения наибольшего общего делителя пары чисел а1 = 135 и а2 = 40. Вообще прямоугольник размером а1*а2 можно разрезать на квадраты со сторонами а2, а3, а4, ..., аn+1 в полном согласии с формулами алгоритма Евклида (см. задачу 5.3), причем последовательные частные q1, q2, ..., qn укажут количества соответствующих квадратов.
5.7. Цепочку равенств, получающихся при нахождении наибольшего общего делителя пары чисел а1 и а2 с помощью алгоритма Евклида (см. задачу 5.3), перепишем следующим образом:

Подставляя в первую строчку вместо дроби а2/а3 ее выражение из второй строчки, находим
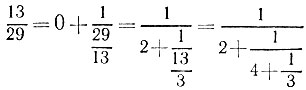
Подставляя сюда вместо дроби а3/а4 ее выражение из третьей строчки, имеем
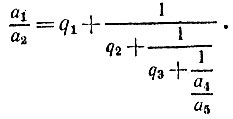
Производя аналогичные подстановки и далее, из предпоследней строчки получим равенство
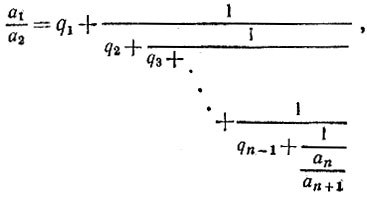
в котором останется лишь подставить вместо дроби 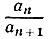 ее значение qn из последней строчки, после чего выражение будет удовлетворять всем требованиям задачи: все числа q2, q3, ..., qn являются натуральными, так как а2>а3>...>an-1>an>an+1, а число q1 является целым (если a1≥a2, то натуральным, а если а1<а2, то нулевым).
ее значение qn из последней строчки, после чего выражение будет удовлетворять всем требованиям задачи: все числа q2, q3, ..., qn являются натуральными, так как а2>а3>...>an-1>an>an+1, а число q1 является целым (если a1≥a2, то натуральным, а если а1<а2, то нулевым).
5.8.
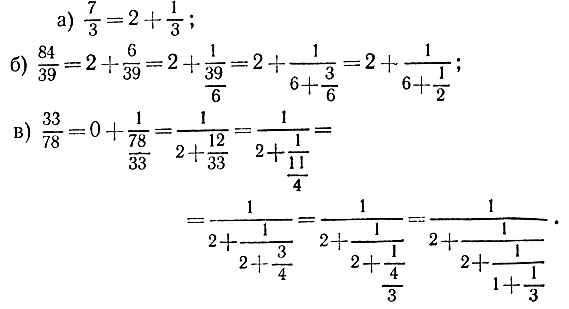
5.9. Последовательные операции по свертыванию цепной дроби сводятся к операциям двух типов: сложение 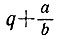 и деление
и деление 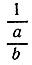 . Докажем, что если a/b несократимая дробь, то в результате операции любого из указанных двух типов получается также несократимая дробь. Действительно, операция первого типа приводит к дроби
. Докажем, что если a/b несократимая дробь, то в результате операции любого из указанных двух типов получается также несократимая дробь. Действительно, операция первого типа приводит к дроби 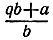 , числитель и знаменатель которой не имеют общих делителей, поскольку (см. решение задачи 5.2) справедливы равенства (qb + a, b) = (b, a) = 1. Операция второго типа приводит к дроби b/a которая также несократима, ибо (a, b) = (b, а) = 1. Таким образом, раз дробь 1/qn несократима, то на каждом шагу, в том числе и на последнем, при свертывании цепной дроби мы получаем несократимую дробь.
, числитель и знаменатель которой не имеют общих делителей, поскольку (см. решение задачи 5.2) справедливы равенства (qb + a, b) = (b, a) = 1. Операция второго типа приводит к дроби b/a которая также несократима, ибо (a, b) = (b, а) = 1. Таким образом, раз дробь 1/qn несократима, то на каждом шагу, в том числе и на последнем, при свертывании цепной дроби мы получаем несократимую дробь.
Например, для заданной в задаче сократимой дроби имеем
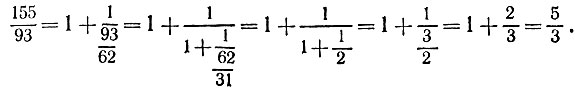
5.10. Для дроби
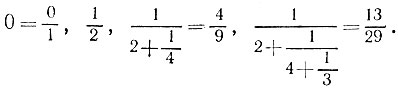
имеем следующие подходящие дроби:
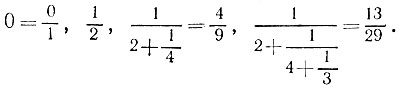
5.11. Решение этой задачи может показаться на первый взгляд совсем очевидным, поскольку для любой дроби a/b можно сначала соединить параллельно b единичных сопротивлений, получив сопротивление, равное 1/b, а затем размножить эту схему в а экземплярах, соединив их последовательно. При этом в конечном счете нам понадобится а*b единичных сопротивлений. Например, для такого решения п. а) их нужно 7*2 = 14 штук, а для решения п. б) -10*7 = 70 штук. Как показывает приводимое ниже решение, этот очевидный способ далеко не самый экономный: в п. а) достаточно иметь всего 5, а в п. б) - 6 сопротивлений.
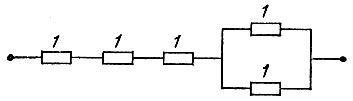
Рис. 6
а) Соединив параллельно два единичных сопротивления, получим сопротивление 1/2. Присоединив к нему последовательно еще три единичных сопротивления, мы получим сопротивление 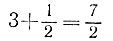 (рис. 6).
(рис. 6).
б) С учетом разложения 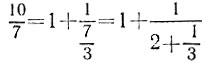 требуемое сопротивление можно получить следующим образом: соединим последовательно одно единичное сопротивление и блок, в котором параллельно соединены три сопротивления - два единичных и блок из трех последовательных единичных сопротивлений (рис. 7). Тогда сопротивление второго блока будет равно 3, а первого - будет равно
требуемое сопротивление можно получить следующим образом: соединим последовательно одно единичное сопротивление и блок, в котором параллельно соединены три сопротивления - два единичных и блок из трех последовательных единичных сопротивлений (рис. 7). Тогда сопротивление второго блока будет равно 3, а первого - будет равно 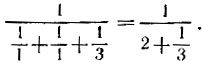 Общее же сопротивление как раз и будет составлять 10/7.
Общее же сопротивление как раз и будет составлять 10/7.
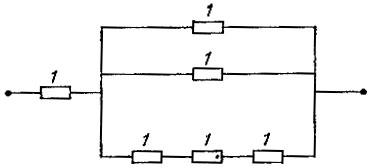
Рис. 7
в) Пусть дробь a/b разложена в цепную дробь (см. задачу 5.7)
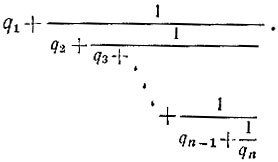
Тогда соединим последовательно q1 единичных сопротивлений и первый блок, в котором соединим параллельно q2 единичных сопротивлений и второй блок, в котором соединим последовательно q3 единичных сопротивлений и третий блок и т. д. Так, чередуя последовательное и параллельное соединения при составлении каждого последующего блока, мы на предпоследнем шаге соединим последовательно или параллельно qn-1 единичных сопротивлений и (n-1)-й блок, в котором соединим, наоборот, параллельно или последовательно qn единичных сопротивлений. Всего нам понадобится q1 + q2 + ... + qn сопротивлений, что, как правило, меньше, чем a*b.
Докажем, что полученная схема имеет сопротивление a/b. Если мы временно отсоединим от цепи весь первый блок, то сопротивление будет равно q1, т. е. первой подходящей дроби к данной цепной дроби. Если временно отсоединим от цепи не первый, а второй блок, то сопротивление неполного первого блока будет равно 1/q2 и общее сопротивление будет равно 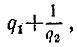 т. е. второй подходящей дроби. Если отсоединим от цепи не второй, а третий блок, то сопротивление неполного второго блока будет равно q3, первого -
т. е. второй подходящей дроби. Если отсоединим от цепи не второй, а третий блок, то сопротивление неполного второго блока будет равно q3, первого -
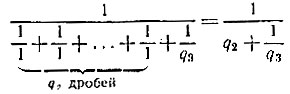
и общее сопротивление будет равно третьей подходящей дроби. Продолжая эти рассуждения до конца, мы придем к тому, что если отсоединить только (n-1)-й блок, то общее сопротивление будет равно (n-1)-й подходящей дроби. Наконец, если ничего не отсоединять, то общее сопротивление будет равно последней подходящей дроби, т. е. самой цепной дроби, равной a/b.
5.12. а) Так как 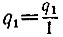 - несократимая дробь, то P1 = q1, Q1 = 1. Так как
- несократимая дробь, то P1 = q1, Q1 = 1. Так как 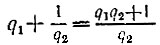 - несократимая дробь, то P2 = q1q2 + 1, Q2 = q2. Для k = 3 получаем
- несократимая дробь, то P2 = q1q2 + 1, Q2 = q2. Для k = 3 получаем
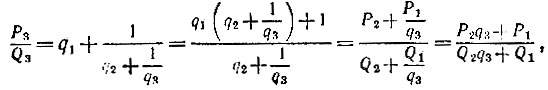
откуда имеем Р3 = Р2q3 + Р1, Q3 = Q2q3 + Q1, т. е. при k = 3 формулы справедливы, Пусть они уже доказаны для значения k-1:
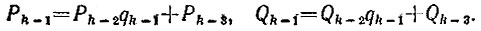
Тогда, заменяя qk-1 выражением 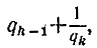 мы из дроби
мы из дроби 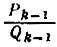 получим k-ю подходящую дробь
получим k-ю подходящую дробь
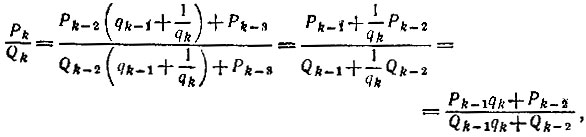
откуда имеем Pk = Рk-1qk + Рk-2, Qk = Qk-1qk + Qk-2, т.е. формулы справедливы и для значения k (несократимость каждой из дробей 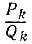 была доказана в решении задачи 5.9).
была доказана в решении задачи 5.9).
б) В силу формул п. а) при k = 2, ..., n имеем
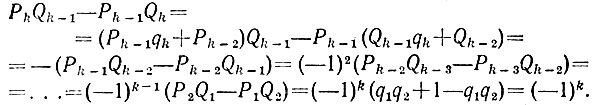
Поэтому для любого значения k = 2, ..., n получаем
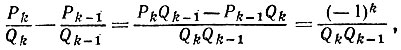
что и требовалось доказать,
5.13. Если бы мы захотели приблизить данную дробь 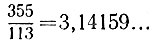 десятичной дробью
десятичной дробью 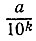 то для достижения заданной точности потребовалось бы подобрать значения a и k из неравенства
то для достижения заданной точности потребовалось бы подобрать значения a и k из неравенства 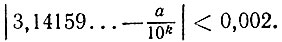 Проверка дробей
Проверка дробей 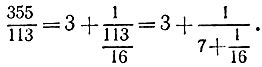 показывает их непригодность и убеждает нас в том, что такой перебор значений весьма затруднителен, да и вряд ли приведет к успеху".
показывает их непригодность и убеждает нас в том, что такой перебор значений весьма затруднителен, да и вряд ли приведет к успеху".
Попробуем приблизить данную дробь с помощью подходящих дробей к цепной дроби
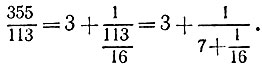
Первая подходящая дробь 3/1 дает погрешность 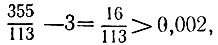 а значит, не годится. Зато вторая подходящая дробь, равная 22/7, отличается от третьей, равной исходной дроби, на величину
а значит, не годится. Зато вторая подходящая дробь, равная 22/7, отличается от третьей, равной исходной дроби, на величину
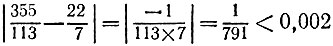
(см. соотношение п. б) задачи 5.12 при k = 3). Таким образом, шестеренки с 22 и 7 зубьями удовлетворяют всем условиям задачи.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'