
§ 4. Простое или составное?

При решении многих практических задач, в которых участвуют натуральные числа, немаловажную роль играет разложение этих чисел на множители, Основными "кирпичиками" в таком разложении являются простые числа, т. е. числа, большие 1 и делящиеся только на 1 и на себя. Остальные натуральные числа, большие 1, называются составными (число 1 не относится ни к простым, ни к составным). Основная теорема арифметики гласит, что всякое натуральное число, кроме 1, может быть представлено в виде произведения простых множителей, причем это представление единственно, если отвлечься от порядка множителей.
Издавна математиков интересовали вопросы о количестве и других свойствах простых чисел, а также о возможностях разложения конкретных чисел на простые множители. Еще Евклидом было доказано, что простых чисел бесконечно много. Древнегреческому математику Эратосфену был известен удобный способ отыскания простых чисел, который был назван решетом Эратосфена. Благодаря титаническим усилиям ряда ученых удалось получить ответы на многие, но пока не на все вопросы, связанные с распределением простых чисел в натуральном ряду. Что же касается разложения чисел на простые множители, то эта задача для больших чисел остается довольно трудной и по сей день.
4.1. Составные числа
Докажите, что составных чисел бесконечно много,
4.2. Теорема Евклида
Докажите, что простых чисел бесконечно много.
4.3. Простые числа - соседи
Могут ли два простых числа оказаться идущими подряд? А три?
4.4. Составные числа - соседи
Найдите пять последовательных натуральных чисел, каждое из которых является составным. Для любого ли натурального значения n можно подобрать n таких чисел?
4.5. Простое или составное?
Чтобы узнать, является ли данное натуральное число n составным, достаточно проверить, имеет ли оно хотя бы один делитель, больший 1 и меньший n. Докажите, что эту работу можно сократить, ограничившись проверкой делимости числа n только на простые числа и к тому же не превосходящие 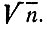
4.6. Простое или составное?
Разложить на простые множители число: а) 315; б) 127; в) 1001; г) 899; д) 919.
4.7. Решето Эратосфена
Выпишем подряд все натуральные числа от 1 до некоторого числа п и зачеркнем число 1. Возьмем первое незачеркнутое число, большее 1,- это будет число 2,- и зачеркнем каждое второе число, начиная отсчет от числа 2+1. Затем возьмем первое незачеркнутое число, большее 2,- это будет число 3,- и зачеркнем каждое третье число, начиная отсчет от числа 3 + 1 (ранее зачеркнутые числа также отсчитываются). Затем возьмем первое незачеркнутое число, большее 3,- это будет число 5,- и зачеркнем каждое пятое число, начиная отсчет от числа 5 + 1. Продолжая действовать так и далее, остановимся тогда, когда первое незачеркнутое число, большее предыдущего, окажется большим 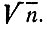 Докажите, что в итоге незачеркнутыми останутся все простые числа, не превосходящие n, и только они.
Докажите, что в итоге незачеркнутыми останутся все простые числа, не превосходящие n, и только они.
4.8. Первые 25 простых чисел
Используя решето Эратосфена, выпишите все простые числа, не превосходящие 100.
4.9. Еще несколько простых чисел
Выпишите все простые числа, находящиеся между числами 120 и 150.
4.10. Эйлерова модификация решета
Описанную в задаче 4.7 процедуру отыскания простых чисел можно упростить, если с самого начала не выписывать чисел, кратных 2, 3 или 5: Найдите все остатки от деления на 30, которые могут давать числа, не делящиеся ни на 2, ни на 3, ни на 5.
4.11. Попробуйте сами
Выпишите все простые числа, находящиеся между числами 470 и 520.
Решения

4.1. Все четные числа, большие 2 (а их бесконечно много), являются составными, так как каждое из них делится на 1, на себя и на 2.
4.2. Предположим, что утверждение задачи не верно, т. е. простые числа образуют лишь конечное множество, состоящее из чисел p1, p2, ..., pn. Рассмотрим число
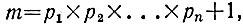
которое в силу основной теоремы арифметики делится хотя бы на одно из чисел p1, p2, ..., pn. Но тогда разность m - p1*p2*...*pn также делится на это число. С другой стороны, указанная разность равна 1 и не может делиться ни на одно из чисел p1, p2, ..., pn (больших 1). Полученное противоречие доказывает, что исходное предположение не верно, а утверждение задачи верно.
4.3. Если два простых числа идут подряд, то одно из них четно, а значит, равно 2 (см. решение задачи 4.1). Тогда второе число непременно равно 3, поскольку 1 не является простым числом. Итак, нами найдена единственная пара идущих подряд простых чисел. Отсюда следует, что тройки идущих подряд простых чисел не существует, так как из такой тройки можно было бы образовать две различные пары идущих подряд простых чисел, а именно первое число со вторым и второе с третьим.
4.4. Последовательные числа 24, 25, 26, 27, 28 образуют искомую пятерку. Докажем, что для любого натурального значения n найдутся n идущих подряд составных чисел. В самом деле, каждое из n чисел
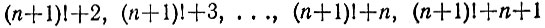
является составным, поскольку число
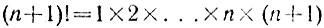
делится на 2, 3, ..., n и n+1, откуда первое число (n+1)!+2 делится на 2, второе число (n+1)!+3 делится на 3,..., (n-1)-е число (n+1)!+n делится на n, а n-е число (n+1)!+(n+1) делится на n+1.
4.5. Докажем, что любое составное число n имеет простой делитель, не превосходящий 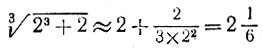 Возьмем наименьшее простое число р, участвующее в разложении числа n на простые множители. Тогда число n представляется в виде произведения pq, причем p≤q, поэтому p2≤pq = n и
Возьмем наименьшее простое число р, участвующее в разложении числа n на простые множители. Тогда число n представляется в виде произведения pq, причем p≤q, поэтому p2≤pq = n и 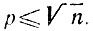 Из доказанного утверждения следует, что если число n не делится ни на одно простое число, не превосходящее
Из доказанного утверждения следует, что если число n не делится ни на одно простое число, не превосходящее 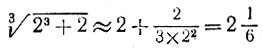 , то оно является простым.
, то оно является простым.
4.6.
а) 315 = 32*5*7;
б) 127 - простое число, так как оно не делится ни на одно из простых чисел 2, 3, 5, 7, 11, не превосходящих 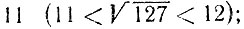
в) 1001 = 7*11*13;
г) 899 = 302-12 = 29*31;
д) 919 - простое число, так как оно не делится ни на одно из простых чисел, не превосходящих 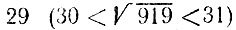
4.7. В результате описанной в условии задачи процедуры в ряду чисел от 1 до л не будет зачеркнуто ни одно простое число, так как на каждом шагу зачеркиваются только числа, кратные каким-то другим числам. Число k (большее 1) из этого ряда останется незачеркнутым только в том случае, если оно не делится ни на одно из незачеркнутых чисел, не превосходящих 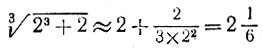 , среди которых содержатся все простые числа, не превосходящие
, среди которых содержатся все простые числа, не превосходящие 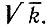 Согласно задаче 4.5, таким числом к может быть только простое число. Таким образом, в ряду останутся незачеркнутыми все простые числа и только они.
Согласно задаче 4.5, таким числом к может быть только простое число. Таким образом, в ряду останутся незачеркнутыми все простые числа и только они.
4.8. Зачеркнув в ряду чисел от 1 до 100 сначала число 1, затем числа, кратные 2, кроме числа 2, затем числа, кратные 3, кроме числа 3, затем числа, кратные 5, кроме числа 5, и, наконец, числа, кратные 7, кроме числа 7, мы получим следующий набор незачеркнутых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
На этом следует остановиться, поскольку следующее за числом 7 незачеркнутое число 11 уже превосходит 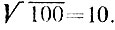
4.9. Так как 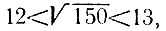 то наименьший простой делитель любого из составных чисел, меньших 150, не превосходит 11 (см. задачу 4.5). Вычеркнем из ряда чисел от 120 до 150 все числа, делящиеся на 2, 3 или 5, тогда останутся числа
то наименьший простой делитель любого из составных чисел, меньших 150, не превосходит 11 (см. задачу 4.5). Вычеркнем из ряда чисел от 120 до 150 все числа, делящиеся на 2, 3 или 5, тогда останутся числа
121, 127, 131, 133, 137, 139, 143, 149.
Учитывая, что число 121 делится на 11, а число 140 - на 7, находим среди оставшихся чисел все числа, кратные 11 или 7. Вычеркнув их, мы получаем ответ:
127, 131, 137, 139, 149.
4.10. Число не делится ни на 2, ни на 3, ни на 5 в том и только в том случае, если его остаток от деления на 30=2x3x5 не делится ни на одно из этих чисел. Так как
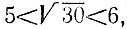
то, вычеркнув из всех возможных значений остатков от деления на 30, т. е. из чисел от 0 до 29, числа, кратные 2, 3 или 5, мы получим число 1 и все простые числа (см. задачу 4.7). Следовательно, набор искомых остатков выглядит так:
1, 7, 11, 13, 17, 19, 23, 29.
Благодаря этому наблюдению при отыскании простых чисел (больших 5) можно выписывать не все числа подряд, а только те, которые дают указанные здесь восемь остатков от деления на 30, что позволяет сэкономить работу по выписыванию в 30/8 = 3,75 раза. Именно так можно было поступить, например, при решении задачи 4.9.
4.11. Так как 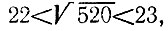 то наименьший простой делитель любого из составных чисел, меньших 520, не превосходит 19 (см. задачу 4.5). Согласно результату задачи 4.10, простые числа могут оказаться лишь среди 12 чисел
то наименьший простой делитель любого из составных чисел, меньших 520, не превосходит 19 (см. задачу 4.5). Согласно результату задачи 4.10, простые числа могут оказаться лишь среди 12 чисел
473, 479, 481, 487, 491, 493, 497, 499, 503, 509, 511, 517.
Из этих чисел теперь остается только вычеркнуть числа, кратные 7 (497, 511), кратные 11 (473, 517), кратные 13(503), кратные 17 (493) и кратные 19 (таких нет), и получить окончательный набор
479, 481, 487, 491, 499, 509.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'