
§ 6. По следам Диофанта

Самые разные задачи практического содержания часто приводят к уравнениям, в которых неизвестные по своему смыслу могут принимать только целочисленные значения. Уравнения в целых числах рассматривались еще в глубокой древности. Особенно много ими занимался александрийский математик Диофант, имя которого и носят уравнения в целых числах.
Простейшим примером диофантова уравнения служит линейное уравнение
ax + by = c
в целых числах (естественно, с целыми коэффициентами а, b и с). Оно может быть решено разными способами. Но, пожалуй, наиболее универсальный способ тесно связан, как это ни странно, с алгоритмом Евклида и цепными дробями (см. § 5).
6.1. Без сдачи
Докажите, что любую денежную сумму, выраженную целым числом рублей, большим 7, можно уплатить без сдачи, имея лишь трехрублевые и пятирублевые купюры в достаточном количестве.
6.2. Оплата покупки
Докажите, что за любую покупку стоимостью в целое число рублей можно заплатить одними трехрублевыми купюрами, если у кассира имеются только пятирублевые купюры. Какое наименьшее количество пятирублевых купюр достаточно при этом иметь кассиру?
6.3. Необходимое условие разрешимости
Пусть а, b, с - ненулевые целые числа. Докажите, что если число с не делится на наибольший общий делитель пары чисел а и b, то уравнение ах + bу = с в целых числах не имеет решений.
6.4. Сорока купюрами
Можно ли набрать сумму в 1000 рублей с помощью купюр достоинством в 1 рубль, 10 рублей, 100 рублей таким образом, чтобы всего было использовано ровно 40 купюр?
6.5. Затруднение кладовщика
На складе имеются гвозди, упакованные в ящики по 16 кг, 17 кг и 40 кг. Может ли кладовщик отпустить 140 кг гвоздей, не вскрывая ни одного ящика?
6.6. Линейные диофантовы уравнения
Покажите, как свести решение уравнения
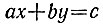
в целых числах с ненулевыми целыми коэффициентами а, b, с к решению уравнения
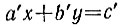
в целых числах, коэффициенты а', b', с' которого являются натуральными числами, причем числа а' и b' взаимно просты.
6.7. Состав с углем
На станцию привезли 420 т угля в вагонах вместимостью по 15 т, по 20 т и по 25 т. Сколько каких вагонов было использовано, если известно, что всего было 27 вагонов?
6.8. Общее решение
Пусть пара чисел x = x0, y = y0 удовлетворяет уравнению
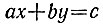
в целых числах с взаимно простыми коэффициентами а и b. Докажите, что формулы

с целым параметром k задают все решения этого уравнения,
6.9. Сколько нужно мешков?
Для перевозки зерна имеются мешки, в которые входит либо 60 кг, либо 80 кг зерна. Сколько надо заготовить тех и других мешков для загрузки 1 т зерна таким образом, чтобы все мешки были полными? Какое наименьшее количество мешков при этом может понадобиться?
6.10. Сколько нужно банок?
Требуется разлить 20,5 литра сока в банки по 0,7 л и 0,9 л так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?
6.11. Частное решение
Докажите, что уравнение
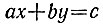
с взаимно простыми коэффициентами а и b имеет решение
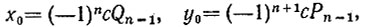
где 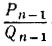 - предпоследняя подходящая дробь к цепной дроби, в которую раскладывается дробь a/b (см. задачи 5.7, 5.10, 5.12).
- предпоследняя подходящая дробь к цепной дроби, в которую раскладывается дробь a/b (см. задачи 5.7, 5.10, 5.12).
6.12. Загрузка трехтонок
Для перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трехтонные машины. Можно ли ими загружать машины полностью?
6.13. Целые точки на прямой
Сколько точек с целочисленными координатами, удовлетворяющими неравенствам х<0 и y>0, лежит на прямой
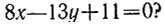
6.14. Наименьшим числом
У продавца имеются 100-граммовые гирьки и консервные банки весом по 450 г. Как с их помощью отвесить на чашечных весах 2,5 кг сахарного песка за один раз, используя для взвешивания наименьшее количество гирек и банок в общей сложности?
Решения

6.1. Пусть нужно уплатить денежную сумму в n рублей. Если число n делится на 3, то эту сумму можно уплатить одними трехрублевыми купюрами. Если остаток от деления числа n>7 на 3 равен 1, то
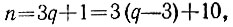
причем 3q + 1>7, откуда q>2 и, значит, в этом случае сумму можно уплатить q-3 трехрублевыми купюрами и двумя пятирублевыми. Если же остаток от деления числа n>7 на 3 равен 2, то
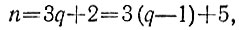
причем 3q + 2>7, откуда q>1 и, значит, в этом случае сумму можно уплатить q-1 трехрублевыми купюрами и 1 пятирублевой.
6.2. Если у кассира нет ни одной пятирублевой купюры, то покупатель может заплатить за покупку стоимостью в n рублей только при условии, что число n кратно 3. Если у кассира есть 1 пятирублевая купюра, то. покупатель может заплатить за покупку только при условии, что число n либо кратно 3, либо дает остаток 1 при делении на 3 (в последнем случае покупатель платит на 5 рублей больше и получает 5 рублей сдачи: n = 3q + 1 = 3(q + 2) - 5). Наконец, если кассир имеет 2 пятирублевые купюры, то покупатель может заплатить за покупку при любом значении n (в случае, когда остаток от деления числа n на 3 равен 2, покупатель может заплатить на 10 рублей больше и получить 10 рублей сдачи:
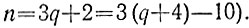
Таким образом, в условиях задачи кассир должен иметь минимум 2 пятирублевые купюры.
6.3. Пусть (a, b) = d и число с не делится на d. Тогда если уравнение 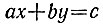 имеет целочисленное решение x = x0, y = y0, то справедливо числовое равенство ax0 + by0 = c, в котором левая часть делится на d (ибо числа а и b кратны d), а правая нет. Полученное противоречие доказывает, что указанное уравнение в целых числах не может иметь решений.
имеет целочисленное решение x = x0, y = y0, то справедливо числовое равенство ax0 + by0 = c, в котором левая часть делится на d (ибо числа а и b кратны d), а правая нет. Полученное противоречие доказывает, что указанное уравнение в целых числах не может иметь решений.
6.4. Если сумму в 1000 рублей можно набрать с помощью х, y и z купюр достоинством в 1 рубль, 10 рублей и 100 рублей соответственно, то справедливо равенство x + 10y + 100z = 1000. Если к тому же всего купюр должно быть x + y + z = 40, то целые числа x и y должны удовлетворять уравнению (40 - y - z) + 10y + 100z = 1000, или 9y + 99z = 960. Согласно утверждению задачи 6.3, последнее уравнение в целых числах не имеет решений, так как число 960 не делится на наибольший общий делитель пары чисел 9 и 99, равный 9.
6.5. Задача сводится к решению уравнения
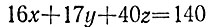
в целых неотрицательных числах. Заметим, что число y не может быть равным 0, так как иначе уравнение
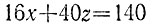
в целых числах имело бы решение, что противоречило бы утверждению задачи 6.3 (ибо число 140 не делится на число (16, 40)=8). Далее, число х также не может быть равным 0, так как иначе было бы выполнено равенство 17y = 140 - 40z = 10(14 - 4z) и неотрицательное число 14 - 4z делилось бы на 17 при целом неотрицательном значении z, что невозможно. Наконец, число z также не может быть равным 0, так как иначе из равенства 17y = 140 - 16x = 4(35 - 4x) следовало бы, что число 35 - 4x кратно 17 при x>0, что невозможно.
Таким образом, числа x, y, z должны быть положительными, а числа х' = х - 1, y' = y - 1, z' = z - 1 - целыми неотрицательными, удовлетворяющими уравнению
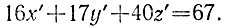
Аналогичные рассуждения показывают, что y'≠0 и х'≠0, т. е. числа х" = х' - 1 и y" = y' - 1 должны удовлетворять уравнению
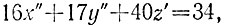
в целых неотрицательных числах, которое имеет единственное решение x" = 0, y" = 2, z' = 0. Таким образом, возвращаясь к исходным неизвестным, мы получаем единственное решение первоначального уравнения x = 2, y = 4, z = 1, т. е. 140 кг гвоздей можно отпустить только с помощью 2 ящиков по 16 кг, 4 ящиков по 17 кг и 1 ящика в 40 кг.
6.6. Если в правой части уравнения
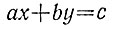
стоит отрицательное число, то умножим обе части уравнения на -1 и получим уравнение с положительным числом в правой части. Будем считать, что эта операция уже произведена с самого начала. Если коэффициент а отрицателен, то заменим неизвестную x неизвестной x' = -x и получим уравнение
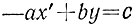
с положительным коэффициентом -а. Аналогично, если b<0, то замена y' = -y приводит к уравнению
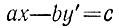
с положительным коэффициентом -b. Поэтому каждый из коэффициентов а и b соответствующей заменой неизвестной можно сделать положительным. Будем считать, что это уже сделано. Если числа а и b не являются взаимно простыми, то наибольший общий делитель (a, b) = d чисел а и b должен быть делителем числа с (иначе в силу утверждения задачи 6.3 уравнение в целых числах не будет иметь решений). Поэтому имеем a = a'd, b = b'd, c = c'd и, поделив обе части уравнения на d, получаем уравнение
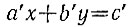
с взаимно простыми коэффициентами а' и b'.
6.7. Пусть было использовано x, y и z вагонов вместимостью по 15 т, по 20 т и по 25 т соответственно. Тогда имеем
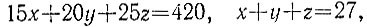
т. е. числа y и z должны удовлетворять уравнению
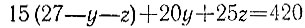
в натуральных числах. Преобразовывая это уравнение, получаем
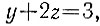
т. е. y = z = 1 и x = 25. Итак, было использовано 25 вагонов по 15 т, 1 вагон в 20 т и 1 вагон в 25 т.
6.8. Если пара чисел x, y наряду с парой чисел x0, y0 удовлетворяет уравнению
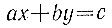
в целых числах с взаимно простыми коэффициентами а и b, то имеем ах + by = с = аx0 + by0, откуда а(x - x0) + b(y - y0) = 0. Так как число 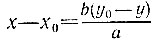 является целым, а числа b и а не имеют общих делителей, то число
является целым, а числа b и а не имеют общих делителей, то число 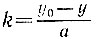 также является целым. Поэтому x - x0 = bk и y - y0 = ak, откуда получаем равенства
также является целым. Поэтому x - x0 = bk и y - y0 = ak, откуда получаем равенства

Мы доказали, что любое решение уравнения задается указанными формулами. С другой стороны, при любом целом значении к имеем
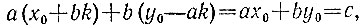
т. е. ничего кроме решений эти формулы не задают.
6.9. Для неизвестных x и y, обозначающих количество мешков по 60 и по 80 кг соответственно, имеем уравнение
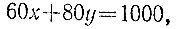
или уравнение
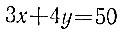
в целых неотрицательных числах. Одно целочисленное решение этого уравнения нетрудно угадать, воспользовавшись равенством
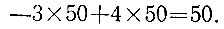
Учитывая формулы общего решения (см. задачу 6.8), получаем все целочисленные решения этого уравнения:
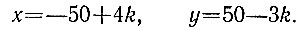
Теперь для того, чтобы найти все натуральные решения, наложим ограничения

из которых выведем оценки
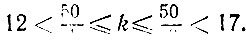
Таким образом, полагая последовательно k = 13, 14, 15, 16, найдем все неотрицательные решения:
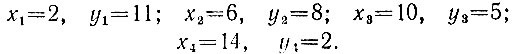
Наименьшее количество мешков x + y = 13 достигается при первом из найденных решений.
6.10. Задача сводится к решению уравнения
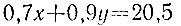
в целых неотрицательных числах (x и y - количество банок по 0,7 и 0,9 л соответственно). Преобразуем уравнение к виду
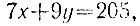
а затем, делая последовательные замены переменных в левой части, получим равенства
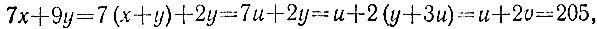
где x + y = u, y + 3u = v. Из этих равенств имеем
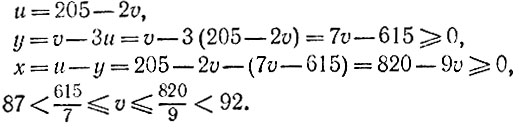
Подставляя u = 88, 89, 90, 91, получаем четыре решения:
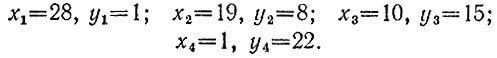
Наименьшая сумма x + y = 23 достигается при последнем решении, которое, следовательно, требует наименьшего
количества банок.
6.11. Из равенства, сформулированного в п. б) задачи 5.12, при k = n получаем
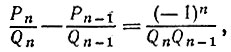
где 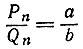 - последняя подходящая дробь к цепной дроби, в которую раскладывается дробь a/b. Так как дроби
- последняя подходящая дробь к цепной дроби, в которую раскладывается дробь a/b. Так как дроби 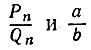 - несократимы (см. задачу 5.9), то Pn = а, Qn = b и
- несократимы (см. задачу 5.9), то Pn = а, Qn = b и
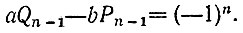
Умножая обе части последнего равенства на (-1)n, имеем
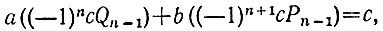
т. е. пара чисел 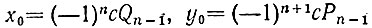 является решением уравнения ax + by = с.
является решением уравнения ax + by = с.
6.12. Обозначая через x и y количества контейнеров по 170 и 190 кг соответственно, получаем после сокращения на 10 уравнение
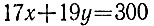
в целых неотрицательных числах. Для нахождения частного решения воспользуемся методом задачи 6.11, разложив дробь 17/19 в цепную дробь
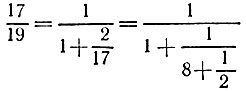
(число n получилось равным 4) и свернув предпоследнюю подходящую к ней дробь в обыкновенную
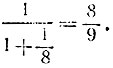
Итак, частное решение расходного уравнения имеет вид

а общее задается формулой
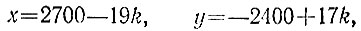
откуда получаем условия на параметр k
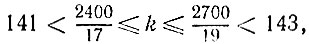
т. е. k = 142, x = 2, y = 14.
6.13. После замены переменной x' = -x (см. задачу 6.6) получаем уравнение
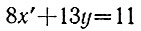
в натуральных числах, которое решим методами, предложенными в задачах 6.8 и 6.11: предпоследняя подходящая дробь к цепной дроби
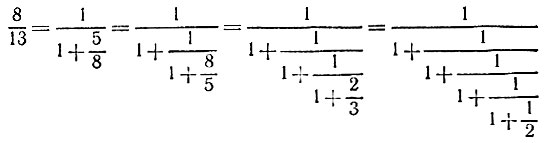
равна
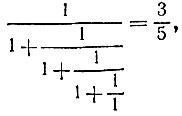
откуда
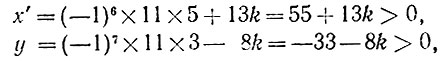
т. е. 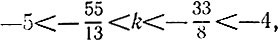 что невозможно. Итак, на прямой 8x - 13y + 11 = 0 нет ни одной точки с целочисленными координатами, удовлетворяющими условиям х<0 и y>0.
что невозможно. Итак, на прямой 8x - 13y + 11 = 0 нет ни одной точки с целочисленными координатами, удовлетворяющими условиям х<0 и y>0.
6.14. Так как гирьки и банки можно класть на любую чашку весов, то числа x и y (гирек и банок соответственно) удовлетворяют уравнению
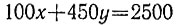
в целых числах (отрицательное значение какой-либо неизвестной означает, что соответствующие предметы лежат на одной чашке с сахарным песком). Приведем уравнение к виду
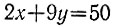
и заметим, что числа y0 = 0, x0 = 25 дают частное решение. Поэтому общее решение имеет вид (см. задачу 6.8)
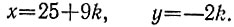
Докажем, что наименьшее количество гирек и банок, требуемое для взвешивания, равно 8. Действительно, если гирьки и банки лежат на одной чашке весов, то x≥0, y≥0 и -3<-25/9≤k≤0, причем наименьшая сумма x + y = 25 + 7k = 11 достигается при k = -2. Если гирьки лежат на одной чашке весов, а банки и сахар на другой, то x≥0, y≤0 и k≥0, причем наименьшая сумма x + (-y) = 25 + 11k = 25 достигается при k = 0. Если же банки лежат на одной чашке весов, а гирьки и сахар на другой, то x≤0, y≥0 и k≤-25/9<-2, причем наименьшая сумма (-x) + y = -25 - 11k = 8 достигается при k = -3. Таким образом, продавец должен на одну чашку весов положить 6 банок, а на другую - 2 гирьки и взвешиваемый сахар. Весы уравновесятся, если сахара будет 2,5 кг.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'