Кофейное воскресенье

Следующий день - не только воскресный, но и кофейный. Собираются, стало быть, у Мате, и Асмодей, который не раз заглядывал в его прежнее жилье (покойная тетка Мате, читавшая запоем, очень любила роман Лесажа и не раз брала его в библиотеке), еще раз с удовольствием убеждается, что сохранить в неприкосновенности свой замоскворецкий хаос хозяину все же не удалось. Что ни говорите, а новый дом - не старый дом! Никаких книг на полу. Электрические розетки в порядке. Зато самодельная кофеварка - гибрид электрочайника и алюминиевой кастрюльки - все та же. Кстати, она уже включена, и черт с наслаждением вдыхает густой кофейный аромат, которым насквозь пропитана вся небольшая квартира.

Кофейное воскресенье

По правде говоря, Мате побаивается, как бы кофе не испортил им нынешнего заседания. Вдруг он тоже подействует как снотворное?

Но бес опустошает чашку за чашкой, не проявляя никаких признаков сонливости. Напротив: узкие глазки его так и зыркают по сторонам, - дескать, что бы такое вытворить? Наконец, они останавливаются на телевизоре, и тут черт вдруг объявляет, что неплохо бы отдохнуть и посмотреть новую серию "Знатоков". "Знатоки" - его любимая передача (он ведь и сам знаток!), и отказаться от нее, хотя бы и во имя науки, он просто не в состоянии!

Филоматики встречают его предложение по-разному: Фило - с тайной радостью, Мате - с явным неудовольствием. Но Асмодей будто и не слышит его протестов! Он самолично включает приемник, потребовав наперед, чтобы все присутствующие, в том числе Пенелопа, Клеопатра и Буль, заняли свои места и потом уж не вздумали отлучаться. Он этого терпеть не может!

Наконец на экране появляются первые титры. Слышится знакомая музыка. И вдруг... Что такое? Кадры начинают мелькать как сумасшедшие, что-то трещит, гудит, и наконец изображение, а заодно и звук исчезают вовсе. Только и остается, что пустая освещенная поверхность.

Фило обиженно надувает губы. Вечная история! Только настроишься посмотреть хорошую передачу - и на тебе...

- Спокойствие, мсье! Только спокойствие! - призывает черт, не двигаясь с места. - Сейчас все будет в полном порядке. Недаром Хромой бес лучший телевизионный мастер на свете! Уж во всяком случае не хуже, чем Карлсон, который живет на крыше.

Он издали дует на телевизор, и тот снова оживает. Да, но куда же делись "Знатоки"? На экране титры совсем другой передачи!

- "Клуб знаменитых математиков", - читает Фило. - В первый раз слышу. Насколько я помню, в программе нет ничего подобного.

- В вашей программе, может, и нет, мсье. Зато в моей...

Мате понимающе вздергивает брови. Все ясно! Очередной адский фокус. Однако бранить беса он и не думает: передача-то как-никак математическая! Интересно, с чего она начнется? Наверное, как водится, со вступительной песенки... Так и есть! Звучит хорошо известная мелодия "Клуба знаменитых капитанов", к которой немного погодя присоединяется хор мужских голосов. Только поют они все же какие-то другие слова:

Клуб знаменитых математиков

Но вот хор умолкает, и на экране появляется какая-то комната. Вглядевшись в нее, филоматики взволнованно ахают: это же комната Паскаля на улице Сен-Мишель! Конечно: вот и знакомый диванчик. По-прежнему пылает огонь в очаге. Но теперь перед ним уже не два, а великое множество людей. И как только все они здесь уместились!

Поначалу друзья различают в толпе только Ферма и Паскаля. Лица остальных теряются в красочной сумятице одежд самых разных времен и национальностей (заметьте: черно-белое изображение телевизора Мате непонятным образом превратилось в цветное). Но потом Фило вдруг узнаёт Омара Хайяма^*, а Мате - Фибоначчи^**, и только вмешательство Асмодея не дает им влезть в экран с головой.

^* (Хайям Омар (около 1040-1131) - выдающийся поэт и ученый средневекового Востока, с которым филоматики познакомились во время предыдущих странствий.)

^** (Фибоначчи - прозвище средневекового итальянского математика Леонардо Пизанского (около 1170-1228), с которым Фило и Мате также успели уже познакомиться (см. книгу "Искатели необычайных автографов").)

Как раз в это время слово берет Ферма. Он объявляет очередное заседание Клуба знаменитых математиков открытым и предлагает избрать председателя на сегодняшний вечер.

- Так как тема нынешнего заседания - "Арифметический треугольник", - говорит Паскаль, - предлагаю избрать мэтра Пифагора.

Раздаются бурные рукоплескания, и с места поднимается смуглолицый грек в белом струящемся облачении.

- Благодарю высокое собрание за честь! - произносит он, с достоинством наклонив курчавобородую голову. - Хотя совершенно очевидно, что причина ее - не столько моя причастность к теме заседания, сколько уважение к древности. Потому что арифметическим треугольником я никогда не занимался.

- Зато ты занимался фигурными числами, которые в него входят, - возражает Хайям.

Пифагор протестующе поднимает руку.

- Не преувеличивай моих заслуг, о Хайям! Фигурные числа - не мое открытие. Много путешествуя, я, конечно, многое и запамятовал. Но фигурные числа я, помнится, вывез из Вавилона заодно с другими математическими редкостями.

- А все-таки узнали мы о них не от вавилонян, а от тебя и от твоего последователя Никомаха, - упорствует Хайям.

- Ну, если так, - Пифагор делает приглашающий жест, - тогда позволь предоставить слово тебе. Недаром ходят слухи, что Омар Хайям тоже имеет некоторое отношение к арифметическому треугольнику.

- Разве? - усмехается тот.- Другие всегда знают о нас больше, чем мы сами. Во всяком случае, если в моей жизни и было что-нибудь подобное, то сам я об этом начисто забыл. Зато наверняка помню, что арифметический треугольник был известен в Древней Индии и в Древнем Китае. А потому предоставь лучше слово мэтру Тарталье. Надеюсь, он-то свою причастность к арифметическому треугольнику отрицать не станет.

- Ни-ни-ни в коем случае, - подает голос высокий итальянец с глубокими шрамами на подбородке, одетый по моде шестнадцатого столетия. - Хотя числа в этом треугольнике я ра-ра-расположил так, что правильнее было бы называть его прямоугольником.

- Какое, однако, удивительное совпадение! - не выдерживает Фило. - "Тарталья" - по-итальянски "заика", а этот уважаемый мэтр и впрямь заикается.

- Ничего удивительного, - поясняет Асмодей. - Прозвище Тартальи сей даровитый синьор получил как раз за свое заикание, которое началось у него после сильного ранения в нижнюю челюсть.

- А настоящая его фамилия как? - продолжает приставать любопытный Фило.

Но Асмодей лишь досадливо пожимает плечами. Не всегда ж ему знать то, чего не знает никто! И вообще, дадут ему наконец смотреть передачу?

- Однако, до-до-дорогие мэтры, - продолжает Тарталья, - хочу обратить ваше внимание на то, что арифметические треугольники возникали в разные времена и в разных странах совершенно самостоятельно. Свой я, во-во-во всяком случае, придумал сам.

- И я тоже, достопочтенный мэтр Тарталья, - присоединяется Паскаль, - потому что ваши изыскания были мне, к сожалению, неизвестны.

- Вы забыли сказать главное, уважаемый мэтр Паскаль, - вмешивается представительный горбоносый красавец с густыми бархатными бровями и легкой любезной улыбкой в уголках рта.

- Насколько я понял, мэтр Лейбниц, вы просите слова, - строго намекает Пифагор. - Рад его вам предоставить.

Тот, извиняясь, склоняет набок голову в крутокудром каштановом парике. Достопочтенному председателю незачем затрудняться! Он, Лейбниц, хотел лишь заметить, что заслуга мэтра Паскаля не столько в том, что он открыл арифметический треугольник, сколько в том, что ему удалось вывести формулу сочетаний. Ту самую формулу, с помощью которой легко вычислить любой элемент числового треугольника.

- Прошу прощения! - живо перебивает Паскаль. - Одновременно со мной ту же формулу вывел мэтр Пьер Ферма.

- Не отрицаю! - весело басит Ферма. - И все-таки честь ознакомить собравшихся с некоторыми свойствами формулы сочетаний я предоставляю вам.

Паскаль молча кланяется и, подойдя к стоящей у камина грифельной доске, выписывает на ней две таблицы.

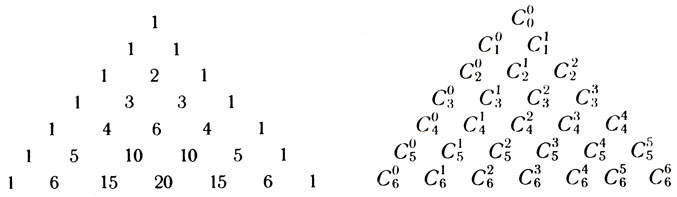
- Как видите, - поясняет он, - арифметический треугольник изображен здесь в двух видах: в числовом и условном, где каждый член его выражен через число сочетаний из номера строки по номеру своего места в ней. Разумеется, верхней строке и первому числу каждой строки присвоен нулевой номер. Далее обратите внимание на то, что все сочетания, у которых верхний индекс нуль, равны единице. Почему это так, понять нетрудно. Стоит только сравнить обе таблицы. Выберем, допустим, шестую строку (ее порядковый номер 5) и рассмотрим два ее числа, хотя бы 5 и 5. Одно из них в условном треугольнике обозначено как С₅¹, второе - как C₅⁴. Но ведь числа эти равны между собой, ибо каждое из них порознь равно 5: С₅¹ = С₅⁴ = 5. В свою очередь С₅¹ можно записать как С₅⁵⁴. И если это обобщить для любой строки (n) и любого порядкового числа в ней (m), то получится любопытное свойство сочетаний: С_n^m = С_n^n-m (це из эн по эм равно це из эн по эн минус эм). Отсюда ясно, что так как с одной стороны С_nⁿ = 1, а с другой

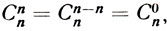
то и выходит, что

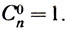
Ну, а дальше уж, для общности правила, условились и С₀⁰ тоже считать единицей. Вот вам простой и удобный способ отыскивать любое, даже самое большое число сочетаний. И потому вопрос, чему равно, скажем, число сочетаний из тысячи по девятисот девяноста девяти, не должен пугать даже школьника, - вычислить это проще простого:

- За-за-замечательно! - восхищается Тарталья. - Я бы до такого ни-ни-никогда не додумался.

- Не клевещите на себя, дорогой мэтр Тарталья, - протестует Паскаль. - Просто вы жили на сто лет раньше, и время формулы сочетаний еще не пришло. А теперь попрошу нашего досточтимого председателя предоставить слово мэтру Лейбницу, ибо я горю желанием узнать, что сделал с арифметическим треугольником он.

- С величайшим удовольствием! - кивает Пифагор. - Тем более, что я и сам давно дожидаюсь такого случая.

- Собственно говоря, я шел по стопам мэтра Паскаля, - уголками рта улыбается Лейбниц, - но мой треугольник составлен в обратном порядке. Так сказать, шиворот-навыворот. Прежде всего вместо целых чисел я взял дробные. А уж из этого вытекает и все остальное.

Он вытирает доску влажной тряпкой и пишет на ней другую таблицу.

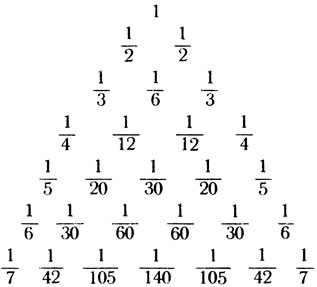
- Этот свой треугольник я назвал гармоническим, - поясняет он.

- Превосходно! - горячо одобряет Пифагор. - Всегда говорил, что главное в мире - гармония.

- Вполне с вами согласен, - кланяется Лейбниц. - Но название это объясняется тем, что в правом и левом наклонных рядах моего треугольника стоят числа, которые принято называть гармоническим рядом: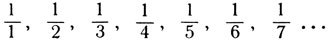  
Особенность этого ряда заключается в том, что сумма его членов: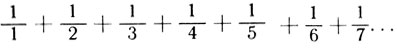  
не стремится ни к какому определенному числу - иначе говоря, она бесконечна. Не то что, скажем, другой ряд:  
сумма которого стремится к единице. Так вот, если в треугольнике мэтра Паскаля каждое число равно сумме двух чисел, стоящих над ним (справа и слева), то в моем треугольнике каждый член равен сумме чисел, стоящих под ним (также справа и слева). Например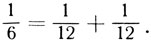  
А потому, если в треугольнике мэтра Паскаля общий член выражается формулой С_n^m, то в моем он выглядит так: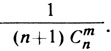  
Вот, например, в третьем ряду сверху второй член таков: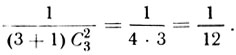  

- О-о-очень любопытно! - восклицает экспансивный Тарталья.

- Но это еще не всё! - продолжает Лейбниц. - Выберем какой-нибудь наклонный ряд - скажем, второй: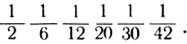  
Начнем вычисление с любого, хотя бы со второго его члена, то есть с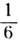  
Тогда из сказанного о законе образования членов треугольника прежде следуют такие равенства:

Сложим почленно правые и левые части этих равенств. Все равные слагаемые в левых частях, имеющие противоположные знаки (плюс и минус), взаимно уничтожатся, и останется только первое число ¹/₆. Значит,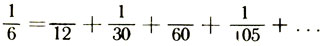  
Но ведь правая часть этого равенства есть сумма всех чисел следующего за этим наклонного ряда, начиная с ¹/₁₂ и до бесконечности. И если в треугольнике мэтра Паскаля каждый член равен конечной сумме чисел, стоящих слева и расположенных над данным числом, то в моем треугольнике каждое число равно бесконечной сумме чисел, стоящих справа и под данным.

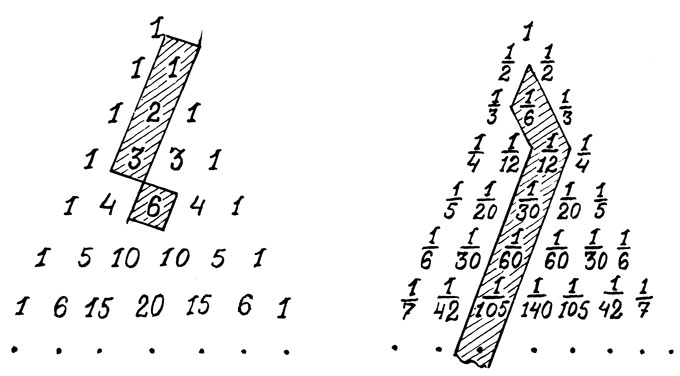
Вот, собственно, и всё.

Паскаль встает и горячо пожимает руку слегка утомленному оратору.

- Благодарю! Благодарю вас, многоуважаемый мэтр Лейбниц, от имени всех присутствующих, а от себя - особенно. Ваши бесконечные ряды доставили мне бесконечное удовольствие. Потому что бесконечность во всех ее проявлениях - предмет моего самого пристального внимания.

- Если так, - говорит Лейбниц, - попросите нашего достопочтенного председателя предоставить слово мэтру Ньютону, и вы получите удовольствие еще большее. Ибо он использовал вашу общую с мэтром Ферма формулу весьма неожиданно. Причем бесконечность в этом случает играет не последнюю роль.

Тут раздаются аплодисменты, и мэтр Исаак Ньютон, раскланиваясь, поднимается со своего места.

- Прежде чем перейти к сути дела, - говорит он, - хочу обратить ваше внимание на одно обстоятельство. Подобно мэтрам Паскалю и Ферма, мы с мэтром Лейбницем также совершили одно и то же открытие. Это дифференциальное и интегральное исчисление. Надо, однако, признать, что открытие это - всего лишь завершение того, что начато нашими предшественниками. В первую очередь мэтрами Паскалем и Ферма, а также отсутствующим здесь мэтром Декартом.

Слова его встречены бурным одобрением. Все встают и долго рукоплещут.

- А теперь перейдем к вопросу, затронутому мэтром Лейбницем, - продолжает Ньютон, дождавшись тишины. - Должен снова оговориться. Формула разложения степени бинома носит мое имя не совсем справедливо. Ею пользовались задолго до меня. О моей роли в ее судьбе я как раз собираюсь рассказать. Для начала запишу эту формулу в ее обычном виде.

Он вытирает доску, и на ней появляется следующее выражение:

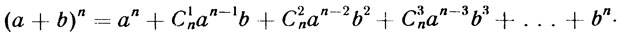
- Здесь, - поясняет он, - коэффициенты в каждом члене, как вам уже известно, есть сочетания из п по нулю, по единице, по два, по три и так далее, то есть

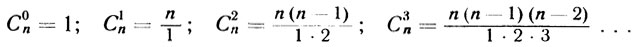
Что же нового внес в эту формулу я? Только то, что предложил обобщить ее, иначе говоря, не ограничивать целым числом для n, а распространить на любые значения показателя степени - дробные, отрицательные... При этом формула сочетаний, выведенная мэтрами Паскалем и Ферма, тоже становится обобщенной. Что же касается самой степени бинома, то она раскладывается в бесконечный ряд. - Тут мэтр Ньютон предупредительно оборачивается к Паскалю. - Вот в каком виде я предлагаю ее записывать:

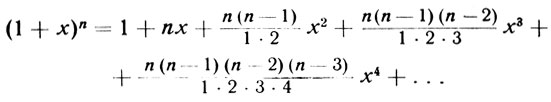
Например, для n = ¹/₂ получится такой ряд:

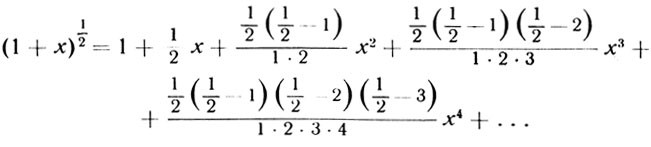
Или

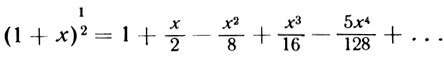
Сохраняя любое число слагаемых в правой части, можно вычислить эту сумму с любой степенью точности. Само собой разумеется, что икс в нашей формуле меньше единицы.

Отвесив учтивый поклон, мэтр Ньютон садится, и Пифагор собирается уже объявить следующего оратора... Но тут в телевизоре что-то щелкает, и место Пифагора занимают Знатоки, сообща арестующие разоблаченного преступника.

Мате с досадой хлопает себя по коленке. Опять на самом интересном месте... Черт знает что!

- Вот именно, мсье, - сейчас же откликается Асмодей. - Я, во всяком случае, всегда знаю, что делаю. Кроме того, привычка - вторая натура, как сказал Цицерон. А он тоже знал, что говорил.