Заключение

Газеты приносят вести о все новых катастрофах. Землетрясения, наводнения, взрывы, войны, эпидемии окружают нас со всех сторон,5 и вдобавок над всем земным шаром нависает угроза страшнейшей из катастроф - ядерной. Пора запретить атомную гражданскую войну.

Математическая теория катастроф сама по себе не предотвращает катастрофы, подобно тому, как таблица умножения,, при всей ее полезности для бухгалтерского учета не спасает ни от хищений отдельных лиц, ни от неразумной организации экономики в целом.

Математические модели катастроф указывают, однако, некоторые общие черты самых разных явлений скачкообразного изменения режима системы в ответ на плавное изменение внешних условий. Например, устойчивый установившийся режим (скажем, режим работы реактора, или экологический или экономический режим) обычно погибает либо столкнувшись с неустойчивым (причем в момент столкновения скорость конвергенции бесконечно велика), либо вследствие нарастания (опять бесконечно быстрого) самоподдерживающихся колебаний. Это объясняет, почему так трудно бороться с катастрофой, когда ее признаки сделались уже заметными: скорость ее приближения неограниченно возрастает по мере приближения к катастрофе.

К катастрофической потере устойчивости может приводить оптимизация и интенсификация. Например,: для простейшей модели рыболовства

оптимизация (максимизация) квоты отлова с = 1/4 приводит к неустойчивости установившегося режима (рис. 85) и катастрофе - уничтожению популяции малыми случайными колебаниями.

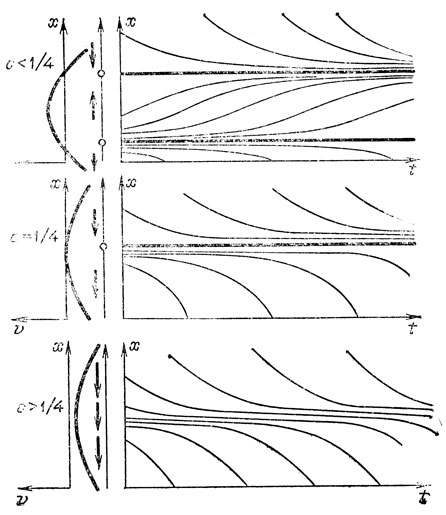
Рис. 85. Катастрофическая потеря устойчивости при оптимизации в простейшей модели рыболовства с учетом конкуренции за пищу

Устойчивость не теряется, если ввести обратную связь: жесткий план с заменить величиной, пропорциональной фактически имеющимся ресурсам (урожаю, популяции,..). В модели с обратной связью (рис. 86)

оптимальное значение коэффициента к равно 1/2. При таком выборе установится средний многолетний вылов kх₀ = 1/4. Это - такой же вылов, как максимальный жесткий план отлова (большая производительность в этой системе невозможна).

Но в то время как при максимальном жестком плане система теряет устойчивость и самоуничтожается, введение обратной связи стабилизирует ее и, например, небольшие изменения коэффициента k (или иные случайности) приведут лишь к небольшому уменьшению производительности, а вовсе не к катастрофе.

Управление без обратной связи всегда приводит к катастрофам: важно, чтобы лица и организации, принимающие ответственные решения, лично, материально зависели от последствий этих решений.

Агрессоры, развязывающие войны или межнациональную вражду, обычно считают, что они не будут нести личной ответственности за последствия, а боязнь личного ядерно-лагерного уничтожения служит важным сдерживающим фактором.

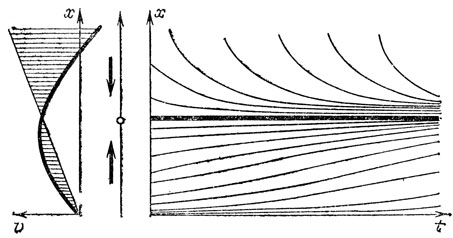
Рис. 86. Стабилизация при замене жесткого плана обратной связью

Ученые, исследовавшие модели гонки вооружений, еще в 60-х годах предсказали, что введение разделяющихся боеголовок повлечет потерю устойчивости стратегического равновесия. Они предсказали также, что если дипломатическим путем удастся благополучно миновать этот опасный период, то дальнейшее удорожание вооружения стабилизирует ситуацию и устойчивость может восстановиться.

Нынешняя перестройка во многом объясняется тем, что начали действовать хотя бы некоторые механизмы обратной связи (боязнь личного уничтожения).

Трудность проблемы перестройки связана с ее нелинейностью. Привычные методы управления, при которых результаты пропорциональны усилиям, тут не действуют, и нужно вырабатывать специфически нелинейную интуицию, основанную на порой парадоксальных выводах нелинейной теории.

Математическая теория перестроек была создана задолго до нынешней перестройки. Вот некоторые простейшие качественные выводы из этой теории применительно к нелинейной системе, находящейся в установившемся устойчивом состоянии, признанном, плохим, поскольку в пределах видимости имеется лучшее, предпочтительное устойчивое состояние системы (рис. 87).

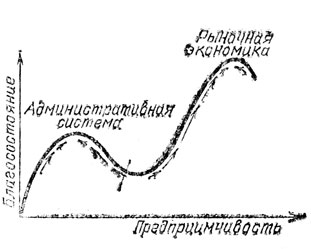
Рис. 87. Перестройка с точки зрения теории перестроек

1. Постепенное движение в сторону лучшего состояния сразу же приводит к ухудшению. Скорость ухудшения при равномерном движении к лучшему состоянию увеличивается.

2. По мере движения от худшего состояния к лучшему сопротивление системы изменению ее состояния растет.

3. Максимум сопротивления достигается раньше, чем самое плохое состояние, через которое нужно пройти для достижения лучшего состояния. После прохождения максимума сопротивления состояние продолжает ухудшаться.

4. По мере приближения к самому плохому состоянию на пути перестройки сопротивление, начиная с некоторого момента, начинает уменьшаться, и как только самое плохое состояние пройдено, не только полностью исчезает сопротивление, но система начинает притягиваться к лучшему состоянию.

5. Величина ухудшения, необходимого для перехода в лучшее состояние, сравнима с финальным улучшением и увеличивается по мере совершенствования системы. Слабо развитая система может перейти в лучшее состояние почти без предварительного ухудшения, в то время как развитая система, в силу своей устойчивости, на такое постепенное, непрерывное улучшение неспособна.

6. Если систему удается сразу, скачком, а не непрерывно, перевести из плохого устойчивого состояния достаточно близко к хорошему, то дальше она сама собой будет эволюционировать в сторону хорошего состояния.

С этими объективными законами функционирования нелинейных систем нельзя не считаться. Выше сформулированы лишь простейшие качественные выводы. Теория доставляет также количественные модели, но качественные выводы представляются более важными и в то же время более надежными: они мало зависят от деталей функционирования системы, устройство которой и численные параметры могут быть недостаточно известными.

Наполеон критиковал Лапласа за "попытку ввести в управление дух бесконечно малых". Математическая теория перестроек - это та часть современного анализа бесконечно малых, без которой сознательное управление сложными и плохо известными нелинейными системами практически невозможно.

Не требуется, однако, специальной математической теории, чтобы понять, что пренебрежение законами природы и общества (будь то закон тяготения, закон стоимости или необходимость обратной связи), падение компетентности специалистов и отсутствие личной ответственности за принимаемые решения приводит рано или поздно к катастрофе.