Ответы и указания

1.1. В соответствии с аксиомой (теоремой): через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну. Четыре же точки могут не лежать в одной плоскости.

1.2. Недостаточно, ибо он таким образом мог установить лишь, является ли лоскут ромбом.

1.6. |х-2| есть расстояние от точки X до точки 2. |х - 2|+|х-5| есть сумма расстояний от точки X до точек 2 и 5. Эта сумма всегда больше 5-2=3. Поэтому уравнение не имеет решений при а<3.

1.7. Каждому четному числу 2n соответствует одно и только одно нечетное число 2n-1, поэтому количество их одинаково в натуральном ряду.

1.8. Причина в том, что сравниваются бесконечные множества чисел, а не конечные.

2.1. а) Круг; б) окружность; в) прямоугольник.

2.2. Натуральные числа. Можно решить, например, такую задачу: "Зная номер человека в очереди и сколько времени в среднем занимает обслуживание одного покупателя, узнать, сколько времени ему придется стоять в очереди".

2.3. Математическое описание поездки велосипедиста можно сделать с помощью графика.

3.1. Существенные: а, в, несущественные: б, г и д.

3.2. Математические объекты одного и того же вида составляют объем соответствующего математического понятия.

3.3. Суждения: б, г.

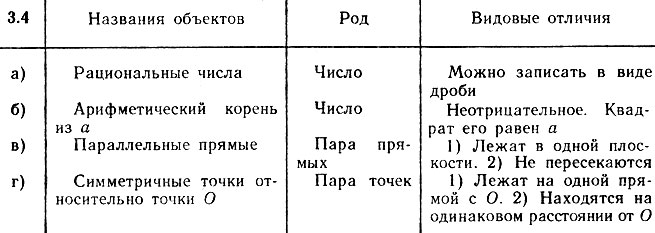
3.5. Замкнутая кривая, описанная концом отрезка, который вращается на плоскости вокруг своего другого неподвижного конца, называется окружностью.

3.6. Индуктивное определение: каждый член последовательности Фибоначчи, начиная с третьего, равен сумме двух предшествующих членов. Первые два члена последовательности задаются особо.

3.7. Две прямые называются перпендикулярными, если при их пересечении образуются прямые углы.

3.9. Если для всякого n верно, что а_n+1>а_n, то последовательность a₁, а₂, ..., а_n, ... называется возрастающей.

3.10. Да.

3.11. а) Прямоугольник или ромб; б) произведение; в) пара углов; г) натуральные числа; д) отрезок.

3.12. Фигура, многоугольник, четырехугольник, параллелограмм.

3.13. Не нужно и нельзя.

4.1.

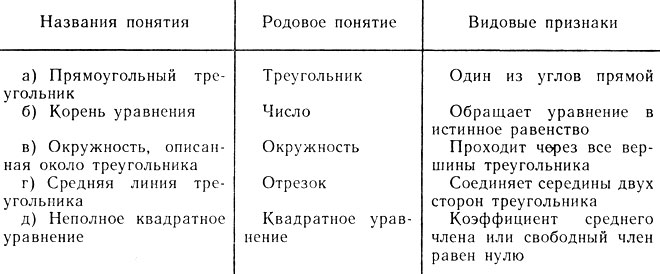
4.2. а) Обычно биссектрисой треугольника называют не прямую, а отрезок, делящий угол треугольника пополам от вершины до точки противоположной стороны, б) Пропущен признак: лежат в одной плоскости, в) Правильное, г) и д) Тавтология, е) Лишний признак: равные, ж) Достаточно указать, что две смежные стороны равны, з) Правильное.

4.3. Крестом называется фигура, состоящая из двух пересекающихся пополам отрезков.

4.4. Осреднением двух дробей называется дробь, числитель которой равен сумме числителей данных дробей, а знаменатель - сумме знаменателей.

5.1. а) Дано: 1) Длина окружности радиуса R₁ равна С₁; 2)длина окружности радиуса R₂ равна С₂. Доказать:C₁/R₁=C₂/R₂ б) Дано: а и b - члены двучлена. Доказать: (a+b)²=a²+2ab+b²;

в) Дано: ab=0. Доказать: а=0 или b=0.

г) Дано: а>0, b>0. Доказать: log_nab = log_na+log_nb;

д) Дано: АВ и CD - диагонали ромба. Доказать: АВ⊥CD.

5.2 а) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. Верная теорема.

б) Частное от деления одинаковых степеней двух чисел равно той же степени частного этих чисел. Верная теорема.

в) Если натуральное число делится на 10, то его запись оканчивается нулем. Верная теорема.

г) Если в треугольнике два угла острые, то третий угол тупой или прямой. Неверная теорема.

5.3 а) Для того чтобы диагонали четырехугольника делились в точке пересечения пополам, необходимо и достаточно, чтобы четырехугольник был параллелограммом.

б) Для того чтобы один из корней квадратного уравнения был равен нулю, необходимо и достаточно, чтобы свободный член уравнения был равен нулю.

в) Для того чтобы сумма двух чисел была равна нулю, необходимо и достаточно, чтобы они были противоположными числами.

г) Для того чтобы проекции двух наклонных, проведенных из одной точки в одной прямой, были равны, необходимо и достаточно, чтобы эти наклонные были равны.

5.4. а), б), г) - достаточно.

5.5. а) А необходимо для В, В достаточно для А; б) необходимо для В, В достаточно для A; в) A достаточно для В, В необходимо для А.

6.1.

6.2. Ошибка в чертеже: биссектриса ВМ и срединный перпендикуляр DM пересекаются вне треугольника.

6.3. Воспользуйтесь второй эвристикой.

6.4. Ошибка в ссылке на теорему Пифагора. Надо было сослаться на теорему, обратную теореме Пифагора.

6.5. Пусть ∠А⊥ ∠В (1).

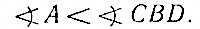Тр. доказать, что в ΔABC: ВС>АС. Допустим, что ВС=АС. Тогда по теореме об углах при основании равнобедренного треугольника ∠A=∠B, что противоречит условию (1). Допустим теперь, что BC<AC. Тогда отложим на АС отрезок CD=BC. По допущению точка D должна находиться между точками A и С, поэтому В то же время ∠CBD, как внешний для ΔABD, должен быть больше внутреннего, с ним не смежного. Значит, Сравнивая с (2), получаем, что 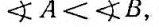, что противоречит (1). Следовательно, оба наши допущения неверны, тогда остается, что единственно верным соотношением между сторонами ВС и АС является то, что нам и требовалось доказать, а именно что ВС>АС.

6.6. Ошибка состоит в неправильном использовании второго признака равенства треугольников. В нем сказано, что треугольники равны, если сторона и два прилежащих к ней угла... Между тем в ΔАВМ угол АВМ не является прилежащим к стороне AM.

6.7. Ошибка в том, что для частного чисел не имеет место распределительный закон, и выносить общий множитель из делимого и делителя за скобки нельзя. Поэтому 4:4≠4 (1:1) и 5:5≠5 (1:1).

6.8. По условию (1) b-а<0, поэтому, умножая обе части (1) на b-а, надо было изменить знак неравенства на противоположный.

6.9. Это определение, его доказывать не нужно.

7.1. Потому что четность не является общим свойством рациональных чисел, оно присуще лишь целым числам.

7.2. а) Верно; б) неверно, ибо функции могут быть и невозрастающими и неубывающими, например у=x² при х<0 убывающая, а при x>0-возрастающая; в) верно; г) неверно, ибо квадрат есть частный случай ромба, а ромбы, не являющиеся квадратами, не являются и прямоугольниками.

7.3. Геометрические фигуры делятся на замкнутые (треугольник, окружность и т. д.) и незамкнутые (угол, прямая и т. д.).

7.4. Одна классификация рациональных чисел: отрицательные, нуль и положительные. Другая классификация: целые и дробные, целые в свою очередь делятся на натуральные, нуль и отрицательные целые; дробные делятся на положительные и отрицательные.

7.5. а) Четырехугольники делятся на выпуклые и невыпуклые. Выпуклые делятся на четырехугольники с не параллельными сторонами, трапеции и параллелограммы и т. д.

б) Два угла можно классифицировать по равенству, по наличию общей вершины, те в свою очередь - на вертикальные, смежные и на не вертикальные и не смежные.

7.6. а) Окружности, касающиеся всех сторон треугольников или их продолжений, окружности, проходящие через все вершины треугольника (описанная), и окружности, пересекающие стороны треугольника или их продолжение. Первые в свою очередь делятся на вписанные и на вневписанные (касающиеся одной стороны треугольника и продолжений двух других сторон).

б) Углы с вершиной в центре окружности - центральные; углы с вершиной внутри окружности, но не в центре; углы, вершина которых лежит на окружности, вписанные; углы с вершиной вне круга: 1) углы, одна сторона которых является касательной к окружности, а другая - секущей; 2) углы, обе стороны которых являются касательными к окружности; 3) углы, обе стороны которых секущие; 4) углы, одна или обе стороны которых находятся вне окружности.

в) Окружности, находящиеся одна вне другой; внешним образом касающиеся; пересекающиеся; внутренним образом касающиеся; одна внутри другой: 1) центры разные; 2) общий центр - концентрические.

г) Прямая вне окружности; касательная к окружности; секущая.

д) Квадратные уравнения: полные (а≠1); приведенные (а=1); неполные: без свободного члена; без среднего члена; без свободного и среднею членов.

е) Имеющие одно решение; имеющие бесконечное множество решений; не имеющие решений.

8.1. Условия: а) 1) Путешественник проехал автобусом и по железной дороге 600 км. Два объекта: путь автобусом и путь по железной дороге; отношение - их сумма равна 600. 2) Автобусом он проехал в 4 раза меньше, чем по железной дороге. Два тех' же объекта. Отношение - частное равно 4. 3) Скорость автобуса 30 км/ч. Один объект - скорость, характеристика - 30 км/ч. 4) Скорость по железной дороге 32 км/ч. Один объект - скорость, характеристика - 32 км/ч.

б) 1) ABCD - трапеция. Один объект, характеристика качественная; 2) Боковая сторона трапеции равна 15 см. Один объект, характеристика - 15 см; 3) Угол при большем основании 60°. Один объект, характеристика - 60°; 4) ABCD описана около круга. Два объекта - трапеция и круг; отношение: первый объект описан около второго.

8.2. а) Условия: 1) ΔАВС- равнобедренный (АС=ВС); 2) AD⊥BC, 3) BE⊥АС, 4) CF⊥AB. Требования: установить, какое из трех неравенств может быть истинным: 1) AD>AB; 2) ВЕ>АВ; 3) CF>AB.

б) Условия: 1) А=(x⁴-3x²+1):(х²-х-1).

2) B=(x-10)*(x+11).

Требование. Найти А-В.

8.3. 1-й шаг - раскрыть скобки, 2-й шаг - умножить обе части неравенства на общий знаменатель, 3-й шаг - перенести все члены с * в левую часть неравенства, а остальные - в правую часть, 4-й шаг - сделать приведение подобных членов, 5-й шаг - разделить обе части неравенства на коэффициент при x.

8.4. а) Надо использовать эвристику о разбиении сложной задачи на более простые задачи. Разбиваем задачу на три следующие: 1) найти расстояние от середины стороны АВ до MN (это средняя линия ΔABN, где BN=10 см); 2) найти расстояние от середины стороны АС до MN (средняя линия ΔACM, где СМ=8 см); 3) найти расстояние от середины ВС до MN (средняя линия трапеции, основания которой равны 10 см и 8 см).

б) Введем вспомогательные элементы: проводим из точки D середины АВDE≠AC и DF≠ВС, откладываем DE=1/2h_b, DF=1/2h_a. Тогда можно построить вспомогательные прямоугольные треугольники CDE и CDF, где CD - заданная медиана. Затем продолжаем CD и откладываем DK=CD. Через точку К проводим KA||CF и КВ||СЕ до пересечения с продолжениями CF и СЕ в точках А и В. ΔABC - искомый.

в) Искомая сумма равна сумме площадей треугольников АСВ и DEF

Площадь каждого из них равна - ab, следовательно, искомая сумма равна ab

Использована эвристика о замене данной задачи другой, ей равносильной.

г) Используем эвристику о разбиении области задачи на части. Рассматриваем решение уравнения в следующих промежутках:

1) <0. Левая часть уравнения положительна, поэтому в этом промежутке нет решений.

2)0<x<1. Преобразуем уравнение: x²+x⁸(1-x)+(1-x⁵)=0. Все слагаемые левой части положительны, поэтому нет решений.

3)x≥1. Преобразуем выражение так: x⁹(x³-1)+x⁵(x³-1)+1=0.

Ответ: уравнение не имеет решений.

д) Составляем равнение: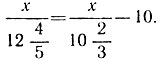

е) Заменяем данную задачу геометрической: хорды KP и LQ окружности пересекаются в точке Х. Известно, что 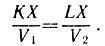Доказать, что 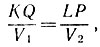где V₁ и V₂ - постоянные числа

Использованы эвристики замены и введения вспомогательных элементов.

9.1. 32 треугольника, 6 квадратов, 4 трапеции, 8 параллелограммов.

9.2. Число 16 имеет пять делителей: 1, 2, 4, 8, 16; является квадратом числа 4 и четвертой степенью числа 2; равно сумме четырех нечетных чисел: 16=1+3+5+7.

9.3. Кроме очевидных, еще такое свойство: все точки BD равноудалены от сторон АВ и ВС

9.4. 10.

9.5. Обращается в нуль при х=1 и х=-1; при -1<х<1, у<0, а при >х<-1 и x>1, у>0; при x<0 убывает, а при x>0 возрастает, при x=0 принимает наименьшее значение -1.

9.6. Сумма двух взаимно обратных чисел, которая при а>0 не меньше 2, а при а<0 не больше -2, при а=-1 равна 2, а при а=-1 равна -2.

9.7. Четное число, имеет 2(n+1) делителей, является общим членом геометрической прогрессии, первый член которой равен 6, а знаменатель равен 3.

9.8. До пункта А ученик шел с обычной скоростью 5 км/ч. Там он отдыхал 1/2 ч, а затем бежал от А до В со скоростью 12,5 км/ч. В пункте В отдыхал 2 ч. Из В в С он шел очень медленно со скоростью 2,5 км/ч. Прибыв в С, он через полчаса вспомнил, что забыл в В какую-то вещь, быстро побежал в В со скоростью 10 км/ч и сразу же вернулся в С в 17 ч.

9.9. Возможны три различных случая расположения этих точек: 1) две точки лежат на диаметре, а третья - на одной из полуокружностей; 2) все три точки лежат на одной полуокружности; 3) две точки лежат на одной полуокружности, а третья - на другой. В первом случае образуется 3 треугольника, во втором - а в третьем - 4. Кроме того, образуются секторы и сегменты круга, а во втором случае еще и четырехугольник.

10.1. а) Сходны по свойствам: пара углов; имеют общую вершину; различия: вертикальные углы всегда равны, а смежные, как правило, не равны; сумма смежных углов постоянна, а сумма вертикальных переменная, б) Сходны по свойствам: замкнутые фигуры, имеют центр симметрии. Различия: круг ограничен кривой линией, а квадрат состоит из прямолинейных отрезков; круг имеет бесконечное множество осей симметрии, а квадрат только 4 оси симметрии, в)Не сравнимы, г) Сходны по свойствам; алгебраические выражения; двучлены; суммы степеней. Различия: степени разные, д) Сходны: дроби. Различия: первое есть число, а второе - алгебраическое выражение, е) Сходны: представляют собой задачи на отыскание искомых; левые части одинаковы. Различия: первое уравнение, а второе неравенство; первое имеет лишь два корня, а второе - бесконечное множество, ж) Не сравнимы.

10.2. а), б) и г)- неверно; разные основания сравнения, в) верно, д) неверно, ибо это несравнимые объекты.

10.3. Не больше 6.

10.4. а)154,173; б) 12,19; в) 3,1; г) 125,216; д) 3; 2,5.

11.2. а) 4 мин; б) 14 м; в) 7 мин; г) 5.

11.3. а) 4; б) 2; в) 5; г) 3.

11.4. Это значит, что она обратилась к девочке.

11.5. а) 10 км; б) обе одинаково; в) в понедельник.

12.1. Потому что сразу после уроков все еще свежо в памяти и ничего не забыто, а через день-два многое забудется и труднее будет восстановить забытое.

12.2. Шпаргалки вредны тем, что используются при непонимании учебного материала. Когда материал понят, усвоен, шпаргалки не нужны. Шпаргалки дают возможность лишь механически воспроизвести непонятное и неусвоенное содержание, которое после ответа тут же исчезает из памяти, и, следовательно, при необходимости еще раз где-то использовать это содержание понадобится снова шпаргалка. Шпаргалка может "выручить" лишь для получения положительной оценки у очень невнимательного учителя. Стоит же пользующемуся шпаргалкой задать какой-то дополнительный вопрос, как сразу обнаруживается непонимание и незнание.

12.3. Да, играет, ибо хорошо и прочно запоминается лишь при установке на длительное запоминание.

12.4. Лучше всего попытаться вывести забытую формулу, тождество.

12.5. Надо запомнить метод (прием) доказательства теоремы. Дословно запоминать доказательство не следует.

13.1. 87; 101; 100; 243; 551; 393; 248; 990; 134; 186; 323; 864; 11 214.

13.2. 57; 74; 287; 166; 21; 786; 108; 756; 97; 824; 243.

13.3. 38,5; 5(13/15); 7(7/15); 9,4; 17,7; 12; 215; 414; 60; 192. 13.4.

13.4. M=160; K=11,8.

13.5. 0,25; 1,5; 2,75; 4; 5,25; 7,75; 12,75; 37,75; 51,5.

13.6. -100; 1,5; -26,4; -69; 4; -20.

13.7. а)(1/32)a²b б) 3y²; в) (b³/6-b²/8); г) а²+b²; д) -1,16+(а²-х²).

13.8. а)х=8; б) x=0,5; в) х=-12; г) x>5; д) 3<хɝ.

14.1. а) СA₁, CB₁, CD₁, СA. б) AB₁, BA_{1, AС1, СA1, CD1, DC1, DA1, AD1},

в) BD, A₁С, BC₁, DA₁.

14.2. а) 4 хода:

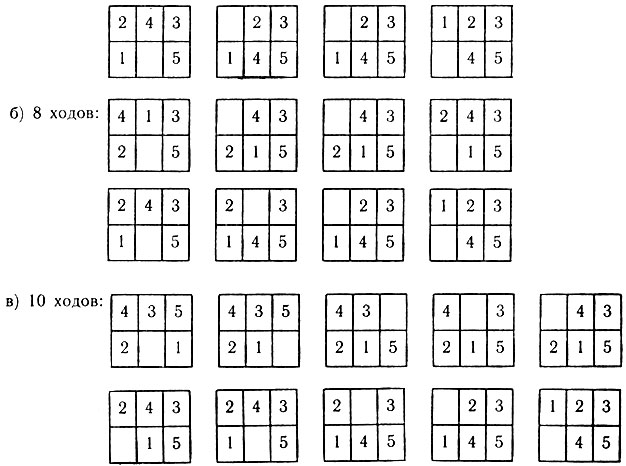
14.3. а) 6 ходов, например: с2, d4, f5, h6, f7, h8.

б) 1) b1-аЗ; b4 -а2; 2) а3-с2; а2-с3; 3) с2-b4; с3-b1;

в) 5 ходов: b3, с5, а6, с7, а8.

г) Бить пешку нельзя, 4 хода: d4, с5, f8, g7

д) 3 хода: d2, а5, с7. е) 5 ходов: f5, h3, f1, b5, с6.

15.1. Если множитель меньше 1, то произведение меньше множимого, a если множитель больше 1, то произведение больше множимого.

15.2. а) Произведение взаимно-обратных чисел равно единице.

б) При возвышении отрицательного числа в четную степень получается положительное число, а в нечетную - отрицательное число.

15.3. 3⁴²³ оканчивается на 7.

15.4. Для того чтобы узнать, делится ли число на 99, разбиваем его на грани справа налево, по две цифры в каждой грани (в последней грани может быть одна цифра), складываем полученные грани. Если эта сумма делится на 99, то и данное число делится на 99. Пример: N=2 725 668. Находим сумму: 68+56+72+2=198, эта сумма делится на 99, значит, и N делится на 99.

15.5. а) n²

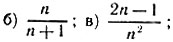
г) 0,1ⁿ; д) 3+4(n-1); е) 4-(-3)^n-1.

15.6. а) х²+у²+2ху; б) а²+b²+с²+2аb+2ас+2bс.

15.7.Через любые три точки плоскости, не лежащие на одной прямой, можно провести окружность и притом только одну.

15.8. Это уравнение означает точку (2;3) или, что то же, окружность центра (2;3) нулевого радиуса.

15.9. а) (0;-1); (-1;0); б) (0;2); (1;2); в) (-2;0); (-2;1).

15.10. Диагональ ромба делит его на два равных равнобедренных треугольника. Если равнобедренный треугольник повернуть вокруг основания, как оси вращения, до совпадения с плоскостью, то получится ромб. Следствиями свойств равнобедренного треугольника являются такие свойства ромба: диагонали ромба взаимно перпендикулярны; диагонали ромба делят углы его пополам; противоположные углы ромба равны.

а) Один комбайнер может убрать поле за 3 ч, а другой за 2 ч. За сколько времени они уберут это поле, если будут работать на нем совместно?

б) Расстояние между станциями А и В товарный поезд проходит за 3 ч, а пассажирский - за 2 ч. Из А в В вышел товарный поезд, а одновременно из В в А вышел пассажирский поезд. Через сколько времени они встретятся?

15.12. При решении уравнений. Если некоторое уравнение можно представить в виде f(х) φ (х)=0, то оно равносильно совокупности двух уравнений: f(х)=0 и φ(х)=0.

15.13. Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Так как диагонали прямоугольника равны и при пересечении делятся пополам, то отсюда следует, что медиана прямоугольного треугольника, проведенного к гипотенузе, равна ее половине. Следствием теоремы Пифагора является: сумма квадратов диагоналей прямоугольника равна сумме всех его сторон.

16.1. 5 углов.

16.2. Надо каждый из трех батонов разделить пополам, получим 6 половинок, и дать каждому по одной половинке батона. Затем каждый из оставшихся двух батонов разделить на 3 равные части, получим всего 6 третьих частей батона, и дать каждому по одной трети батона...

16.3. В 6 ч утра во вторник гусеница будет на высоте 6 м. Каждый час днем она подымается на 5/12 м следовательно, оставшиеся 3 м до вершины она проползет за 3:(5/12)=7(1/5)ч. Значит, гусеница достигнет вершины во вторник в 13 ч 12 мин.

16.4. 97 072+7843=104915 или 97 073+7842=104 915.

16.5. Обозначим число дня рождения буквой х, номер месяца - у, а число из двух последних цифр года рождения z. Тогда если вы проделаете все вычисления, то получите число: 10000x+100y+z+90 725.

Поэтому ведущий из названного результата устно отнял 90 725 и в полученной разности первые две цифры обозначают число дня рождения, следующие две - номер месяца, а последние две - последние две цифры года рождения. В приведенном примере имеем 271 194-90 725=18 04 69, что и означает 18 апреля (4-го месяца) 1969 г.

16.6. Надо отметить вершины и на сторонах еще по 2 точки.

16.7. Обозначим число бригад по сбору металлолома через х, а число учащихся в каждой бригаде - через у. Тогда получим уравнение: ху+4х=39 или (у+4)х=39. Так как 39 = 3-13, то очевидно, что х=3, у=9. Следовательно, в каждой бригаде по сбору металлолома было по 9 школьников, а по сбору макулатуры по 3 школьника.

16.8. 50 кг.

16.9. 73.

16.10. В комнате находятся внук, его отец и дед - отец отца.

16.11. |x-2|+|x-5|=3.

16.12. Трапеция; параллелограмм.

16.13. Может: они пользовались разными мерками, притом мерка Коли в 12 раз больше мерки Саши.

16.14/ Может, если высота будет равна 1 км.

16.15. Докажите методом от противного.

16.16. Допустим, что уравнение ах²+6х+с=0 (1) имеет три различных корня х₁, x₂ и x₃. Тогда справедливы следующие равенства: ах²₁+bx₁+с=0; ax²₂+bx₂+c=0; ах²₃+bx₃+с=0. Вычтем почленно из первого равенства второе, а затем третье. Получим после преобразований: (x₁-x₂)(ax₁+ax₂+b)=0, (x₁-x₃)(ax₁+ax₃+b)=0. Так как по предложению х₁-х₂≠0 и x₁-x₃≠0, то получим такие равенства: ах₁+ах₂+b =0, ах₁+ах₃+b=0.

Вычтем почленно из первого второе, получим: а(x₂-x₃)=0 x₂-x₃=0 или x₂=x₃, что противоречит предположению. Значит, оно неверно, и поэтому (1) не может иметь трех различных корней.

16.17. Так как ромб и окружность имеют центр симметрии, то при описании окружности около ромба их центры должны совпасть. Следовательно, диагонали ромба должны служить диаметрами окружности, и поэтому они должны быть равны. Но диагонали ромба, один из углов которого равен 30°, не равны. Следовательно, около такого ромба описать окружность нельзя. Обобщая, получаем такую теорему: "Если ромб не является квадратом, то около него нельзя описать окружность".

16.18. Легко доказать, что хорды, соединяющие концы двух параллельных хорд окружности, равны. Поэтому если около трапеции описана окружность, то боковые стороны трапеции равны. Следовательно, около неравнобочной трапеции описать окружность нельзя. Вписать же окружность можно, если сумма длин оснований равна сумме длин боковых сторон.

16.19. Например: 2x²+3x+5<0 или -2х²+3х-5>0.

16.20. Длины всех окружностей увеличатся на одну и ту же величину 2π м.

16.21. Пусть общая сторона этих двух прямоугольных треугольников равна h, а их гипотенузы b и с. Вторые катеты в таком случае являются проекциями b и с на сторону а. Обозначим их b₁ и c₁. Тогда имеем: b²=h²+b²₁. c²=h²+c²₁. Отсюда b²-c²=b²₁-c²₁ или (b-с)*(b+c)=(b₁-c₁)-(b₁+c₁), но b₁+c₁=a, поэтому (b+c):a=(b₁-c₁):(b-с).

16.22. Минутная стрелка прошла от начала часа угол, равный (360º*24)/60=144°, а часовая стрелка от начала дня угол (360º/12)*3(24/60)=102°. Следовательно, они образуют между собой угол в 42°.