
Занятие 5. Развивайте свое воображение и мышление
Вся математика есть результат деятельности воображения и мышления человека. Ведь математические объекты реально не существуют, их нет в природе, вокруг нас, они - плод воображения и мышления, но отражающие предельно точно этот окружающий нас мир.
В окружающем нас мире нет геометрических фигур, нет чисел и функций, нет многочленов и уравнений. Но в этом мире есть предметы, имеющие форму, есть совокупности предметов, имеющие величину и количество, происходят явления и процессы, в которых предметы находятся в каких-то меняющихся отношениях. Однако, для того чтобы отделить форму от предметов, величину и количество от их совокупности, отношения от явления и процессов и сделать эти формы, величины, количества и отношения самостоятельными объектами, нужна была огромная работа в течение тысяч лет человеческого воображения и мышления.
Поэтому и изучение математики, овладение ею требует развитого воображения и мышления. Нужно упорно учиться видеть и действовать в уме. Учитель говорит: "Если повернуть параллелограмм вокруг точки пересечения диагоналей на 180°, то, как вы думаете, совпадает ли он со своим первоначальным положением?". Чтобы правильно ответить на этот вопрос, мы должны мысленно представить себе то, о чем говорил учитель: увидеть параллелограмм с диагоналями, увидеть процесс его поворота вокруг точки пересечения диагоналей, и тогда вы сможете точно, а не наугад ответить на заданный вопрос. Вы читаете в учебнике: "В ΔABC проведены из вершины С высота, биссектриса и медиана". И вы должны вообразить этот треугольник AВС, увидеть, что его стороны АС и СВ не равны, ибо в противном случае высота, биссектриса и медиана просто слились бы, увидеть, что высота проходит ближе к меньшей стороне, а биссектриса и медиана - ближе к большей стороне, но вот неясно, проходит ли биссектриса между высотой и медианой или же медиана между высотой и биссектрисой. Это уже требует особого исследования.
Однако надо не только видеть в уме услышанное или прочитанное, но надо уметь и действовать в уме. Вам надо разделить 235 698 на 2. Неужели вы будете это делать углом? Нет, вы должны сразу писать ответ, выполняя все промежуточные действия в уме. Или вам надо преобразовать алгебраическое выражение, уравнение, неравенство. И опять-таки многие промежуточные преобразования надо выполнять в уме, устно.
Умение видеть и действовать в уме особенно вам понадобится, когда вы начнете изучать стереометрию - геометрию в пространстве. Ведь бумага, на которой вы можете чертить, изображать изучаемые в стереометрии пространственные фигуры, плоская. Поэтому без воображения, без умения видеть и действовать в уме вы не сможете понять никакой чертеж, никакое изображение пространственных фигур. С необходимостью видеть и действовать в уме вы встретитесь и на любой работе. Токарь, слесарь, конструктор, технолог, архитектор, строитель должны уметь по плоскому чертежу увидеть сложную пространственную деталь, сооружение или машину. Геолог, географ, военный, агроном должны уметь по карте или плану увидеть все особенности местности, сориентироваться на ней. Для того чтобы разумно выполнить некоторую работу, надо предварительно ее спланировать, "проиграть" в уме, а уже затем начать действовать.
Математика изучает общие свойства бесконечных совокупностей математических объектов. Когда вы доказали, что сумма углов треугольника равна 180°, то тем самым вы установили, что этим свойством обладает любой треугольник, а их бесконечное множество. Но чтобы это свойство установить, надо было сначала его заметить, сформулировать и уже потом доказать. Человечество приходило к математическим истинам не сразу, а постепенно, замечая свойства отдельных объектов, а затем обобщая их. Еще древние египтяне знали, что треугольник со сторонами 3, 4 и 5 прямоугольный, и пользовались этим для построения прямого угла на местности. Но прошло много сотен лет, пока это частное свойство одного треугольника было обобщено для любых прямоугольных треугольников и была доказана теорема, обратная теореме Пифагора.
Значит, важно учиться обобщать единичные факты, наблюдения. Вот вы наблюдаете такие факты: 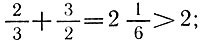 ;
;
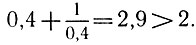
И из этих наблюдений вы должны суметь сделать такое обобщение:
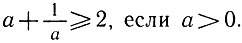
Конечно, это обобщение затем надо будет доказать.
Здесь проявляется ваша сообразительность, умение делать догадки. А ведь сообразительность и основана на умении видеть общее в частном, видеть сходство в различном. Какая связь, например, между медианой треугольника и диагональю параллелограмма?
На первый взгляд, кажется, что никакой. А связь есть, и весьма непосредственная. Продолжите медиану CD ΔAВС на ее длину (DE=CD) и соедините полученную точку Е с вершинами А и В. Получите параллелограмм АСВЕ, в котором медиана CD является половиной диагонали СЕ.
Значит, для того чтобы успешно учиться математике, овладевать ею, вам надо развивать свое воображение и мышление, упорно учиться видеть и действовать в уме, обобщать и догадываться, развивать свою сообразительность. Что для этого нужно делать? Нужна упорная и терпеливая работа над собой, нужно проявлять волю и настойчивость в преодолении трудностей, возникающих в процессе учения. Если решаете задачу, то решайте ее самостоятельно, и если она не "выходит", то имейте терпение посидеть над нею и, может быть, не один день, но добейтесь и найдите ее решение. Критически анализируйте свои качества, свои умения, не стесняйтесь признаваться, что вы еще что-то не знаете, что-то не умеете, что у вас то или иное качество недостаточно развито, и упорно работайте над собой, чтобы развить это качество, овладеть этим умением, этим знанием.
И пожалуйста, не ссылайтесь на то, что у вас нет способностей к математике. Вы должны сами работать над собой. Здесь уместно напомнить изречение основоположника итальянской компартии Антонио Грамши (1891 -1937), что человек сам творит себя, хотя и в зависимости от условий общества, своего положения в нем, полученного воспитания. Человек - это процесс его собственных действий, производимых по его собственной воле.
Итак, работайте над собой. Приводим некоторые из задач, которые можно использовать для развития и тренировки указанных качеств.
Задание 13
13.1. Выполните устно следующие действия: 56+13+ 18; 24+16+14+47; 39+48+13; 326-83; 624-73; 516-123; 31-8; 165*6; 536:4; 1488:8; 17*19; 72*12; 145 782:13.
13.2 Попросите кого-либо, чтобы вам продиктовали следующие примеры, которые решите устно, записывая лишь ответ: 16+23+18; 34+17+23; 263+24; 89+77; 87-42+14-38; 881-95; 18*6; 108*7; 485:5; 2472:3; 35.
13.3. Решите устно следующие примеры: 23,8+14,7;2(1/5)+3(2/3);4(3/4)+2(5/6); 18,7-9,3; 37,2-19,5; 3(1/5)*3(3/4); найти: 5/8 от 344; 2/5 от 1035; 75% от 80; 15% от 1280.
13.4. Вычислите устно:
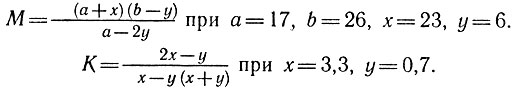
13.5. Составьте таблицу значений функции 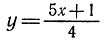 при х=0; 1; 2; 3; 4; 6; 10; 30; 41.
при х=0; 1; 2; 3; 4; 6; 10; 30; 41.
13.6. Вычислите устно:
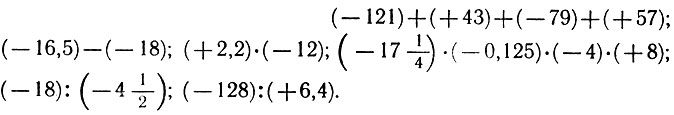
13.7. Выполните устно приведение подобных членов:
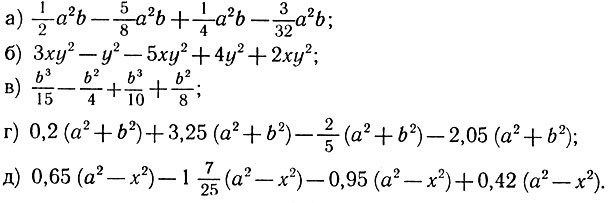
13.8. Решите устно уравнения и неравенства:
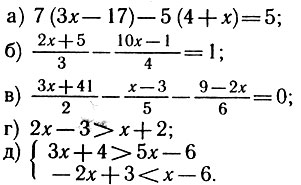
Задание 14
14.1. Представьте себе куб, вершины нижнего основания которого обозначены в порядке движения против часовой стрелки A, В, С и D, а соответствующие вершины верхнего основания А1, В1, С1 и D1. Назовите, не глядя на чертеж: а) диагональ куба и диагонали граней куба, выходящие из вершины С; б) диагонали всех боковых граней куба; в) в передней грани проведена диагональ АВ1. Какие диагонали смежных граней не пересекаются с данной диагональю?
14.2. Игра в "пять".
На шести расположенных в два ряда клетках в произвольном порядке размещены пять перенумерованных фишек. Например:
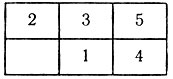
За один ход можно передвинуть в свободную клетку одну из фишек, стоящую рядом по горизонтали или вертикали. Игра состоит в том, чтобы за наименьшее число ходов перейти от исходного расположения фишек к заданному конечному расположению:
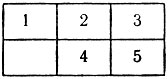
В данном случае задача решается за 6 ходов:
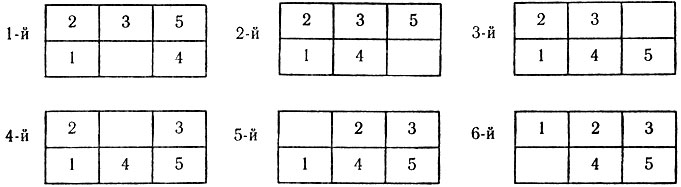
Решите задачи этой игры для следующих начальных расположений фишек:

14.3. Вообразите шахматную доску. Как вы знаете, она представляет собой квадрат, разбитый на 8*8=64 клетки - поля доски. Вертикали доски (слева направо) обозначаются буквами а, b, с, d, е, f, g, h, а горизонтали (снизу вверх) - числами 1, 2, 3, 4, 5, 6, 7, 8. Поэтому каждое поле шахматной доски обозначается двумя знаками: буквой и числом. Так, самое левое нижнее поле обозначается a1, а самое правое верхнее -h8.
Решите мысленно, без фигур, не глядя на доску, следующие задачи, записывая лишь на бумаге ваши ходы:
а) Конь занимает поле a1. Через какие поля он должен ходить, чтобы за наименьшее число ходов перейти на поле h8?
б) Белый конь находится на поле b1, а черный - на поле b4. Как им поменяться местами, не оказавшись ни разу под боем?
в) Как должен ходить конь, чтобы с поля a1 перейти на поле а8?
г) Белый слон находится на поле a1, а черная неподвижная пешка - на поле f6. Как должен ходить слон, чтобы оказаться на поле g7?
д) Белый слон находится на поле с1, а черный неподвижный ферзь - на поле f6. Как должен ходить слон, чтобы оказаться на поле с7?
е) Белый слон находится на поле b1, а неподвижные черные ферзь и ладья находятся на полях g7 и d4. Какие ходы должен сделать слон, чтобы попасть на поле с6?
Задание 15
15.1. Какой общий вывод относительно произведения можно сделать на основе следующих примеров:
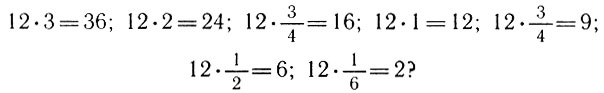
15.2. Обобщите следующие примеры:
a)6*(1/6)=6; (2/3)*(3/2)=1; б)(-4)2=16; (-4)3=-64.
15.3. Заметьте, что 31=3, 32=9, 33=27, 34=81. На какую цифру оканчивается число 3423?
15.4. Известен следующий признак делимости на 9: если сумма цифр n числа делится на 9, то и само число делится на 9. Догадайтесь, каков признак делимости на 99.
15.5. Напишите общую формулу n-го члена следующих последовательностей: а) 1, 4, 9, 16 ...
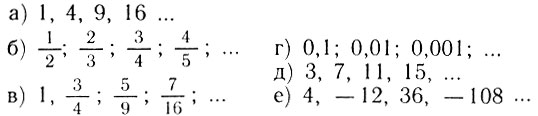
15.6. Вы знаете, что (a+b)2=a2+b2+2ab. Напишите, чему равно следующее выражение, выполняя все промежуточные преобразования устно: а) (-x-y)2; б) 392; в) (а+b+с)2.
15.7. Имеется теорема: "Около любого треугольника можно описать окружность, и притом только одну". Как иначе можно сформулировать эту теорему?
15.8. Общее уравнение окружности (х-х0)2+(у-у0)2-с2, где (х0, у0) - координаты центра окружности, а r - радиус окружности. Каков геометрический смысл уравнения (х-2)2+(y-3)2=0?
15.9. По уравнению прямой написать координаты каких-либо двух ее точек: а) -х-у= 1; б)у = 2; в)х=-2.
15.10. Какая связь между равнобедренным треугольником и ромбом? Какие свойства ромба являются следствиями свойств равнобедренного треугольника?
15.11. Дана задача: "Через первый кран ванна наполняется за 3 ч, а через второй - за 2 ч. За сколько времени наполнится ванна, если открыть одновременно оба крана?" Составьте задачи, аналогичные данной, чтобы в них шла речь: а) о работе комбайнеров; б) о движении поездов.
15.12. Известно, что если ab=0, то а или b либо а и b одновременно равны нулю. Где и как используется это свойство?
15.13. Какая связь между прямоугольным треугольником и прямоугольником? Какое свойство медианы прямоугольного треугольника следует из свойств прямоугольника? Какое свойство прямоугольника следует из свойств прямоугольного треугольника?
Задание 16
16.1. Крышка стола имеет 4 угла. Если один из углов отпилить, то сколько станет у крышки углов?
16.2. Разделить 5 батонов хлеба между 6 человеками, не разрезая ни один батон на 6 равных частей.
16.3. Гусеница за день вползает вверх по дереву на 5 м, а за ночь спускается на 2 м. Если она начала вползать на 9-метровое дерево в воскресенье в 6 ч утра, то когда она достигнет вершины?
16.4. Расшифруйте действие: 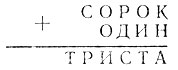
16.5. На математическом вечере ведущий объявил: "Кто желает проверить, что я могу угадать дату вашего рождения, возьмите листочек бумаги и произведите следующие действия: число дня вашего рождения умножьте на 20 и прибавьте 180. Сумму умножьте на 5 и прибавьте число месяца рождения. Умножьте эту сумму на 20 и прибавьте 145, результат умножьте на 5 и прибавьте число из двух последних цифр года вашего рождения. Назовите конечный результат, и я скажу дату вашего рождения". Один из участников назвал результат: 271 194. Ведущий ему сказал: "Вы родились 18 апреля 1969 г.". Как он это угадал?
16.6. Как отметить на сторонах прямоугольника 12 точек, чтобы на каждой стороне было отмечено 4 точки?
16.7. 39 школьников класса были распределены на несколько бригад по сбору металлолома и 4 бригады по сбору макулатуры с таким числом школьников в каждой, сколько бригад по сбору металлолома. Сколько школьников в каждой бригаде по сбору металлолома и по сбору макулатуры?
16.8. На склад поступило 100 кг грибов. Проведенный анализ показал, что в грибах имеется 99% воды. Через некоторое время анализ повторили. Оказалось, что содержание воды уменьшилось до 98%. Какова теперь масса грибов?
16.9. Внук спросил бабушку: "Сколько тебе лет?" Она ответила: "Каждая из двух цифр в числе моих лет равна возрасту твоих двоюродных братьев Коли и Саши".- "Но я не знаю, сколько им лет",- возразил внук. "Если ты сложишь вместе возраст Коли, Саши и мой, то получится 83". Сколько лет бабушке?
16.10. В комнате находятся два отца, два сына, дед да внук, а всего трое. Как это может быть?
16.11. Придумайте уравнение, корнями которого являются все числа от 2 до 5.
16.12. Что это за четырехугольник, у которого диагональ перпендикулярна двум неравным сторонам? А если эта диагональ перпендикулярна двум равным сторонам?
16.13. Саша и Коля измерили расстояние между точками A, В, С. Саша сказал: "AB=1, ВС=2,5", а Коля сказал: "АВ=12, ВС=30". Оба мальчика утверждали, что они произвели измерение правильно. Может ли это быть?
16.14. Основание треугольника равно 1 мм. Может ли его площадь быть равной 1 м2?
16.15. Докажите, что биссектриса разностороннего треугольника не может быть перпендикулярна стороне треугольника.
16.16. Докажите, что квадратное уравнение не может иметь три различных корня.
16.17. Докажите, что если один из углов ромба равен 30° то его нельзя вписать в окружность. Сформулируйте эту теорему в общем виде.
16.18. Докажите, что если трапеция не равнобочная, то вокруг нее нельзя описать окружность. А можно ли в нее вписать окружность?
16.19. Напишите квадратное неравенство, которое не имеет решений.
16.20. Радиусы трех окружностей 1 м, 10 м и 10 000 м. Радиус каждой окружности увеличили на 1 м. Длина какой окружности увеличится при этом больше других?
16.21. Любой остроугольный треугольник можно образовать из двух прямоугольных треугольников. Докажите, что сумма двух сторон такого треугольника так относится к третьей, как разность проекций первых двух сторон на третью относится к разности этих сторон.
16.22. Какой угол образует между собой часовая и минутная стрелки часов в 3 ч 24 мин?
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'