Занятие 2. Учитесь сравнивать

Должно быть, все вы не раз слышали крылатую фразу: "Все познается в сравнении". И действительно, оценить что-либо, установить, чем оно является, хорошо это или плохо, каков данный объект, можно, лишь сравнивая его с каким-либо другим. Я показываю вам карандаш и спрашиваю: большой он или маленький? Вы мне, очевидно, скажете:

- А по сравнению с чем? По сравнению с одним предметом он большой, а по сравнению с другим - он маленький.

Если я вам покажу несколько предметов и спрошу: какой из них самый большой, то вы вправе мне сказать, что вопрос поставлен неверно, он бессмысленный. Ведь не сказано, по какому свойству (признаку, параметру) надо установить наибольший предмет: по длине, по объему, по массе или еще по какому-либо параметру.

Вообще сравнивать предметы можно лишь по определенному общему свойству (признаку, параметру).

Если это свойство не указано, то вопрос о сравнении предметов не имеет смысла, сравнение невозможно.

Значит, для того чтобы сравнить предметы, объекты, надо сначала выявить их общие свойства, а лишь затем установить, по каким свойствам эти предметы сходны (одинаковы, равны), а по каким они различны (неодинаковы). Если же объекты таковы, что они вообще не имеют общих свойств, то их и сравнивать нельзя. Например, треугольник и многочлен не имеют, видимо, каких-либо общих свойств, а поэтому их и сравнивать нельзя. Треугольник можно сравнить с другим треугольником, с многоугольником, многочлен можно сравнить с другим многочленом, но между собой треугольник и многочлен сравнивать нет смысла.

А сравнивать математические объекты нужно, ибо только в сравнении мы познаем их наиболее важные свойства, изучаем их. Сравнивая треугольники между собой, мы устанавливаем, какие виды треугольников могут быть, сравнивая их с другими геометрическими фигурами, мы выявляем их особые свойства, например их жесткость: из трех отрезков можно образовать один и только один треугольник (если, конечно, эти отрезки удовлетворяют соотношению, что каждый из них меньше суммы двух других), а вот из четырех отрезков можно образовать не один четырехугольник, а много различных. Свойство жесткости треугольников очень важное, оно широко применяется в технике, в строительстве.

Поэтому вполне прав поэт Р. Сеф, который в шутливой форме писал:

Кто ничего,
Не замечает,
Тот ничего, 
Не изучает.
Кто ничего 
Не замечает,
Тот вечно хнычет 
И скучает.

Сравним, например, медиану и биссектрису треугольника. Обе они являются отрезками, обе они соединяют вершину треугольника с какой-то точкой противоположной стороны, но медиана делит эту сторону пополам, а биссектриса делит угол при вершине пополам. Сравним теперь медиану и высоту треугольника. Они более резко различаются между собой, чем медиана и биссектриса. Это проявляется хотя бы в том, что медиана и биссектриса всегда находятся внутри треугольника, а высота может проходить и вне его.

Посмотрите на числа 4, 16, 38, 10. Сравните их, что в них общего? Пожалуй, лишь то, что все они натуральные числа и все четные. А вот числа 1, 4, 9, 16, 25, 36 имеют более существенное общее свойство: все они представляют собой квадраты последовательных натуральных чисел. Поэтому если нужно продолжить первую последовательность чисел, то после 10 можно поставить любое четное число, а вот во второй после 36 можно поставить лишь 49, затем 64, с тем чтобы сохранить замеченное общее свойство (закономерность) этих чисел.

Выявить общее свойство данных объектов не всегда легко. Например, по какому общему свойству (закономерности) написана следующая последовательность чисел: 16, 12, 15, 11, 14, 10?

Сравнивая эти числа попарно, замечаем: 16-4=12, 12+3=15, 15-4=11, 11+3=14, 14-4=10.

Значит, числа этой последовательности составлены так, что последующее число получается из предыдущего попеременно то вычитанием 4, то прибавлением 3. Поэтому если надо приписать к ней еще два числа, то можно написать такие числа: 10+3=13 и 13-4=9.

Но можно заметить и такое общее свойство чисел этой последовательности: она составлена из двух очень простых последовательностей: 16, 15, 14 и 12, 11, 10, причем члены второй последовательности расставлены между членами первой. Значит, чтобы приписать еще два числа к этой последовательности, продолжаем каждую из составляющих: 16, 15, 14, 13 и 12, 11, 10,9 - и затем члены второй последовательности расставляем между членами первой: 16, 12, 15, 11, 14, 10, 13, 9.

Для нахождения общего свойства членов последовательности нам пришлось сравнивать между собой числа. Как известно, для сравнения чисел существуют два основных способа: разностное и кратное сравнение. При разностном сравнении мы находим разность этих чисел и по ней судим, какие из данных чисел больше, а какие меньше и на сколько. При кратном сравнении положительных чисел мы находим их частное и по нему в зависимости от того, больше оно или меньше 1, судим, какое из данных чисел больше, а какое меньше и во сколько раз.

Так, сравнивая разностным способом числа 4 и 12, находим, что 12-4 = 8, Это значит, что 12 больше 4 на 8 или 4 меньше 12 на 8. Сравнивая эти же числа кратным способом, находим, что 4:12=1/3 или 12:4=3. Это значит, что 4 меньше 12 в 3 раза или составляет 1/3 от 12, а 12 больше 4 в 3 раза.

Вы хорошо знаете способ сравнения отрезков путем непосредственного наложения их друг на друга. Точно так же путем наложения можно сравнивать углы. В результате такого непосредственного сравнения числа, отрезки, углы можно расположить по порядку возрастания или убывания. Точно так же можно сравнивать между собой квадраты, круги. А вот уже прямоугольники так сравнивать нельзя. Для их сравнения, так же как и для сравнения других фигур, в математике разработан метод опосредственного сравнения с помощью измерения.

Для этого сравниваемые объекты измеряют с помощью одной и той же единицы измерения, а затем сравнивают полученные числа. Так, для сравнения двух прямоугольников по площади их измеряют с помощью единицы измерения - квадрата - со стороной, равной единице длины, после чего остается сравнить полученные числа.

Эти два способа сравнения однородных объектов можно наглядно увидеть при нахождении массы тела. Когда мы сравниваем два предмета с помощью чашечных весов без гирь, то это способ непосредственного сравнения; когда же для сравнения этих же предметов их взвешивают на весах с помощью гирь,т. е. находят численную величину их массы, а затем сравнивают полученные числа, то это уже способ опосредственного сравнения.

Заметим, что два объекта можно сравнивать не по одному какому-то свойству (признаку), а, как правило, по разным и многим признакам (основаниям сравнения). Например, треугольники можно сравнивать по площади, по периметру, по виду углов (сравниваемые треугольники могут быть оба остроугольными или один из них остроугольный, а другой тупоугольный и т. д.), по соотношению сторон (например, один из них равнобедренный и т. д.) и еще по другим основаниям.

Сложнее сравнивать алгебраические объекты: многочлены, уравнения, тождества, функции и т. д. Так, сравнивая между собой многочлены, можно лишь установить, различаются ли они по числу переменных или по наивысшей степени переменных. Можно, конечно, их сравнить и по тому, какие буквы входят в эти многочлены: одни и те же или разные. Но это различие не-существенное, ибо, например, многочлены х²+ху+у² и а²+ab+b² существенно не различаются: по сути дела это один и тот же многочлен.

Как видим, сравнение лежит в основе классификации объектов, а измерение есть способ сравнения, и в то же время само измерение производится с помощью сравнения измеряемого объекта с единицей измерения.

В основе решения большинства задач также лежит сравнение. А многие задачи прямо связаны со сравнением. Вот пример такой задачи.

Задача.Хорда АВ окружности, не проходящая через центр, разделена пополам в точке М. Докажите, что любая другая хорда, проходящая через точку М, больше хорды АВ.

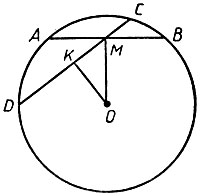
Рис. 23

Решение. В данном случае мы не можем непосредственно сравнить отрезки АВ и CD произвольной хорды, проходящей через точку М, путем наложения одного их этих отрезков на другой (рис. 24). Значит, нам нужно их сравнить опосредственно. Как же это можно сделать? Способ измерения здесь не под-ходит, ибо мы должны сравнить отрезок АВ не с одним каким-то определенным отрезком, а с любым, являющимся хордой окружности, проходящей через точку М. Значит, мы должны использовать какие-то теоремы о сравнении отрезков. Какие теоремы такого характера мы знаем? Имеются теоремы о сравнении сторон треугольников, например что в треугольнике против большего угла лежит и большая сторона. Но в данном случае нам нужно сравнить не просто отрезки, а хорды окружности. А что мы о них знаем? Вспоминаем такое их свойство: чем хорда окружности ближе к центру, тем она больше. Тогда найдем расстояние сравниваемых хорд АВ и CD до центра О. Для этого из О опускаем перпендикуляры на АВ и CD. Как известно, эти перпендикуляры проходят через середины хорд. Значит, ОM ⊥АВ и OK⊥CD. Рассматривая полученный прямоугольный треугольник ОМК, находим, что ОК<ОМ, ибо катет меньше гипотенузы. Следовательно, CD>AB, что и требовалось доказать.

Когда надо сравнить более двух объектов, то можно либо непосредственно сравнивать их попарно, либо заменить их такими объектами, сравнение которых осуществить просто и легко.

Например, нужно сравнить по росту трех учеников А, В и С. Можно это сделать двумя способами.

1-й способ. 1) Сравним непосредственно А и В (ставим их спиной друг к другу и видим, кто из них выше). Пусть А<В.

2) Сравниваем также В и С. Если В<С, то получаем: А<В<С. Если же В>С, то приходится произвести еще один шаг.

3) Сравниваем A и С. Если А<С, то получаем: A<С<В, если же А>С, то С<А<В.

2-й способ. Измеряем рост всех трех учеников, допустим, получили: A=158, В=160, С=156. Осталось сравнить числа 158, 160 и 156. Это сделать легко, получаем: 156<158<160, следовательно: С<A<В.

10.1. Сравните следующие пары математических объектов, укажите, по каким признакам (свойствам) они сходны, а по каким различны:

а) вертикальные и смежные углы;

б) круг и квадрат;

в) линейное уравнение и параллелограмм;

г)a²+b² и x³+у³;

д)3/4 и (a-1)/(a+2)

е)x²-5x+6=0 и x²-5x+6>0

ж) прямоугольный треугольник и функцию у=х².

10.2. Верно ли произведено сравнение объектов, а если неверно, то в чем ошибка:

а) Сравнив треугольники ABC и MKL, установили, что ΔABC - прямоугольный, а ΔMKL - равнобедренный.

б) Сравнив два прямоугольника, установили, что один из них имеет площадь 48 м², а периметр другого равен 60 м.

в) Сравнив два круга, установили, что радиус одного из них равен 6 м, а радиус другого 8 м.

г) Сравнили два многочлена и установили, что степень первого из них равна трем, а второй есть сумма трех одночленов.

д) Сравнили треугольник ABC и многочлен М и установили, что площадь ΔАВС равна 10 м², а значение многочлена М при х=2 равно 10.

10.3. 4 различных по массе предмета требуется расположить в порядке убывания их масс. Пользоваться для этого можно лишь чашечными весами без гирь. Сколько взвешиваний достаточно для решения этой задачи?

10.4. Найдите общее свойство в следующих последовательностях чисел и допишите в каждой из них еще по два числа:

а) 82, 97, 114, 133...

б) 15, 16, 14, 17, 13, 18...

в) 9, 1, 7, 1, 5, 1...

г) 1, 8, 27, 64...

д) 66, 34, 18, 10, 6, 4...