
Занятие 1. Учитесь видеть, наблюдать
Чтобы успешно учиться математике, прочно ею овладеть, надо, конечно, обладать некоторыми общими умениями и качествами. Нужно уметь видеть объекты во всем многообразии их свойств и отношений, уметь сравнивать эти объекты, находить черты сходства и различий, уметь действовать в уме, представлять мысленно любые объекты и видеть в уме все их особенности и изменения при тех или иных преобразованиях, т. е. иметь хорошо развитое воображение. Конечно, надо обладать также достаточной волей и вниманием, хорошей памятью, сообразительностью.
Но разве всеми этими умениями и качествами не нужно обладать, чтобы успешно учиться по другим предметам, чтобы в будущем хорошо трудиться, работать на производстве, в колхозе?.. Так что в этом отношении математика ничем особенным не отличается от других предметов. Кроме того, разве каждый из вас не хочет, чтобы у него была хорошая память, развитое воображение, внимание, крепкая воля, сообразительность, умение наблюдать и обобщать и т. д. независимо от того, нужно ли все это для изучения математики или не нужно? Не сомневаюсь, что все вы хотите этого. Так давайте будем развивать свои умения, качества своего ума!
Учтите очень важное положение: все названные мною умения и качества нужны для изучения математики, без них оно не может быть успешным, но сами умения и качества развиваются и крепнут в процессе упорного, плодотворного изучения математики.
Тут диалектика: для того чтобы учиться, нужны умения и особые качества ума, а эти умения и качества развиваются, формируются в процессе учения.
Если вы внимательно и активно будете участвовать (а не только присутствовать) на наших занятиях, если вы проделаете все упражнения, все задания, которые я вам буду задавать, то уверена, что вы сами почувствуете пользу наших занятий для себя.
Итак, начнем первое занятие. Будем учиться видеть, наблюдать. Ведь можно смотреть и мало видеть, а надо научиться не просто смотреть,- это вы умеете,- а видеть встречающиеся вам объекты во всем их многообразии свойств и отношений.
Вы уже знаете, что каждый математический объект имеет очень много различных свойств. Но при определении этих объектов указывают лишь самые существенные свойства, необходимые и достаточные для их распознания.
Возьмем такой пример. Средняя линия треугольника определяется как отрезок, соединяющий середины двух сторон треугольника. Рассмотрим треугольник ABC и среднюю линию EF в нем (рис. 18). Какими свойствами обладает EF?
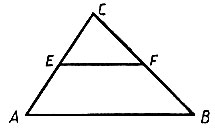
Рис. 18
- EF - отрезок... средняя линия треугольника ABC... параллельна AB...EF равна половине стороны АВ...
- Все это верно, это все вытекает из определения средней линии и из известного свойства. А еще какие свойства А EF вы видите?.. Больше не видите?
А ведь EF обладает еще многими другими свойствами. Вот некоторые из них: EF - сторона треугольника EFC и она меньшее основание трапеции ABEF; EF - сторона углов EFC, EFB, FEA и CEF. EF делит треугольник на две части, притом площадь верхней части составляет одну четверть площади всего треугольника, и т. д.
Как видите, этот простой математический объект, кроме свойств, указанных в определении и теоремах, обладает еще многими другими свойствами. Надо учиться их замечать, видеть, ибо без этого, без такого многообразного взгляда на математические объекты, вы не сумеете решать математические задачи, доказывать теоремы.
Возьмем теперь число 144. Какими свойствами оно обладает?
- Это натуральное число... Оно четное, делится на 3... 144 - это квадрат 12...
- Верно. Но это число обладает еще многими другими свойствами. Оно делится не только на 2 и на 3, а на многие другие числа. Вот все делители числа 144: 1 и 144; 2 и 72; 3 и 48; 4 и 36; 6 и 24; 8 и 18; 12 - всего 13 делителей.
Это число обладает еще и тем свойством, что оно делится на сумму своих цифр 144: (1+4+4)= 16, а 16 есть произведение этих цифр:16=1*4*4. Значит, оно делится и на произведение своих цифр. Если поменять местами первую и последнюю цифры этого числа, то получим 441, а это есть квадрат числа 21, получаемого переменой мест цифр числа 12.
Обычно в математике объекты рассматривают относительно друг друга, так же как в жизни. Отрезок EF становится средней линией, если он проведен соответствующим образом в треугольнике, а сам по себе он просто отрезок.
Посмотрите на чертеж (рис. 19). На этом чертеже изображена прямая АВ, перпендикулярная к прямой АС, и ВС - наклонная к этой же прямой. Но та же прямая АВ является наклонной к прямой ВС, а сама АС перпендикулярна АВ и наклонная к ВС. Таким образом, одна и та же прямая может быть перпендикулярной к одной прямой и наклонной к другой.
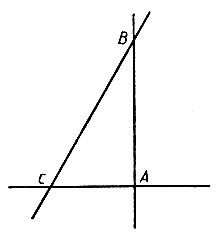
Рис. 19
Если объект сложный, то, рассматривая его, изучая, надо уметь все правильно схватить, увидеть все его особенности. Для этого сам процесс рассмотрения надо производить в определенном порядке, а не хаотично. А то может произойти то, что произошло с мальчиком Лемеле в стихотворении Льва Квитко:
Мама сказала: - Ты мне услужи, Сестру уложи, Дрова наколоть Не забудь, мой сынок, Поймай петуха И запри на замок. Сестренка, тарелки, Петух и дрова... У Лемеле только Одна голова! - Схватил он сестренку И запер в сарай. Сказал он сестренке: - Ты здесь поиграй! Дрова он усердно Помыл кипятком, Четыре тарелки Разбил молотком. Но долго пришлось С петухом воевать: Ему не хотелось Ложиться в кровать.
Посмотрите на чертеж (рис. 20). Сколько на нем изображено треугольников? Рассматривая внимательно чертеж слева направо, находим всего 15 треугольников: АОЕ, ОЕН, ОЕР, ЕНР, EBL, ЕМВ, ЕКМ, EKL, KFR, KML, KBL, RMQ, RCB, QLC, PBN.
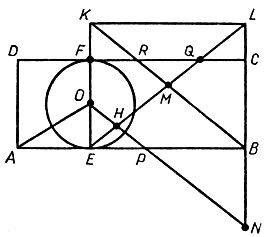
Рис. 20
А сколько там изображено различных четырехугольников? Находим 5 прямоугольников: AEFD, ABCD, EBCF, EBLK, FCLK один параллелограмм - ONBE; 8 трапеций: AOFD, ОНМК, НРВМ, HNBM, KRQL, EBCQ, KRCL, KFQL; 2 неправильных четырехугольника - AOHE и MBCQ и, наконец, один пятиугольник OHMRF.
А еще там имеется окружность центра О с диаметром с двумя другими радиусами, с несколькими секторами, сегментами. Как видим, какое богатство различных фигур мы обнаруживаем при внимательном рассмотрении этого незамысловатого чертежа.
Еще пример. Дано алгебраическое выражение:
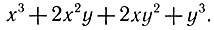
Что вы о нем можете сказать?
Это многочлен... Третьей степени... В нем четыре члена...
Его можно разложить на множители: x3+2x2y+2xy2+y3=(x3+y3)+(2x3 + 2xy2)=(x+y)*(x2+xy+y2)
Все верно, молодцы. Но вот самое простейшее, но очень важное свойство вы не заметили. Ведь этот многочлен не меняется при замене х на у и обратно у на x. Действительно, получим: y3+2y2x+2yx2+x3, т. е. тот же многочлен, но его члены написаны в обратном порядке. Еще одно важное свойство вы не заметили: коэффициенты членов, одинаково удаленных от начала и конца многочлена, равны: 1, 2, 2, 1.
Наконец, что вы можете сказать о функции, график которой изображен на чертеже (рис. 21)?
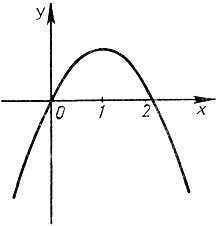
Рис. 21
- Это парабола...
- Да, это парабола. Но я спрашиваю не о кривой, а о свойствах функции, графиком которой является данная парабола.
- Это график квадратного трехчлена...
- Эта функция при х=0 и при х=2 обращается в нуль...
Маловато вы увидели... А ведь по графику можно многое установить относительно изображаемой функции... Раз это парабола, то функция квадратичная, которая в точках 0 и 2 обращается в нуль. Обратите внимание: ветки параболы направлены вниз - это значит, что коэффициент старшего члена квадратичной функции отрицательный. Поэтому эта функция такая: y=-x(x-2)=2x-x2. По графику видно, что эта функция при х<0 возрастает, при х=1 она принимает наибольшее значение (максимум), равный, как легко видно, 1 и при x>2 убывает. Значения этой функции при х<0 и при х>2 отрицательны, а при 0<х<2 - положительны.
Итак, вы видите, что каждый математический объект обладает многими свойствами, и надо уметь видеть эти свойства. Для этого следует тренироваться в подобных наблюдениях, с этой целью дома выполните следующее задание.
Задание 9
9.1. Сколько треугольников на чертеже (рис. 22)? А сколько квадратов? Какие еще фигуры имеются на этом чертеже?
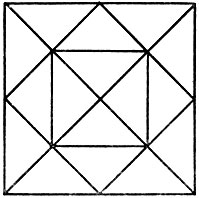
Рис. 22
9.2. Укажите не менее 8 свойств числа 16.
9.3. Какими свойствами обладает биссектриса BD треугольника ABC?
9.4. На прямой отмечены точки А, В, С, D, Е. Сколько отрезков они определяют?
9.5. Укажите основные свойства функции у=|x|-1
9.6. Какими свойствами обладает выражение a+1/a?
9.7. Что вы можете сказать о выражении 3n+1-3n?
9.8. На чертеже (рис. 23) изображен график движения ученика из пункта О в пункт С. Как двигался ученик?
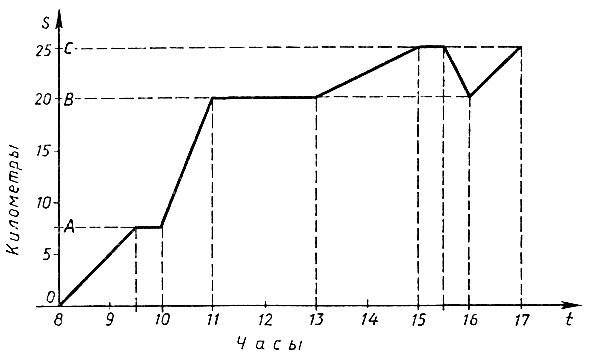
Рис. 23
9.9. На окружности взяты три точки A, B, С, которые затем соединены попарно между собой и каждая соединена с центром окружности. Какие фигуры при этом образовались?
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'