Доклад 3. Как читать математические книги

Учиться нам помогает не только учитель, но и книги, в первую очередь учебники.

Учебники по математике содержат всю информацию о математических знаниях, предусмотренных программой нашего обучения, они помогают в организации нашей учебной работы. Вопросы, задачи, разного рода практические задания, имеющиеся в учебниках, предназначены для того, чтобы в результате их выполнения более глубоко овладеть изучаемыми знаниями, нужными умениями и навыками. Учебники помогают нам в повторении, закреплении, систематизации ранее полученных знаний. Учебники служат и своеобразным справочником, и в случае каких-либо затруднений, в случае, когда мы что-то забыли или нетвердо помним, мы можем взять учебник и в нем найти нужные нам сведения, получить необходимую справку.

Как же устроены учебники по математике?

Каждый учебник разбит на разделы - главы, главы в свою очередь разбиты на параграфы, а те - на пункты. Каждая глава (раздел, тема), параграф, пункт имеют определенное название, которое отражает главное содержание этой главы (параграфа, пункта). Вот, например, первая глава учебника по алгебре для VII класса названа "Рациональные дроби", §1 этой главы - "Преобразование рациональных выражений", а пункт 1 этого параграфа - "Рациональные выражения".

Названия глав, параграфов и пунктов имеются в оглавлении, которое помещается в конце учебника. По этому оглавлению можно узнать, на какой странице начинается та или иная глава, параграф, пункт.

Поэтому, когда нам нужно, например, повторить решение линейных неравенств с одной переменной, то ищем в оглавлении соответствующий пункт. Очевидно, что его надо искать в главе

"Неравенства". В этой главе находим §6 "Неравенства с одной переменной", в этом параграфе находим пункт 17 "Решение линейных неравенств с одной переменной". Напротив него читаем число 68, это значит, что данный пункт начинается с 68-й страницы.

Если же нужно навести справку, например, об определении линейного неравенства с одной переменной, то можно воспользоваться предметным указателем, который имеется в большинстве учебников. Родовым понятием для линейного неравенства является понятие "неравенство", поэтому ищем в предметном указателе, который также помещается в конце книги, но до оглавления, слово "неравенство". Там и находим понятие "неравенство линейное с одной переменной", а рядом число 70, которое означает, что определение этого понятия помещено в учебнике на странице 70.

Заметьте, что ниже имеется такая запись: "- нестрогое 60". Черта, стоящая перед словом "нестрогое", означает, что родовым понятием является вышестоящее слово, т. е. "неравенство". Следовательно, данную запись надо читать так: "Неравенство нестрогое 60", а это означает, что определение нестрогого неравенства имеется на странице 60 учебника.

Примерно так же устроены и справочники по математике.

Кроме учебников и справочников, полезно читать научно-популярную литературу. Много интересного для себя вы найдете в журнале "Квант". Вот еще некоторые книги, которые можно рекомендовать учащимся:

1. Бабинская И. Л. Задачи математических олимпиад.- М., 1975.
2. Балк М. Б., Бал к Г. Д. Математика после уроков.- М., 1971.
3. Белл Э. Т. Творцы математики. Предшественники современной математики.- М., 1979.
4. Болтянский В. Г., Левитас Г. Г. Математика атакует родителей,- М., 1976.
5. Башмаков М. И. Уравнения и неравенства.- М., 1971.
6. Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые.- М., 1970.
7. Гарднер Мартин. Математические головоломки и развлечения.- М., 1971.
8. Гарднер Мартин. Математические новеллы.- М., 1974.
9. Гарднер Мартин. Математические чудеса и тайны.- М., 1978.
10. Гнеденко Б. В. Математика в современном мире.- М., 1980.
11. Гусев В. А., Орлов А. И., Розенталь А. Л. Внеклассная работа по математике в 6-8 классах.- М., 1977.
12. Глейзер Г. И. История математики в школе. IV-VI классы.- М., 1981.
13. Глейзер Г. И. История математики в школе. VII-VIII классы.- М., 1982.
14. Глейзер Г. И. История математики в школе. IX-X классы.- М., 1983.
15. Депман И. Я. Мир чисел.-- Л., 1982.
16. Дышинский Е. А. Игротека математического кружка.- М., 1972.
17. Гуров С. П. и др. П. Л. Чебышев.- М., 1979.
18. Заочные математические олимпиады /Под ред. Н. Б. Васильева и др.- М., 1981.
19. Кордемский Б. А. Увлечь школьников математикой.- М., 1981.
20. Колягин Ю. М., Оганесян В. А. Учись решать задачи.-М. 1980.
21. Дьюдени Генри Э. Кентерберийские головоломки.- М., 1979.
22. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л. Математические соревнования. Арифметика и алгебра.- М., 1970.
23. Лоповок Л. М. Математика на досуге.- М., 1981.
24. Лойд Сэм. Математическая мозаика.- М., 1980.
25. Перельман Я. И. Занимательная алгебра.- М., 1970.
26. Понтрягин Л. С. Метод координат.- М., 1977.
27. Постников. Метод Ферма.- М., 1978.
28. Фаермарк Д. С. Задача пришла с картины.- М., 1974.
29. Фридман Л. М. и др. Как научиться решать задачи.- М., 1979.
30. Эббот Э. Э. Флатландия. Бюргер Д. Сферландия.- М., 1976.

Приступая к чтению книги, надо каждый раз выбирать способ чтения. Ведь можно лишь просматривать нужный материал (раздел, главу), чтобы восстановить в памяти ранее известное. Можно знакомиться с содержанием книги путем внимательного чтения; можно использовать книгу для получения каких-либо справок, условий задач, можно, наконец, не просто читать книгу, а изучать ее. Н. К. Крупская указывала: "Одно из орудий для получения знаний, но орудие очень существенное, это умение пользоваться книгой. И тут надо знать, как надо читать, как выбирать материал, как с ним справиться, как овладеть им".

В каких случаях нам приходится пользоваться учебниками и другими математическими книгами? Вот основные случаи.

1. Нужно найти в учебнике задачи для самостоятельного решения. В этом случае по оглавлению находим, на какой странице начинается указанный параграф или пункт, а затем в нем находим номер указанной задачи. Как правило, условие задачи, если она текстовая, можно не переписывать в тетрадь, а лишь составить краткую запись задачи (модель задачи). Если возникло затруднение в решении, то надо по учебнику внимательно посмотреть предшествующий этой задаче материал, особенно образцы решения задач. Это обычно помогает в поисках решения данной задачи. После решения можно сверить полученный ответ с ответом в учебнике. Ответы помещены в конце учебника.

2. Нужно повторить учебный материал (определение, теорему, вывод формулы и т. д.), изученный на уроке. В этом случае можно поступить по-разному, в зависимости от степени усвоения этого материала на уроке. Если все, что было изучено на уроке, кажется вполне понятным, то тогда, прочитав соответствующее место в учебнике, закрой книгу и попытайся самостоятельно сформулировать определение, записать его, пользуясь математическими знаками, сформулировать и доказать теорему, вывести формулу, т. е. то, что было пройдено на уроке и что только что прочел в учебнике. Если затруднений не встретил и сверка твоих записей с учебником показала, что все правильно, то можно на этом работу закончить.

Если же ты обнаружил, что не можешь правильно воспроизвести содержание прочитанного, то надо не просто прочитать соответствующее место в книге, а изучить его как бы заново.

3. Надо самостоятельно изучить какой-то материал (пункт) по учебнику. Это изучение можно провести по-разному. Можно, читая по частям указанный пункт, одновременно записывать содержание прочитанного в тетрадь, используя математические знаки и символы.

Можно иначе: сначала прочитать весь пункт, не делая никаких записей, затем, если все понятно, закрыть учебник и записать в тетрадь основное содержание математическими знаками и символами. В любом случае надо затем еще раз восстановить устно или письменно содержание изучаемого материала, не заглядывая в книгу. Если, например, задано изучить по учебнику теорему о внешнем угле треугольника, то находим эту теорему в учебнике. Читаем:

"Теорема 4.5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним".

Вспоминаем, что такое "внешний угол треугольника". Про себя повторяем: "Внешний угол треугольника - это угол, смежный с внутренним углом треугольника, при этой вершине".

После этого строим в тетради произвольный треугольник ABC и внешний угол при какой-либо вершине, например - угол CBD (рис. 16). Внутренние углы треугольника, не смежные с этим внешним углом,- будут углы А и С. После этого записываем в тетрадь:

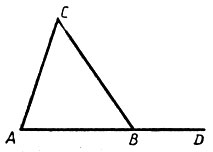
Рис.16

Дано: ΔABC; ∠CBD - внешний Рис. 16 угол ΔABC.

Доказать: ∠CBD=∠A+∠C.

Читаем дальше в учебнике:

Доказательство. Пусть ABC - данный треугольник. По теореме 4.4. ∠A + ∠B + ∠C= 180°. Останавливаемся и вспоминаем теорему 4.4.

Ее формулировка: "Сумма углов треугольника равна 180°".

Читаем дальше: "Отсюда следует, что ∠А+∠В =180°-∠С. В правой части этого равенства стоит градусная мера внешнего угла треугольника при вершине С. Теорема доказана".

Смотрим на свой чертеж и запись теоремы в тетради. У нас взят внешний угол не при вершине С, как в учебнике, а при вершине В. Значит, нам надо будет иначе преобразовывать равенство о сумме углов треугольника. Поэтому пишем в тетради:

Доказательство. По теореме о сумме углов треугольника имеем: ∠А+∠B+∠С=180°. Отсюда: ∠A+∠С= 180°-∠B=∠CBD, что и требуется доказать. После этого, закрыв учебник, по записи в тетради вслух или про себя читаем полностью содержание теоремы и ее доказательство.

Другой пример. Задано изучить по учебнику алгебры пункт "Основное свойство степеней".

В этом случае можно применить второй способ. Читаем весь пункт по учебнику:

31. Основное свойство степеней.

Произведение двух степеней с одинаковыми основаниями всегда можно представить в виде степени с тем же основанием.

Представим, например, произведение х⁸х⁶ в виде степени с основанием х.

По определению степени х⁸ есть произведение восьми множителей, каждый из которых равен х, х⁶ - произведение шести таких же множителей. Следовательно, х⁸х равно произведению 8 + 6 множителей, каждый из которых равен x, т. е. х⁸х=x⁸⁺⁶= х¹⁴.

Вообще если основание степеней а - произвольное число, a m и n - любые натуральные числа, то истинно равенство:

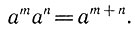
Это равенство выражает основное свойство степени:

Произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей этих степеней.

Можно показать, что это свойство имеет место и в случае, когда число множителей больше двух.

Например, в случае трех множителей имеем:

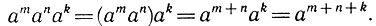
При выполнении преобразований удобно пользоваться правилом: при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Прочитав не спеша, обдумывая каждый абзац, закрываем после этого учебник и записываем в тетради:

Основное свойство степени.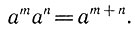

Произведение степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей этих степеней.

Правило. Чтобы перемножить степени с одинаковыми основаниями, надо основание степени оставить прежним, а показатели степеней сложить. a³a⁵a⁴=a³⁺⁵⁺⁴=a¹²

После этого, закрыв тетрадь, вслух или про себя повторяем формулировку основного свойства степени и соответствующее правило. Если при этом что-то забыли, не можем вспомнить, надо еще раз прочитать по своей записи соответствующее место и повторить его еще раз.

4. Нужно по учебнику повторить целый раздел курса. Это приходится делать при подготовке к заключительным урокам по теме или при подготовке к экзаменам. В этом случае следует найти в учебнике нужный материал, прочитать сначала весь материал, ничего не записывая, затем, читая вторично, составить конспект или схему прочитанного.

Конспект представляет собой краткую запись основного, наиболее существенного содержания прочитанного с использованием математических знаков и символов. Схема - это тот же конспект, но расположенный так, чтобы наглядно показать связи и отношения между отдельными частями содержания (понятиями, определениями, теоремами и т. д.). Схема - это сокращенный конспект, из которого отбросили почти весь текстовой материал.

5. Если нужно подготовить доклад, то работа строится следующим образом:

1. подбор нужной литературы;
2. изучение литературы и конспектирование тех разделов, которые непосредственно связаны с темой доклада;
3. отбор наиболее существенного и систематизация всей нужной информации;
4. составление плана доклада;
5. формулирование тезисов доклада в соответствии с планом;
6. подбор иллюстративного материала: чертежей, графиков, примеров, задач и т. д.

Более подробно, как пользоваться книгами, учебниками, можно прочитать в следующих книгах:

1. Николаева Л. А. Учись быть читателем.- М., 1982.
2. Гецов Г. Рациональные приемы работы с книгой.- М., 1975.
3. Поварнин С. Как читать книги.- М., 1978.
4. Попов Г. Техника личной работы.
5. Учись работать с книгой /Сост. Т. К. Крук.

Последний доклад сделал Саша.