Беседа шестая. Понятие случайной величины

Развивающаяся наука не стоит на месте: добавляются новые результаты, появляются новые проблемы, формируются новые понятия, позволяющие глубже и полнее охватить явления природы, а также задачи, возникающие в практической деятельности людей. В теории вероятностей уже в XVIII веке обнаружилось, что одним понятием случайного события и его вероятности обойтись в огромном множестве ситуаций нет возможности. Необходимо иное, более общее понятие, которое было бы способно охватить основные возникшие тогда вопросы. Этим понятием явилось понятие случайной величины, которое возникло не сразу, а продолжало формироваться примерно в течение двухсот лет. Первоначально в XVIII века оно носило чисто интуитивный характер и было связано с задачами, возникавшими в теории ошибок измерений и в демографии. XIX век добавил к ним задачи теории стрельбы, количественных методов в биологии и молекулярной физике. Наконец, наше XX столетие показало необходимость формализации понятия случайной величины на базе современных представлений математики, а также исключительную важность его для научных и непосредственных практических целей.

Представим себе, что мы хотим узнать число зерен пшеницы в колосе и с этой целью срываем несколько колосков. Подсчет показывает, что от колоса к колосу число зерен меняется и нет возможности, взяв тот или иной колос, заранее без подсчета указать число содержащихся в нем зерен.

В молекулярной физике известна следующая задача: молекулы газа движутся в пространстве, их положения и скорости изменяются под влиянием толчков других молекул. Прямолинейный отрезок пути от одного столкновения до следующего носит название свободного пробега молекулы. Спрашивается, как велик свободный пробег? Мы вновь не можем ответить на этот вопрос однозначно, поскольку как моменты столкновений молекулы, которая находится под нашим наблюдением, с другими молекулами, так и скорости молекул, а также направления их движения являются случайными. В результате мы приходим к выводу, что длина свободного пробега молекулы является случайной величиной.

Завод изготовляет конденсаторы. Нас интересует длительность периода безотказной работы каждого из них. Пока еще нет способа, который позволил бы заранее путем вычислений определить эту важную для практики величину. Приходится идти иным путем: ставить некоторую часть продукции на испытания и этим чисто экспериментальным путем определять интересующую нас характеристику. Мы должны сразу же сказать, что если поставим на испытание часть изготовленной партии, скажем двести или триста конденсаторов, то окажется, что все конденсаторы имеют различные сроки безотказной работы. Их жизнь, подобно человеческой жизни, подвержена значительному случайному разбросу. В результате на длительность жизни конденсатора, который мы взяли наудачу из партии, мы должны смотреть как на случайную величину. Значение, которое она примет, не может быть в точности предсказано заранее, оно зависит от случая. Правда, мы должны сказать, что сам этот случай связан со многими обстоятельствами вполне закономерного характера: расположением атомов в веществе, наличием микротрещин и царапин, локальной плотностью материалов и т. д.

Рассмотренные примеры пока дают нам лишь очень общее интуитивное представление о случайных величинах и о важности овладения операциями с ними для целей науки и практики. К сожалению, полученные нами сведения еще не позволяют производить эти операции. По этой причине мы должны будем приступить к более формальному ознакомлению со свойствами случайных величин. Для этой цели мы рассмотрим следующий простой пример.

Представим себе двух игроков в баскетбол. Один из них попадает мячом в сетку в среднем из двух ударов по мячу только раз, другой же из десяти мячей в сетку забрасывает девять. Спросим себя, чему равно число заброшенных мячей при одном бросании первым и вторым игроком? Легко понять, что это число случайно и его возможные значения лишь 0 и 1,- каждый игрок при бросании может попасть, а может и не попасть в сетку. Чем же отличаются две эти случайные величины, раз принимаемые ими значения одинаковы? Очевидно, лишь тем, как часто принимают они каждое из возможных значений. Иными словами, задавая случайную величину, мы должны указать не только ее возможные значения, но и те вероятности, с которыми она их может принимать.

Обозначим через Х₁ число заброшенных мячей при одном ударе для первого игрока и через Х₂ такую же величину, но для второго игрока. В силу условий задачи мы должны написать следующие равенства:

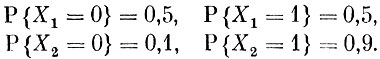
Обратим внимание на то, что изучение случайных событий можно свести к рассмотрению случайных величин. Действительно, пусть нас интересует вопрос о появлении или непоявлении случайного события Е при некотором испытании. Введем в рассмотрение случайную величину X, которая принимает значение 0, если событие F при испытании не наступит, и значение 1, если оно наступило. Очевидно, что мы можем написать такое равенство

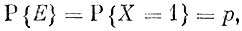
где р означает вероятность появления события Е при испытании.

В теории вероятностей называют совокупность возможных значений случайной величины X и вероятностей, с которыми она их принимает, законом распределения случайной величины X. Мы приведем сейчас несколько примеров законов распределения, которые находят широкое применение в теории и практике.

Распределение Бернулли. Случайная величина μ_η равна числу появлений события Е в n независимых испытаниях, в каждом из которых вероятность наступления события Е одна и та же - р.

Значения, которые может принимать случайная величина μ_η, равны 0, 1, 2, ..., n; их число равно n+1. Вероятность того, что μ_η примет одно из возможных значений, например k, равна

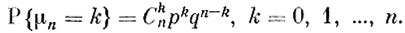
Распределение Бернулли широко используется в теории вероятностей, а также при проведении испытаний.

Гипергеометрическое распределение. Имеются N предметов, М из них белые, а остальные N - М - черные. Наудачу (т. е. с одной и той же вероятностью для каждого из N предметов) вынимаются n предметов. Чему равно число m белых предметов среди выбранных?

Это число случайно, и оно может принимать любое из возможных значений. Найдем теперь, какие же значения может принимать тис какими вероятностями. В зависимости от соотношений, которые имеют место между М, N и n, возможны следующие четыре случая:

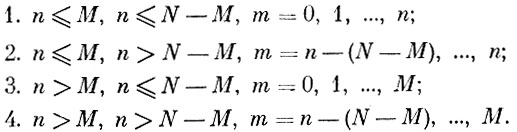
Все эти различные случаи можно объединить в один, если только ввести такие два обозначения: m₀ = max(0, n - (N - М)) и m₁ = min (n, М). Иными словами, m₀ есть наибольшее значение из 0 и n - (N - М), а m₁ - наименьшее из двух чисел n и М. При введении этих обозначений мы можем сказать, что возможными значениями величины m будут все целые числа от m₀ до m₁, т. е.

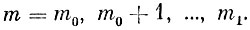
Вероятность, с которой m примет какое-то из возможных значений k, вычисляется легко, она равна

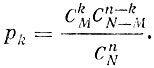
Со случайными величинами, которые распределены гипергеометрически, приходится сталкиваться часто во многих прикладных задачах. Мы упомянем среди этих задач лишь методы статистического приемочного контроля качества массовой продукции.

Заметим, что если все значения случайной величины X исчерпываются следующим набором чисел х₁, х₂, ..., х_n и их вероятности равны соответственно р₁, р₂, ..., р_n, то обязательно должно быть выполнено равенство

Смысл этого равенства состоит в том, что все остальные числа случайная величина X может иметь в качестве своих значений лишь с вероятностью 0.

Распределение Пуассона. В начале прошлого века французский математик С. Пуассон при изучении наблюдений над событиями, имеющими малую вероятность, пришел к рассмотрению распределения, которое в наше время приобрело огромное практическое значение. Возможными значениями для случайной величины X, распределенной по закону Пуассона, являются все целые неотрицательные числа, а вероятности, с которыми она их принимает, задаются формулой

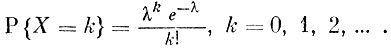
Здесь λ - положительное постоянное, e = 2,7128 ... .

Число возможных значений случайной величины X уже бесконечно.

В последние годы выяснилось с полной определенностью, что распределение Пуассона играет фундаментальную роль в современной физике, в инженерном деле, в вопросах транспорта, связи, в теории надежности и множестве других актуальных направлений. Для примера скажем, что число космических частиц, которое поступает на данную площадку земной поверхности, подчиняется закону Пуассона. Точно так же число морских судов дальнего плавания, которые поступают в данный порт за какой-то определенный промежуток времени, также подчиняется закону Пуассона.

Обратим внимание на то, что все рассмотренные до сих пор примеры случайных величин обладали одной особенностью: множество принимаемых ими значений было конечным или счетным. В реальной же практике встречаются и более сложные случаи, когда возможные значения случайной величины могут быть всеми числами из некоторого промежутка или же просто всеми возможными числами. Для примера, длительность непрерывного горения электрической лампочки может быть любым положительным числом. И мы знаем, что наблюдаются случаи, когда лампочка перегорает в момент включения. В то же время порой лампочки горят в течение тысяч часов без видимого ухудшения качества горения. Точно так же при наблюдении небольшой массы радиоактивного вещества (массы, меньшей критической) промежутки времени между последовательными распадами атомов этого вещества оказываются случайными. Возможные значения этой величины могут быть любыми положительными числами.

Возникает естественный вопрос: как задать вероятности возможных значений случайной величины в только что описанном случае? Само собой разумеется, что указать вероятность каждого из принимаемых значений не представляется возможным. Математика пошла по другому пути и выработала понятие, которое применимо для всех случайных величин и в настоящее время вошло в научную практику. Речь идет о функции распределения случайной величины. Перейдем к рассмотрению этого понятия. Рассмотрим для произвольно выбранного числа х вероятность следующего неравенства: случайная величина X примет значение, меньшее чем х, т. е. символически вероятность неравенства X<х. Очевидно, что вероятность этого неравенства является функцией от х

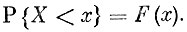
Эта функция и носит название функции распределения случайной величины X.

Знание функции распределения полностью определяет вероятностную природу случайной величины. Мы сейчас выведем простую и важную формулу, крайне необходимую как для теоретических, так и для практических расчетов. Пусть нам нужно найти вероятность попадания значения случайной величины в промежуток от а до b. Рассмотрим три следующих случайных события: событие А - значение X окажется меньшим, чем а (X<а); событие В - значение X окажется меньшим, чем b (X<b); событие С - значение X окажется меньшим, чем b, но не меньшим, чем а (а≤X<b).

Очевидно, что события А и С в сумме составляют событие В и что они несовместимы. Отсюда следует, что

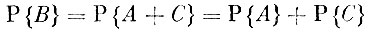
и, следовательно,

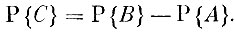
Таким образом,

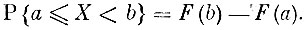
Приведем несколько примеров распределений вероятностей.

Равномерное распределение. Говорят, что случайная величина распределена равномерно в промежутке от а до b, если ее функция распределения имеет следующий вид:

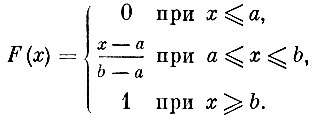
Легко убедиться в том, что если взять несколько промежутков, целиком лежащих в (а, b) и имеющих одну и ту же длину h, то вероятность попадания в них для равномерного распределения одна и та же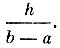

Показательное распределение. Про случайную величину X говорят, что она распределена показательно (экпоненциально), если функция распределения ее имеет такой вид:

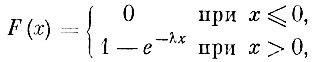
здесь λ - некоторое положительное постоянное.

Показательное распределение впервые встретилось в науке в связи с задачами статистической физики. На рубеже прошлого и настоящего столетий удалось установить, что распределение длины свободного пробега молекулы и длительности свободного пробега (т. е. промежутка времени, в течение которого осуществляется свободный пробег) является показательным. Позднее выяснилось, что это распределение имеет очень широкое значение, поскольку с ним приходится сталкиваться в вопросах надежности сложных систем (распределение промежутка времени между двумя последовательными отказами системы), в задачах ядерной физики, во многих вопросах биологии и организации работы систем связи и транспорта.

Нормальное распределение. Для нормально-распределенной случайной величины X имеет место равенство

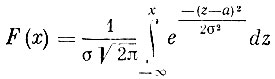
при всех значениях х. Величины а и σ - вещественные постоянные, σ>0.

Впервые с нормальным распределением столкнулся математик Муавр, открывший частный случай одной из важнейших теорем теории вероятностей. В самом начале прошлого века математики обнаружили, что нормальное распределение имеет основное значение для теории ошибок наблюдений. А именно они выяснили, что случайные ошибки измерений подчинены нормальному распределению. При этом α - значение измеряемой величины, а с указывает точность измерений. Позднее была открыта фундаментальная роль нормального распределения для задач биологии, физики, инженерного дела. Особую роль при этом играла так называемая центральная предельная теорема Ляпунова, доказанная на рубеже XIX и XX столетий известным математиком А. М. Ляпуновым, являющимся, кстати сказать, создателем теории устойчивости движения. Теорема Ляпунова, вызывающая до настоящего времени интерес исследователей, в грубых чертах отражает следующий фундаментальный факт: если случайная величина х является суммой почти равноправных независимых между собой случайных величин в очень большом числе и каждая из них большие значения принимает крайне редко, то ее распределение будет близко к нормальному.

Мы только что упомянули ранее не определенное нами понятие независимости случайных величин. Это понятие является одним из центральных во всей теории вероятностей и ее применениях. Именно с ним связаны многие успехи теории и большинства практических применений. Мы скажем, что случайные величины X и Y независимы, если при всех возможных х и y случайные события X<х и Y<y независимы. Иными словами, X и Y независимы, если при любых х и у имеют место равенства

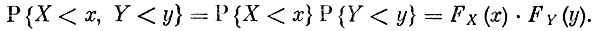
В первых примерах настоящей беседы - распределениях Бернулли, гипергеометрическом, Пуассона - мы также могли бы написать распределения вероятностей. Однако в этих примерах вид функции распределения оказался бы громоздким. Именно поэтому в практическом использовании случайных величин, принимающих лишь дискретный ряд значений, редко пользуются аппаратом функций распределения и предпочитают оперировать с вероятностями принимаемых случайной величиной значений.

Рассмотрим примеры использования понятия функции распределения.

Пример 1. Известно, что распределение группы людей определенной национальности подчиняется нормальному распределению с параметрами а = 172 см и σ = 10 см. Найти вероятность того, что наудачу взятое лицо из этой группы имеет рост, не меньший 190 см; что рост интересующего нас лица окажется между 168 и 173 см.

Для ответа на первый вопрос мы должны воспользоваться формулой для вероятности противоположного события:

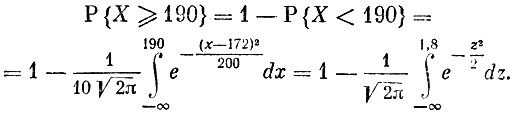
Для вычисления искомой вероятности мы вынуждены использовать специальные таблицы нормального распределения, имеющиеся в каждом учебнике теории вероятностей. Использование этих таблиц приводит нас к равенству

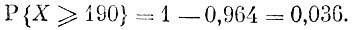
Для ответа на второй вопрос мы используем ранее полученное нами равенство

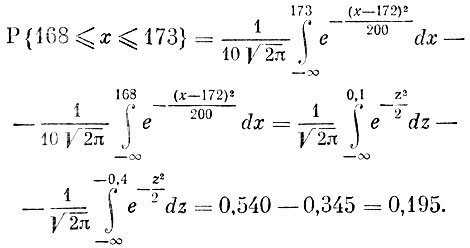
При получении окончательного ответа мы также использовали таблицы нормального распределения.

Согласно полученным нами результатам на каждую тысячу лиц данной группы приходится в среднем 36 человек роста, превосходящего 190 см, и приблизительно 195 человек роста от 168 до 173 см.

Пример 2. Распределение длительности "жизни" сложной системы подчинено показательному распределению с параметром λ = 0,0002. Найти вероятность того, что система проработает безотказно в течение 1000 часов, в течение 3000 часов.

Согласно условию

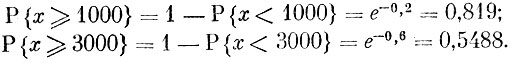
Таким образом, как правило, система безотказно проработает в течение 1000 часов и лишь в половине случаев (немного больше, чем в половине случаев) проработает безотказно в течение 3000 часов. Мы получили общее представление о важном понятии современной науки - случайной величине и ее функции распределения. Дальнейшие факты об этом важном понятии будут даны в следующей беседе.