Беседа седьмая. Закон больших чисел в форме Чебышева

Исчерпывающая характеристика случайной величины задается ее функцией распределения. Зная функцию распределения, мы можем выяснить, какие значения может принимать случайная величина и с какими вероятностями. Однако столь подробное знание не всегда бывает необходимо на практике. Более того, зачастую требуется указать лишь некоторые обобщенные характеристики, чтобы ответить на тот или иной вопрос достаточно определенно. Приведем примеры, которые поясняют последнюю мысль.

Представим себе, что нам необходимо на год сделать запасы некоторого продукта, например зерна, для большой группы лиц. Известно, что потребление хлеба каждым лицом не строго регламентировано, а меняется случайно от одного дня к другому. Едва ли нас устроит при решении этого практического вопроса знание функции распределения. По-видимому, мы станем рассуждать несколько иначе для получения однозначного и при этом удовлетворительного для наших целей ответа. Вот набросок этих рассуждений: поскольку от одного дня к другому потребление данным лицом хлеба меняется, то нам нужно найти среднее потребление данного продукта за день. За длительный срок произойдет взаимная компенсация и суммарное потребление хлеба и окажется равным приблизительно среднедневному потреблению, умноженному на число дней в году. Далее мы умножаем полученное число на численность группы лиц и получаем приблизительный объем необходимых запасов.

В ткацком производстве работница вынуждена время от времени совершать переходы от одного обслуживаемого ею станка к другим, поскольку то на одном из них, то на другом требуется ее вмешательство. Расстояние, которое работница преодолевает, зависит от случая (от какого станка к какому ей придется переходить). Спрашивается, как вычислить среднюю длину перехода? Позднее эту задачу мы решим при двух различных расположениях станков.

Перейдем к определению двух важнейших понятий, вошедших в обиход еще в конце XVII столетия.

Пусть случайная величина х может принимать значения x₁, х₂, ..., х_n соответственно с вероятностями р₁, р₂, ..., р_n.Сумма

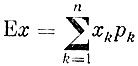
значений случайной величины, умноженных на соответствующие вероятности, называется математическим ожиданием случайной величины х и обозначается символом Ех (в советской и немецкой литературе используется также символ Мх). Нередко вместо термина "математическое ожидание" используют термин "среднее значение случайной величины х".

Пример 1. Мальчик в течение длительного времени завтракал в школе. В зависимости от желаний он покупал в буфете свое любимое блюдо А или другое любимое блюдо В. Первое стоит 30 копеек, а второе - 60. Спрашивается, какую в среднем цену он платил за завтрак, если к концу года оказалось, что в одной трети случаев он заказывал блюдо A и в двух третях случаев - блюдо В.

В нашем примере х₁ = 30, х₂ = 60 и соответственно 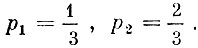По определению средняя цена завтрака равна

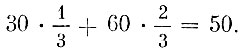
Итак, математическое ожидание стоимости завтрака равно 50 копейкам.

Пример 2. Вероятность появления события А при испытании равна р. Чему равно среднее число появлений события А в одном испытании?

Согласно условию случайная величина μ - число появлений события А в одном испытании - может принимать лишь два значения: 0, если событие А не появится в процессе испытания, и 1, если оно появится. Вероятности этих значений соответственно равны 1 - p и р. Таким образом, среднее значение равно

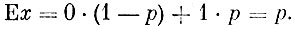
Пример 3. Случайная величина X может принимать все неотрицательные целые значения соответственно с вероятностями

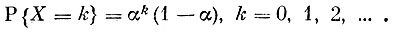
Найти математическое ожидание х.

По определению

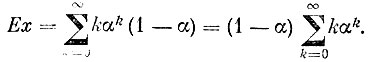
Нам нужно вычислить сумму бесконечного ряда

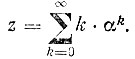
С этой целью представим эту сумму в виде

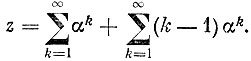
Отсюда путем несложных выкладок получаем

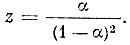
Таким образом,

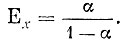
Пример 4. Производится n независимых испытаний, в каждом из которых событие А появляется с вероятностью р. Чему равно математическое ожидание числа появлений события А в этих испытаниях?

Обозначим через μ число появлений события А в n испытаниях. Мы знаем из предыдущей беседы, что μ может принимать любые из следующих значений 0, 1, 2, ..., n, и только эти значения. Вероятности каждого из возможных значений вычисляются по формуле Бернулли

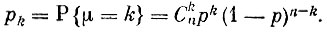
Математическое ожидание величины μ, таким образом, равно

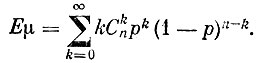
Эта сумма была нами вычислена при доказательстве закона больших чисел в формуле Бернулли. Окончательно оказывается

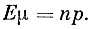
Немного позднее мы увидим, что можно избежать вычислений встретившейся суммы, если воспользоваться теоремой о математических ожиданиях.

Пример 5. Рабочий обслуживает n однотипных станков, расположенных на прямой линии так, что между соседними станками расстояние равно а. Необходимость вмешательства рабочего на станках возникает в случайные моменты времени, независимо друг от друга. Найти математическое ожидание длины перехода между станками (рис. 3).

Рис. 3

Пронумеруем станки слева направо от 1-го до n-го и обозначим через В_k событие, состоящее в том, что рабочий находится у станка с номером к. Так как все станки по условию задачи однотипные, то вероятность того, что рабочему придется переходить от k-то станка к i-му, одинакова для всех значений i, т. е. равна 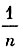. Величина перехода при этом равна

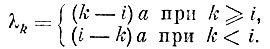
По определению

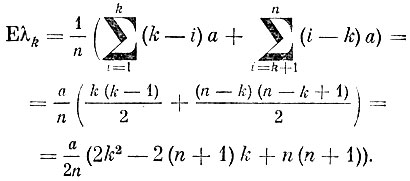
Вероятность того, что рабочий находится у k-то станка, равна 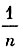, поэтому математическое ожидание перехода равно

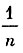
Известно, что

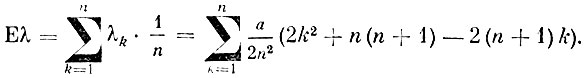
поэтому

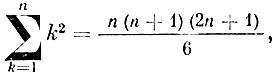
где l = (n - 1)а означает расстояние между крайними станками.

Мы ограничиваемся рассмотрением только то,го случая, когда случайная величина может принимать конечное или счетное множество значений. Все остальные, более сложные случаи, требуют значительных познаний в области математики, и мы их не рассматриваем здесь. Этим обстоятельством вызвано и то, что последующие теоремы мы докажем при этом дополнительном ограничении.

Теорема 1. Математическое ожидание постоянного равно этому постоянному: Еc = с.

Доказательство теоремы таково: на постоянную мы можем смотреть, как на случайную величину, принимающую единственное значение с вероятностью 1. Отсюда немедленно вытекает утверждение теоремы.

Теорема 2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

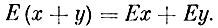
Действительно, пусть х принимает значения х₁, х₂, ..., х_n соответственно с вероятностями p₁, p₂, ..., p_n, а y - значения y₁, y₂, ..., y_m с вероятностями q₁, q₂, ..., q_m. Обозначим через р_ij вероятность того, что х примет значение x_i, а y - значение y_j

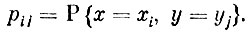
Все возможные значения х + y, очевидно, равны x_i + y_i, а потому

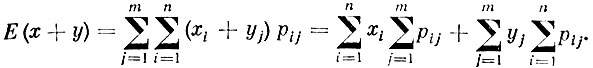
Но по формуле полной вероятности

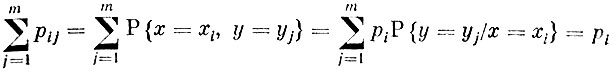
и

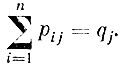
Таким образом,

Нам важно отметить, что доказанная теорема верна всегда - и когда слагаемые х и y независимы и когда они как угодно зависимы. Это обстоятельство очень существенно как в теоретическом, так и в прикладном отношениях.

Нет нужды доказывать, что теорема 2 распространяется на любое конечное число слагаемых. Проиллюстрируем применение доказанной теоремы примерами.

Пример 6. Рассмотрим пример 4 настоящей беседы на базе теоремы 2.

Число появлений μ события А в n независимых испытаниях можно представить в виде следующей суммы

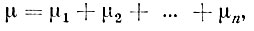
где μ_i - число появлений события А в i-ом испытании. Из примера 2 настоящей беседы мы знаем, что Еμ_i = р при любом i. Применение к только что написанной сумме теоремы 2 приводит нас к равенству

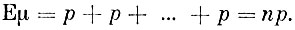
Пример 7. По некоторой цели стрельба ведется до n-го попадания. Считая, что выстрелы производятся независимо друг от друга и вероятность попадания при каждом выстреле равна р, найти математическое ожидание числа необходимых для выполнения задачи снарядов.

Обозначим через v_k число снарядов, потраченных от (k-1)-го до k-то попадания. Очевидно, что расход снарядов на n попаданий равен

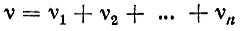
и, следовательно,

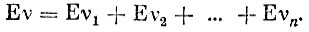
Но

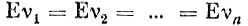
и

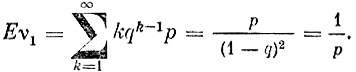
Таким образом,

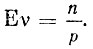
Доказанных теорем нам недостаточно, поскольку очень важно иметь общие законы образования математического ожидания произведения случайных величин по известному математическому ожиданию сомножителей. В общем случае таких законов нет, но для важнейшего частного случая мы сейчас его получим.

Теорема 3. Математическое ожидание произведения двух независимых случайных величин х и y равно произведению математических ожиданий сомножителей

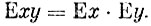
Для независимых случайных величин х и y вероятность того, что сразу будут выполнены два равенства

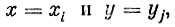
равна произведению вероятностей каждого из этих равенств:

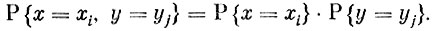
Теперь очевидно, что мы можем написать следующую цепочку равенств

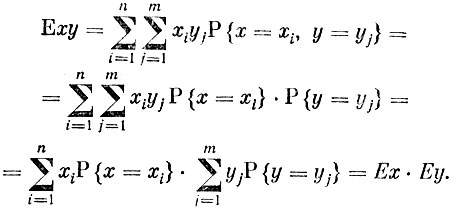
Пример 8. По проводнику, сопротивление которого зависит от ряда случайных причин (изменение температурных условий, влажности окружающей среды и т. д.), течет электрический ток, сила которого также зависит от случая. Известно, что среднее значение сопротивления проводника R = 25 Ом, а средняя сила тока I = 6 А. Известно, что сила тока и сопротивление проводника независимы. Найти среднее значение электродвижущей силы ε.

По закону Ома известно, что

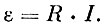
Согласно теореме 3 и условиям задачи из этой формулы находим, что

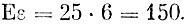
Мы укажем одно простое и важное следствие из теоремы 3.

Следствие. Постоянный множитель можно выносить за знак математического ожидания:

Для характеристики случайных величин, помимо математического ожидания, широко используется другая числовая характеристика. Ее значение мы выясним еще в настоящей беседе. Сейчас же попытаемся понять ее назначение. Представим себе, что мы производим измерения некоторой величины и можем при этом совершать абсолютно точный замер, а также совершать ошибки, сочтя измеряемую величину равной не ее истинному значению а, а величинам или а-α или a+α. Вероятность точного замера равна 1 - р, а каждое ошибочное измерение производится с вероятностью ^р/₂. Легко подсчитать, что каковы бы ни были р и α математическое ожидание результата измерения будет равно измеряемой величине. Однако о точности измерений у нас будут различные суждения в зависимости от значений р и ε. Если р велико так же, как и ε, то мы сочтем измерения неудачными, обладающими большим разбросом. В то же время, если р мало или же мало ε, то мы будем склонны считать измерения успешными, дающими хорошую точность и обладающими малым разбросом. Представление о разбросе значений случайной величины почти всегда играет большую роль, а не только в рассмотренном качественном примере.

В теории вероятностей для измерения разброса значений случайной величины используют понятие дисперсии, т. е. математическое ожидание квадрата отклонения случайной величины X от ее математического ожидания:

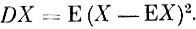
Из определения ясно, что дисперсия является неотрицательной величиной и обращается в нуль, только если случайная величина X обращается в постоянную.

Дисперсии можно придать другую форму. Поскольку

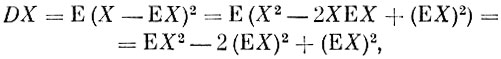
то

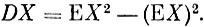
В зависимости от обстоятельств для вычислений дисперсии лучше пользоваться или первой или второй из приведенных формул.

Поскольку дисперсия любой случайной величины неотрицательна, из второй формулы мы делаем такой важный вывод: математическое ожидание квадрата случайной величины не меньше квадрата ее математического ожидания.

Пример 9. Найти дисперсию числа появлений события А в одном испытании, если вероятность события А равна р.

Рассмотрим случайную величину μ, равную числу появлений события А при испытании. Мы знаем из предыдущего, что эта величина принимает лишь значения О и 1 соответственно с вероятностями 1 - р и р. Те же значения и с теми же вероятностями принимает и величина μ². Таким образом,

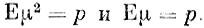
Согласно второй из приведенных формул для дисперсии находим

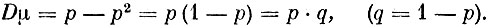
Приведем две теоремы относительно дисперсий.

Теорема 4. Постоянный множитель выходит за знак дисперсии в квадрате:

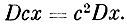
Теорема является непосредственным следствием из теорем о математических ожиданиях.

Теорема 5. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий

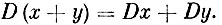
Действительно,

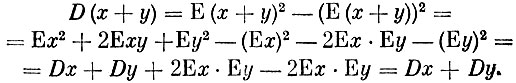
Доказанная теорема очевидным путем обобщается на сумму произвольного конечного числа слагаемых.

Пример 10. Найти дисперсию числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события А равна р.

Как и в примере 6, представим число появлений события А в n испытаниях в виде суммы 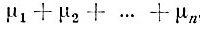. Для каждого слагаемого дисперсия уже найдена в примере 9. Искомая величина равна, таким образом,

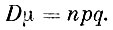
Мы возвратимся теперь к идеям, которые были изложены нами в связи с законом больших чисел в форме Бернулли. В первой половине XIX столетия в связи с задачами теории стрельбы Пуассон обобщил теорему Бернулли на случай испытаний, в которых вероятность появления события А меняется вместе с номером испытания. Очень широкое обобщение, включившее в себя в качестве простейших частных случаев как теорему Бернулли, так и теорему Пуассона, было получено в начале шестидесятых годов прошлого века одним из крупнейших математиков того времени П. Л. Чебышевым. Теорема Чебышева интересна не только широтой формулировки, но и исключительно простой идеей доказательства. В основе его рассуждений лежит неравенство, доказанное Чебышевым и впоследствии нашедшее многочисленные применения как в теории вероятностей, так и в других математических дисциплинах - теории чисел, теории функций, теории динамических систем и др.

Лемма Чебышева. Если случайная величина х имеет конечную дисперсию, то при любом положительном а имеет место неравенство

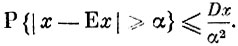
Пусть х_i - возможные значения х и p_i - их вероятности, тогда согласно определению

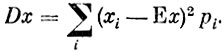
Если в этой сумме отбросить все слагаемые, для которых |x_i - Ех|≤α, и сохранить лишь те, для которых |x_i - Еx|>α то от этого сумма может только уменьшиться. Таким образом,

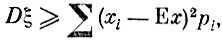
где сумма распространяется лишь па те значения i, для которых

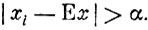
Сумму, стоящую справа, мы уменьшим еще больше, если все множители (x_i - Ex)² заменить на допустимое минимальное значение α². В результате

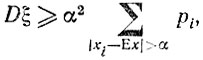
но, поскольку

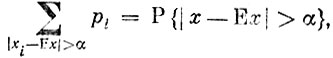
лемма доказана полностью.

Теперь мы можем перейти к выводу закона больших чисел в форме Чебышева.

Теорема Чебышева. Если независимые случайные величины x₁, x₂, ..., х_n, ... имеют математические ожидания Ex_n = a_n и дисперсии, ограниченные одним и тем же числом С, то при любом α>0 и n→∞

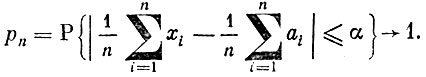
Для доказательства заметим, что события

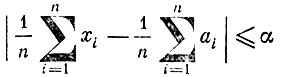
и

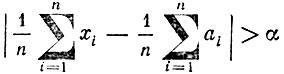
противоположны и, следовательно,

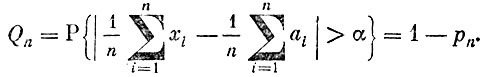
Согласно неравенству Чебышева

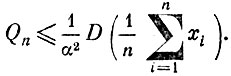
Но в силу теорем 4 и 5

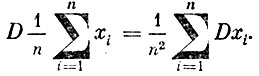
А так как согласно условию Dx_i≤C, то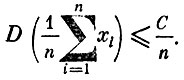

Теперь очевидно, что при n→∞

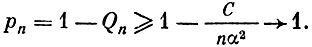
Теорема доказана.

Мы укажем теперь два частных случая доказанной теоремы.

Случай 1. Если x_i может принимать только два значения - 1 с вероятностью р и 0 - с вероятностью q = 1 - p, то теорема Чебышева автоматически превращается в теорему Бернулли.

Случай 2. Пусть условия теоремы Чебышева выполнены и, кроме того Ex_i = а при всех i, тогда при любом α и n→∞

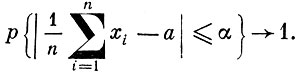
Этой теореме можно придать такую интерпретацию: предположим, что n наблюдателей измеряют величину a без систематической ошибки и допускаемая ими точность сравнима по величине (нет наблюдателей, которые систематически допускают очень большие ошибки). В этих условиях среднее арифметическое результатов их измерений (при большом числе наблюдателей) с вероятностью, близкой к единице, будет мало отличаться от измеряемой величины. В этом следствии можно видеть основание принципа среднего арифметического, который так широко используется в экспериментальных науках.

Теорема Чебышева вскрывает глубокие закономерности мира случайных явлений. Оказывается, что при некоторых довольно общих условиях совместное действие большого числа независимых ингредиентов оказывается с большой вероятностью практически постоянным. В этом лежит обоснование многих законов физики, экономики и других областей знания, в которых приходится иметь дело с воздействием большого числа причин.

Теория вероятностей - наука о случайных явлениях - находится в состоянии интенсивного развития. Она тесно связана с развитием естествознания и разнообразных направлений практической деятельности. Это вызвано тем, что она позволяет достаточно полно отразить ту сложность ситуаций, с которыми приходится сталкиваться в реальных условиях. Теория вероятностей является сильнейшим орудием познания, которое широко используется теперь, но получит еще большее значение в будущем.