Упражнения

1. В урне 9 белых и 1 черный шар. Сколько раз нужно произвести извлечения шаров из урны (с возвращением вынутого шара в урну), чтобы извлечь черный шар по меньшей мере один раз с вероятностью, не меньшей 0,9?
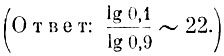
2. Два шахматиста условились сыграть 10 партий. Вероятность выигрыша каждой партии первым игроком равна ²/₃, вероятность проигрыша партии вторым игроком равна ¹/₃ (ничьи не принимаются во внимание). Чему равна вероятность выигрыша всей игры первым игроком, вторым игроком, вероятность ничьей? Под выигрышем всей игры понимается выигрыш более половины всех сыгранных партий. (Ответ: 0,7869; 0,0765; 0,1366.)