Беседа пятая. Схема Бернулли

Мы познакомимся теперь с одной очень простой, но очень важной для теории и применений математической моделью, получившей в литературе наименование схемы независимых испытаний или схемы Бернулли. Последнее название было дано в честь выдающегося швейцарского математика Якова Бернулли, подробно изучившего эту схему и получившего ряд результатов, сохранивших свое научное значение до нашего времени. Значение схемы Бернулли выходит далеко за пределы ее непосредственного применения к разнообразным практическим задачам. За последние четверть тысячелетняя достаточно определенно выяснилось, что закономерности, выведенные первоначально лишь для этой схемы, обладают способностью к обобщению на более сложные случаи. Впоследствии мы убедимся в этом на примере закона больших чисел.

Представим себе, что производится последовательность испытаний, в каждом из которых может произойти некоторое событие А с одной и той же вероятностью в каждом из испытаний. При этом мы предположим, что вероятность события А, которую станем обозначать буквой р, не изменяется от того, что нам становятся известными результаты предыдущих или же прогноз последующих испытаний. Это и называется независимыми испытаниями.

Основной вопрос, который здесь возникает, состоит в следующем: произведены n независимых испытаний. Спрашивается, чему равна вероятность того, что в каких-то m (0≤m≤n) из них наступит событие А? Ответ на этот вопрос дают так называемые формулы Бернулли, к выводу которых мы и перейдем после рассмотрения нескольких примеров, которые позволят нам составить общее представление о широте и разнообразии задач, приводящих к схеме Бернулли.

Пример 1. На испытательный стенд поставлены 20 ламп накаливания и испытываются под нагрузкой в течение 1000 часов. Вероятность того, что лампа выдержит испытание, равна 0,8 и не зависит от того, что случилось с другими лампами.

Чему равна вероятность того, что за время испытаний откажут 0 ламп, 2 лампы, 4 лампы?

В данном примере под испытанием понимается проверка лампы на ее способность выдержать нагрузку в течение 1000 часов, число испытаний, таким образом, равно n = 20, событие А состоит в отказе лампы (она не выдержит испытания), р = Р {А} = 0,2. Нас интересуют три значения m - 0, 2 и 4.

Пример 2. В семье 10 детей. Вероятность рождения мальчика и вероятность рождения девочки одинаковы и равны 0,5. Кроме того, вероятность рождения мальчика (и девочки) не зависит от того, какие дети рождались в семье раньше. Чему равна вероятность того, что в семье 5 мальчиков и 5 девочек, все 10 - девочки, не больше 5 мальчиков?

В этом примере под испытанием понимается рождение ребенка, р = 0,5, n = 10.

Пример 3. Вероятность того, что в колосе пшеницы некоторого сорта окажется более 120 зерен, равна ¹/₃. Взяты шесть колосьев. Чему равна вероятность того, что более 120 зерен окажется в 0, 1, 2, 3, 4, 5, 6 из них?

Ясно, что здесь n = 6, р = ¹/₃ и m пробегает все возможные значения от 0 до 6.

Приступим теперь к выводу формул Бернулли.

Найдем вероятность того, что в испытаниях с определенными номерами (например, с номерами 1, 2, ..., m или 2, 3,..., m+1) событие А произойдет, а в остальных не наступит (т. е. наступит событие А). Но такой выбор номеров испытаний может быть произведен различными способами. Число таких способов, очевидно, равно числу сочетаний из n элементов по m. Но в силу теоремы умножения вероятностей вероятность того, что событие А наступит при определенных m испытаниях и при остальных n - m оно не наступит, равна р^m(1 - р)^n-m. Для каждого такого выбора эта вероятность одна и та же. Таким образом, по теореме сложения вероятностей искомая вероятность равна

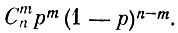
Найденную вероятность обычно обозначают символом Р_n (m) и вероятность ненаступления события А (т. е. наступления события 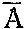) - буквой q (q = 1 - р). Таким образом,

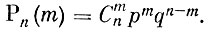(1)

Полученная формула и является формулой Бернулли; в ней аргумент m может принимать значения 0, 1, 2, ..., n.

Теперь мы имеем возможность довести до конца приведенные ранее примеры.

Пример 1. Согласно условию задачи нам нужно найти вероятности Р_n (0), Р_n (2) и Р_n (4), при этом n = 20, Р = 0,2.

Использование формулы (1) приводит нас к равенствам:

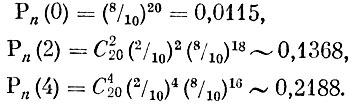
Пример 2. В данном примере вероятность рождения девочки (событие А) равна ¹/₂. Таким образом,

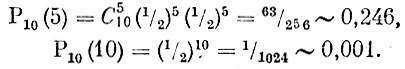
Нам осталось ответить на третий вопрос: чему равна вероятность того, что в семье не больше 5 мальчиков? Это означает, что в семье или 5 мальчиков, или 4, или 3, или 2, или 1, или, наконец, все дети в семье - девочки. Все перечисленные события несовместимы, и потому искомая вероятность по теореме сложения равна

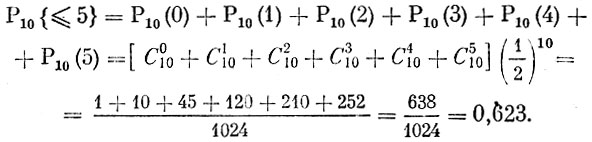
Пример 3. В рассматриваемом примере n = 6, 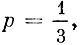и нам нужно найти вероятности всех возможных исходов испытаний. Согласно формуле Бернулли

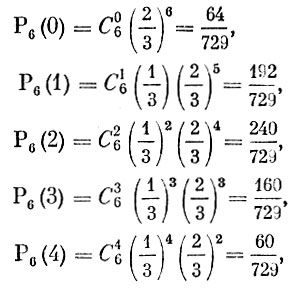
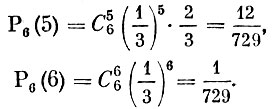
Заметим, что появление события А в n независимых испытаниях 0, 1, 2, ..., n раз являются несовместимыми событиями и единственно возможными. Менее 0 раз событие А появиться не может, также как более чем n раз ему наступить невозможно. Таким образом, в сумме перечисленные события образуют достоверное событие и, следовательно, выполняется равенство

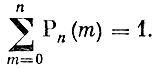(2)

Но при каждом испытании может произойти либо событие А, либо событие . Таким образом, для каждого испытания выполняется равенство

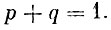
В n испытаниях в силу теоремы умножения вероятностей

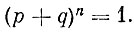
Из сравнения левых частей двух только что написанных равенств мы заключаем, что

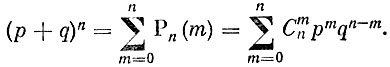
Отсюда, положив

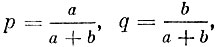
где а и b - произвольные неотрицательные числа, находим

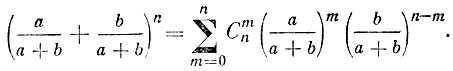
После умножения обеих частей этого равенства на (a+b)ⁿ получаем

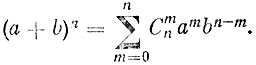(3)

Это равенство является частным случаем широко известной формулы бинома Ньютона (эта формула верна для любых значений а и b, в том числе и для чисел, принимающих значения разных знаков). Формула бинома Ньютона была известна математикам Средней Азии за несколько сот лет до рождения Ньютона, но оставалась неизвестной математикам Европы.

Изучим теперь вероятность Р (m) как функцию аргумента m, который может принимать лишь целочисленные значения от 0 до n. Результаты примера 3 наводят на мысль, что следует ожидать такого поведения Р_n (m): при возрастании m функция Р_n (m) сначала возрастает, затем достигает максимального значения и после этого начинает убывать. Докажем, что это предложение правильно. Для этого рассмотрим отношение

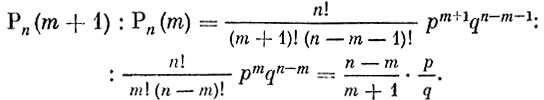
Вероятность Р_n (m + 1) будет больше, равна или меньше вероятности Р_n (m) в зависимости от того, будет ли отношение 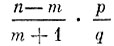больше, равно или меньше 1. В частности, Р_n (m + 1) окажется большей Р_n (m), т. е. возрастает в точке m, если

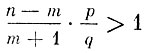
или иначе, если

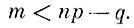
Таким образом, Р_n (m) возрастает при увеличении m от 0 до np-q. Если

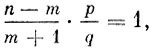
т. е. если m = np - q (это равенство возможно лишь в редких случаях, когда разность np - q является неотрицательным целым числом), то

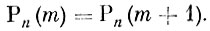
Наконец, Р_n (m + 1) <Р_n (m), если

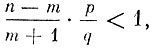
т. е. если m> np - q.

Поведение функции Р_n (m) теперь выяснено полностью: она возрастает, пока m остается меньшим величины np - q, достигает максимума и для m, больших np - q, убывает. В том случае, когда np - q является целым числом, функция Р_n (m) достигает максимального значения в двух точках, а именно при m = np - q и m + 1 = np + q. При этом

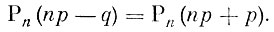
Пример 4. Вероятность события А равна ³/₅, n = 19. Какое число появлений события А имеет максимальную вероятность?

Поскольку

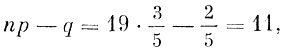
максимальная вероятность достигается при двух значениях m, а именно при m = 11 и m = 12. Эта вероятность равна

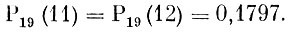
Только что обнаруженный характер поведения вероятностей Р_n (m) при изменении m может быть значительно уточнен. Оказывается, что вблизи от точки np - q не только находится максимальное значение вероятности Р_n (m), но в сумме ближайшие значения Р_n (m) оказываются очень близки к 1. Иными словами, вероятность того, что m примет сравнительно малое или сравнительно большое значение, оказывается близкой к нулю.

Обозначим через и, число появлений события А в n независимых испытаниях. Это число зависит от случая и может принять любое целое значение от 0 до n. Рассмотрим разность 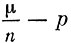и докажем, что чем больше и, тем реже она может значительно уклоняться от нуля. Более того, какое бы малое число ε>0 мы ни взяли, например 0,0001 или 0,0000001, по абсолютной величине разность 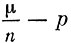с вероятностью, как угодно близкой к единице, окажется меньшей, чем ε. Точнее, в виде формулы это утверждение можно записать таким образом: каковы бы ни были ε>0 и η>0, при достаточно большом n имеет место неравенство

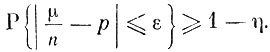
Отношение 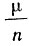носит название частоты события А. Теорема Бернулли, таким образом, утверждает, что при больших значениях n частота события А оказывается близкой к его вероятности. Это обстоятельство широко используется для приближенной оценки неизвестных вероятностей, для проверки гипотез относительно значений вероятностей интересующих нас событий. Именно этим путем на основании длительных и тщательных наблюдений была оценена вероятность рождения ребенка определенного пола, оценивается качество изготовления продукции.

Мы приступим теперь к доказательству теоремы Бернулли. Это потребует от нас довольно значительных вычислений, которых можно избежать, если воспользоваться одним неравенством П. Л. Чебышева, с которым мы познакомимся в одной из следующих бесед.

Вычислим предварительно следующие суммы:

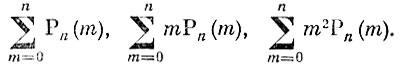
Значение первой из них было нами уже показано. Оказалось, что

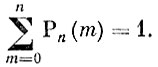(5)

Теперь

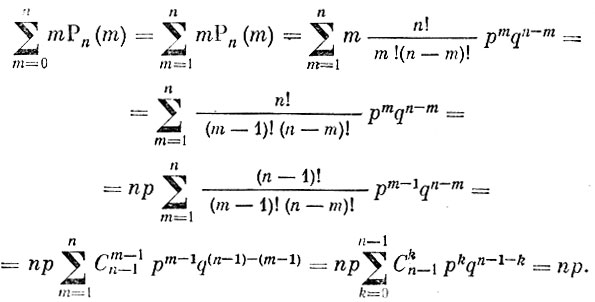
Последнее равенство написано на основании тождества (2) для значения n, равного n-1. Итак,

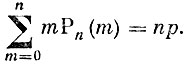(6)

Теперь

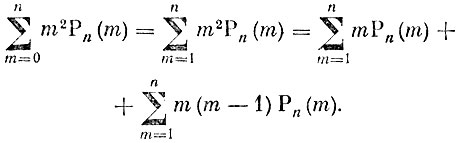
Первое слагаемое этой суммы нам уже известно, оно равно np, поэтому

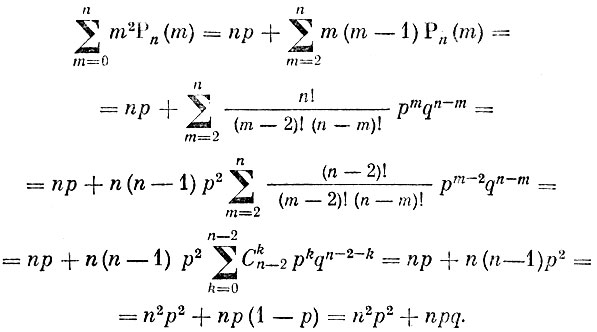
Здесь равенство

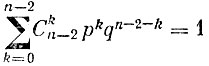
написано на основании (2), в котором n заменено на n-2. Итак,

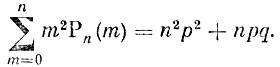
Заметим, что случайные события

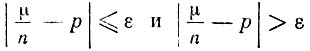(7)

противоположны, а потому

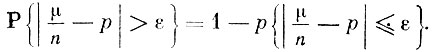
В силу теоремы сложения вероятностей

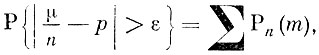
где сумма распространена па те значения m, для которых 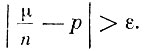Но для этих значений

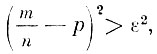
и поэтому

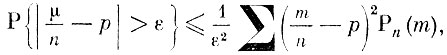
где сумма по-прежнему распространена на те значения m, для которых 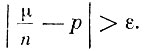Очевидно, что эта сумма может только возрасти оттого, что суммирование будет распространено на все возможные значения n. Таким образом,

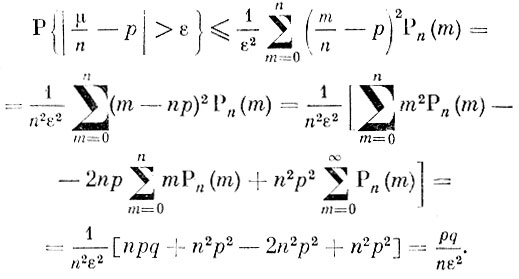
На последнем этапе вычислений мы воспользовались равенствами (5) - (7). Теперь ясно, что

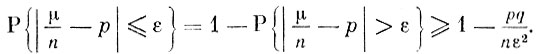(8)

Но отсюда вытекает, что при любом положительном ε вероятность 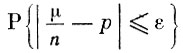может быть сделана сколь угодно близкой к 1, если только выбрать n достаточно большим. Теорема Бернулли доказана.

Неравенство (8) необходимо не только для проведенного доказательства, но и для оценки некоторых вероятностей. Проиллюстрируем это утверждение на простом примере.

Пример 5. В некотором городе ежегодно рождается 10 000 детей, вероятности рождения мальчика и девочки равны 0,5. Чему равна вероятность того, что число родившихся мальчиков отклонится от 5000 не более чем на 1 % от общего числа родившихся в течение года в этом городе?

Искомая вероятность равна

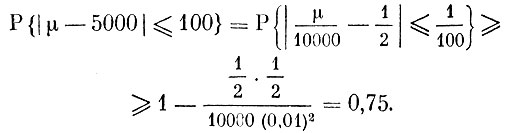
Для оценки вероятности мы воспользовались неравенством (8).

Пример 6. Вероятность события А в каждом из независимых испытаний равна 0,8. Спрашивается, сколько испытаний достаточно произвести, чтобы с вероятностью 0,9 быть уверенным в том, что частота события А уклонится от вероятности р = 0,8 не более чем на 0,5?

Нам нужно найти такое n, для которого

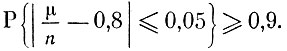
Согласно (8) для этого достаточно n выбрать так, чтобы выполнялось равенство

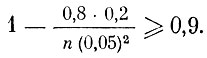
Отсюда n = 640. Стольких испытаний достаточно для стоящих перед нами целей. В действительности полученная оценка может быть понижена, но это требует значительно более сложных математических средств.

Заметим, что вся теория, которая была развита в настоящей беседе, нигде не опирается на данное нами ранее классическое определение вероятности. Вероятность р может быть не только рациональной дробью, но и любым неотрицательным числом, меньшим или равным 1.

Охра цвет, выставка в олимпийском стендовый моделизм.