Беседа четвертая. Элементы комбинаторики

Для подсчета числа равновероятных случаев теория вероятностей широко использует методы и результаты ветви математики, получившей название комбинаторики, последние годы интерес к комбинаторике резко возрос не только в связи с теорией вероятностей, но и со многими другими направлениями математической мысли. Здесь будут изложены лишь первичные элементы комбинаторики, которые нам пригодятся немедленно как для решения задач, так и для доказательства важных формул, носящих имя автора - швейцарского математика конца ХVII - начала XVIII века Якова Бернулли.

Представим себе, что имеются n каких-то предметов (не обязательно имеющих материальную природу), отличающихся друг от друга какими-то признаками, например номерами, названиями, индексами и т. д. Пусть, для примера, это будут книги А₁, А₂, ..., А₂₀ (здесь n = 20).

Размещением из n предметов по к называется группа каких-то к предметов из этих n, расположенных в определенном порядке. Различными считаются размещения, в которых имеются или различные элементы, или если все элементы одинаковы, но различны порядки их расположения.

В примере с книгами мы приведем несколько размещений: А₅, А₇, А₁₁; А₇, А₁₁, А₅; А₁₁, А₅, А₇; А₂, A₄, A₆ и т. д. Первые три размещения из 20 элементов по 3 отличаются только порядком элементов, четвертое имеет другие элементы.

Часто возникает необходимость подсчета числа возможных размещений. Это число обычно обозначается символом А^k_n. Непосредственный подсчет числа А^k_n обычно затруднителен, поскольку даже для сравнительно малых значений n и k это число принимает очень большие значения. Так, в нашем примере, как мы вскоре сумеем это проверить, оказывается, что А³₂₀ = 6840.

Для вывода общей формулы мы поступим следующим способом: разобьем все размещения на n не пересекающихся между собой групп. В первую группу отнесем все размещения, которые начинаются с первого предмета, во вторую - начинающиеся со второго, и т. д. Теперь, поскольку в каждой группе первый предмет фиксирован, каждую группу мы можем разбить на n-1 подгруппу: в первую подгруппу первой группы мы отнесем все размещения, которые на втором месте имеют второй предмет, во вторую подгруппу - все размещения, у которых на втором месте стоит третий предмет, и т. д. В результате мы получим n(n-1) различных подгрупп. Эту операцию мы станем продолжать дальше, пока не подойдем к фиксации предмета на k-ом месте. Такой элемент по необходимости можно выбрать лишь n - (k-1) способами (k-1 элемент был уже закреплен). Таким образом, число групп при первом подразделении оказалось n, при втором n(n-1), при третьем n(n-1)(n-2). Общее же число групп при окончательном разбиении оказывается равным (n(n-1), .,.,(n-k+1). Одновременно это число оказывается равным и числу всех размещений (поскольку при последнем разбиении мы фиксируем и последний элемент). Итак, окончательно мы находим, что

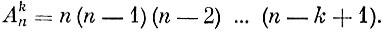(6)

Перестановками называются размещения из n предметов по n. Число всех перестановок согласно формуле (6) равно

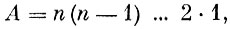(7)

т, е. произведению всех целых положительных чисел от 1 до n. Это произведение обозначается символом n! и произносится n факториал. Очевидно, что при n≥2 факториал обладает следующим свойством

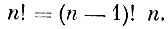
Чтобы это равенство имело смысл при всех целых положительных значениях n, по определению положим 0! = 1.

Формулу для A^k_n теперь мы можем записать в несколько ином виде

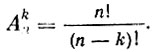(8)

Сочетанием из n различных предметов по к называется произвольная группа к предметов из этих n. Различными называются сочетания, различающиеся между собой хотя бы одним элементом. Найдем теперь формулу для числа всех возможных сочетаний из n предметов по k. Это число обозначается символом С^k_n, а также (^k_n).

Обратим внимание на то, что если мы наряду с каждым сочетанием станем рассматривать и все перестановки из составляющих его элементов, то мы получим всевозможные размещения. Таким образом, выполняется равенство

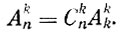
Отсюда

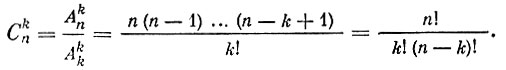(9)

По определению положим

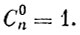
Из формулы (9) немедленно вытекает полезное равенство

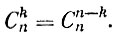
Пример 7. В группе М + N предметов М предметов обладают некоторым свойством В, а остальные N предметов этим свойством не обладают. Из этих предметов наудачу вынимаются к предметов. Спрашивается, чему равна вероятность того, что среди вынутых окажутся m предметов со свойством В и n = k - m предметов, не обладающих этим свойством?

Под исходом здесь следует понимать появление любых к предметов из М + N. Поскольку нас не интересует порядок появления предметов, то общее число различных исходов равно 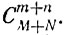Очевидно, что в задаче следует считать 0≤m≤М и 0≤n≤N, поскольку если эти условия не выполнены, то вероятность интересующего нас события должна быть равна нулю. Извлечь m предметов со свойством В можно С^m_N различными способами. Точно так же n из N можно извлечь Cⁿ_N различными путями. Поскольку для любого выбора m предметов со свойством В можно извлечь n предметов, не обладающих этим свойством Сⁿ_N способами, то искомая вероятность равна

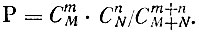
Рассмотренная задача имеет многочисленные применения, в частности в вопросах контроля качества массовой продукции.

Пример 8. Вместе живут n друзей. По утрам к завтраку один из них должен отправляться за покупками. Чтобы выбрать ответственного за покупки, друзья тянут жребий: на одной из бумажек поставлен знак +; лицо, вытянувшее эту бумажку, и обязано делать покупки. Для кого вероятность вытянуть "печальный" жребий минимальна: для того, кто тянет первым, вторым, ..., последним?

Найдем вероятность, что билет со знаком "+" достанется тому, кто тянет билет k-ым по очереди. Всего исходов может быть n!, поскольку билеты могут появиться в любом порядке. Благоприятствующие интересующему нас событию будут все исходы, в которых билет "+" зафиксирован на k-ом месте, а остальные n-1 билетов располагаются в произвольном порядке. Таких исходов может быть (n-1)!. Таким образом, вероятность p_k, что билет достанется тому, кто вытягивает k-ым по очереди, равна

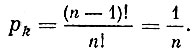
Для всех к эта вероятность одна и та же, так что, каким бы по очереди не вытягивать жребий, вероятность вытянуть один единственный "+" остается неизменной.