Беседа третья. Условная вероятность

В предыдущей беседе мы узнали, что для вычисления вероятности суммы двух событий А и В, вообще говоря, недостаточно знать только вероятности каждого из этих событий в отдельности. Если эти события совместны, то нам нужно дополнительно знать также вероятность события АВ, т. е. вероятность совместного осуществления событий А я В: Ближайшая паша задача как раз и будет заключаться в том, чтобы установить способ вычисления вероятности произведения событий. Ее решение потребует от нас введения одного важного понятия, которое играет большую роль как в самой теории вероятностей, так и в ее разнообразных применениях, научных и практических. Прежде чем дать формальное определение этого понятия, мы рассмотрим простые примеры.

Пример 1. Бросаются две игральные кости. Событие А состоит в том, что на обеих костях выпадут простые числа очков (2, 3 или 5). Стало известно, что наступило событие В - сумма выпавших очков оказалась четной. Как изменилась вероятность события А от этого дополнительного знания?

Событию А благоприятствуют только следующие 9 исходов: (2,2), (2,3), (2,5), (3,2), (3,3), (3,5), (5,2), (5,3), (5,5). Таким образом, вероятность события А равна

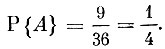
Пусть теперь событие В произошло. Это означает, что должен был наступить какой-то из 18 исходов: (1,1), (1,3), (1,5), (2,2), (2,4), (2,6), (3,1), (3,3), (3,5), (4,2), (4,4), (4,6), (5,1), (5,3), (5,5), (6,2), (6,4), (6,6). Из них пять исходов благоприятствуют и событию А.

Таким образом, вероятность события А при условии, что наступило событие В, равна

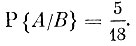
Вероятность Р {А/В} называют условной вероятностью события А при условии, что событие В наступило.

Пример 2. Из урны, содержащей 5 белых и 4 черных шара, наудачу вынимают один вслед за другим два шара. Чему равна вероятность того, что второй шар окажется белым (событие А), если первый шар оказался черным (событие В)? Извлеченный шар в урну не возвращается.

Согласно условию задачи после первого извлечения в урне остались 5 белых и три черных шара. Таким образом, после того как нам стало известно, что событие В наступило, вероятность события А оказывается равной

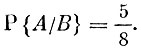
Рассмотренный пример относится к группе задач с из возвращаемыми в урну шарами. Эта схема находит широкие применения на практике, в частности в вопросах, связанных с контролем качества промышленной продукции.

Небольшое изменение условий задачи - вынутый шар немедленно возвращается в урну - приводит к другой важной схеме теории вероятностей - схеме возвращенного шара. В схеме возвращенного шара тот же пример приводит к другому результату. Действительно, узнав, что первый извлеченный шар оказался черным, мы немедленно его возвращаем в урну. Таким образом, перед вторым извлечением в урне снова оказывается 5 белых и 4 черных шара. Таким образом, в этой измененной постановке задачи

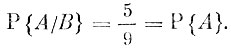
В данном случае условная вероятность оказалась равна вероятности события А без дополнительного условия, т. е. безусловной.

Про событие А говорят, что оно независимо от события В, если наступление события В не изменяет вероятности А, т. е.

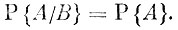(1)

Теперь мы можем перейти к выводу так называемой теоремы умножения вероятностей. Содержание этой теоремы дается следующим равенством

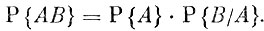(2)

Перейдем к доказательству. Пусть событию А благоприятствуют m равновероятных и несовместимых событий из n всех возможных, событию В - k и событию АВ - l. Предположим для начала, что числа кит отличны от 0. Тогда очевидно, что

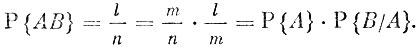
Пояснения, собственно, требует только вычисление одной вероятности, а именно Р {В/А}. Если событие А наступило, то это означает, что произошел какой-то из m исходов, благоприятствующих А. Среди них имеются l исходов, благоприятствующих и событию В. Таким образом, событие В может наступить, если событие А уже наступило, тогда и только тогда, когда произойдет один из этих l исходов, благоприятствующих как А, так и В.

Повторив буквально те же самые рассуждения, можно доказать, что

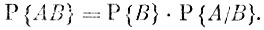(3)

Мы получили теорему умножения в несколько ином виде, в котором события А и В поменялись местами.

Если одно из чисел k или m равно нулю, то проведенное рассуждение уже неверно (на 0 делить нельзя!). Но

этом случае теорема умножения проверяется элементарно.

Действительно, пусть k = 0. Тогда и l = 0; это означает, что Р {В} = Р {А*В} = Р {В/А} = 0. Из этой цепочки равенств вытекают оба равенства (2) и (3).

Теорема доказана полностью.

Предположим теперь, что событие В независимо от А (и, значит, выполнено равенство (1)). Тогда в силу (2) и (3) можно написать равенство Р {А} Р {В} = Р {В}*Р {А/В}. Отсюда, очевидно, находим Р {А/В} = Р {А}. Таким образом, если В независимо от А, то и А независимо от В. Свойство независимости двух событий взаимно, а потому принято говорить, что события А и В независимы, если выполняется хотя бы одно из равенств Р {А/В} = Р {А} или Р {В/А} = Р {В}.

Обратим внимание на то, что для независимых событий А и В теорема умножения записывается особенно просто:

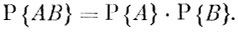
Мы подготовили почву для вывода двух важных формул - формулы полной вероятности и формулы Байеса.

Предположим, что некоторое событие В может произойти только вместе с одним из несовместимых событий А₁, А₂, ..., А_l. Иными словами, событие В можно представить в виде суммы

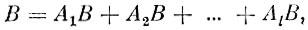
в которой слагаемые являются несовместимыми событиями. В силу теоремы сложения вероятностей

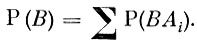
Применив к каждому из слагаемых правой части равенства теорему умножения, получим формулу полной вероятности

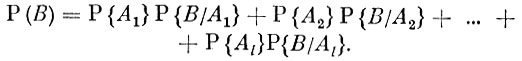(4)

Проиллюстрируем полученную формулу на двух примерах.

Пример 3. Имеются 6 одинаковых урн. В одной из них содержится 2 белых и один черный шар, в двух других - по 3 белых и по 2 черных шара, а в остальных трех - по 2 черных и по одному белому шару. Наудачу вынимается урна, и из нее наудачу вынимается один шар. Чему равна вероятность того, что этот шар окажется белым (событие В)?

Мы находимся в условиях, в которых можно использовать формулу полной вероятности. С этой целью введем три дополнительных события: А₁ - выбранная урна имеет 2 белых и 1 черный шар; А₂ - выбранная урна имеет 3 белых и 2 черных шара; A₃ - выбранная урна содержит 1 белый и 2 черных шара.

Теперь ясно, что

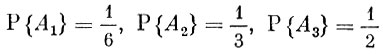
и

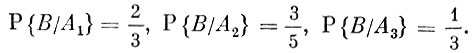
Согласно формуле

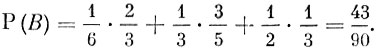
Пример 4. Некоторое изделие вырабатывается на трех заводах. Первый завод изготовляет 100 α % всей продукции, второй - 100 β % и третий - 100 γ % (α + β + γ = 1). Вероятность того, что изделие окажется некачественным, для первого завода равна а, для второго - b и для третьего - с. Потребитель приобрел это изделие в магазине, в который заводы поставляют свою продукцию в тех же пропорциях, в которых они ее изготовляют. Чему равна вероятность, что приобретенное изделие окажется некачественным?

Вновь мы находимся в условиях применимости формулы полной вероятности. Для этого достаточно через В обозначить событие, состоящее в приобретении некачественного изделия, через А₁ - изготовление этого изделия первым заводом, через А₂ - изготовление его вторым и через А₃ - третьим заводом. Согласно условию

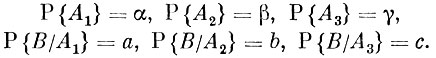
Таким образом,

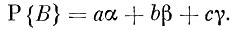
Представим себе теперь, что событие В по-прежнему может произойти только с одним из l несовместимых событий А₁, А₂, ..., А_l. Событие В наступило. Спрашивается, чему равны вероятности того, что оно произошло вместе с событием A_i (i может принять одно из возможных значений - 1, 2, ..., l)?

Согласно теореме умножения

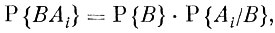
следовательно,

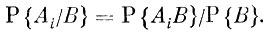
Но

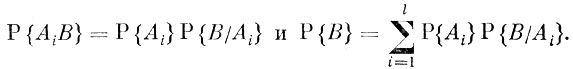
Таким образом,

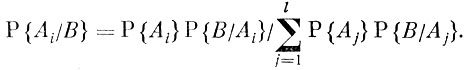(5)

Полученное равенство носит название формулы (формул) Байеса или формулы вероятностей гипотез.

Пример 5. Сохраняются условия примера 3. Вопрос ставится так: из урны был наудачу вынут шар, он оказался белым. Чему равны вероятности того, что шар был вынут из урны первого, второго или третьего состава?

Согласно данным задачи 3 и формуле 5 находим

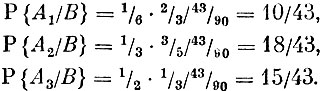
Решенную нами задачу можно истолковать так: у нас имеются три гипотезы - шар вынут из урны первого состава (гипотеза А₁, второго состава (гипотеза А₂), третьего состава (гипотеза А₃), имеющие до опыта вероятности, соответственно равные ¹/₆, ¹/₃, ¹/₂ (доопытные, или априорные вероятности). Произведен опыт (извлечен шар белый), как после опыта изменились вероятности гипотез? Мы видим, что послеопытные (апостериорные) вероятности гипотез несколько отличаются от априорных. С ситуацией, рассмотренной выше, как в научных, так и в практических исследованиях, приходится встречаться постоянно.

Мы рассмотрим еще один пример, заимствованный из многочисленных работ, посвященных автоматическому установлению диагноза заболевания.

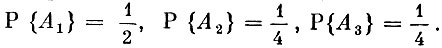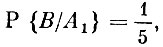
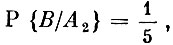
Пример 6. Относительно поступившего на излечение больного имеются подозрения на заболевания А₁ (первая гипотеза), А₂ (вторая гипотеза) и А₃ (третья гипотеза). Согласно проведенным ранее наблюдениям установлено, что С целью уточнения диагноза назначено лабораторное обследование, дающее положительный результат (событие В) для каждого из перечисленных заболеваний с такими вероятностями: 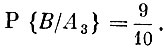Обследование дало положительный результат. Как следует после этого переоценить вероятности заболеваний?

Согласно формуле полной вероятности

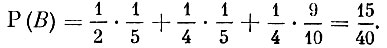
Формулы Байеса теперь дают

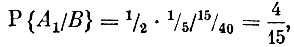
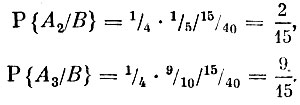
Мы знаем, что врачи у постели больного не считают каждый раз по формулам Байеса, но для уточнения диагноза проводят не по одному, а по нескольку лабораторных исследований. После каждого из таких исследований вероятности заболеваний (гипотез) изменяются, и постепенно вероятность истинного заболевания резко повышается. У нас в примере это произошло с заболеванием А,.